1、备战2020中考数学解题方法专题研究专题8 面积法专题【方法简介】用面积法解几何问题是一种重要的数学方法，在初中数学中有着广泛的应用，这种方法有时显得特别简捷，有出奇制胜、事半功倍之效。所谓面积法，就是利用面积相等或者成比例，来证明其他的线段相等或为成比例线段的方法。有些数学问题，虽然题目中没有直接涉及到面积，借助面积极法不但可证明各种几何图形中的面积等量关系，还可证某些线段相等，角的相等关系以及线段之间的比例式等多种类型的几何题，用面积法证题，关键在于利用题目的特点，分析相应图形面积之间的关系，推出几何题中相应边角关系。【真题演练】1. 如图1，转动转盘，求转盘停止转动时指针指向阴影部分的概
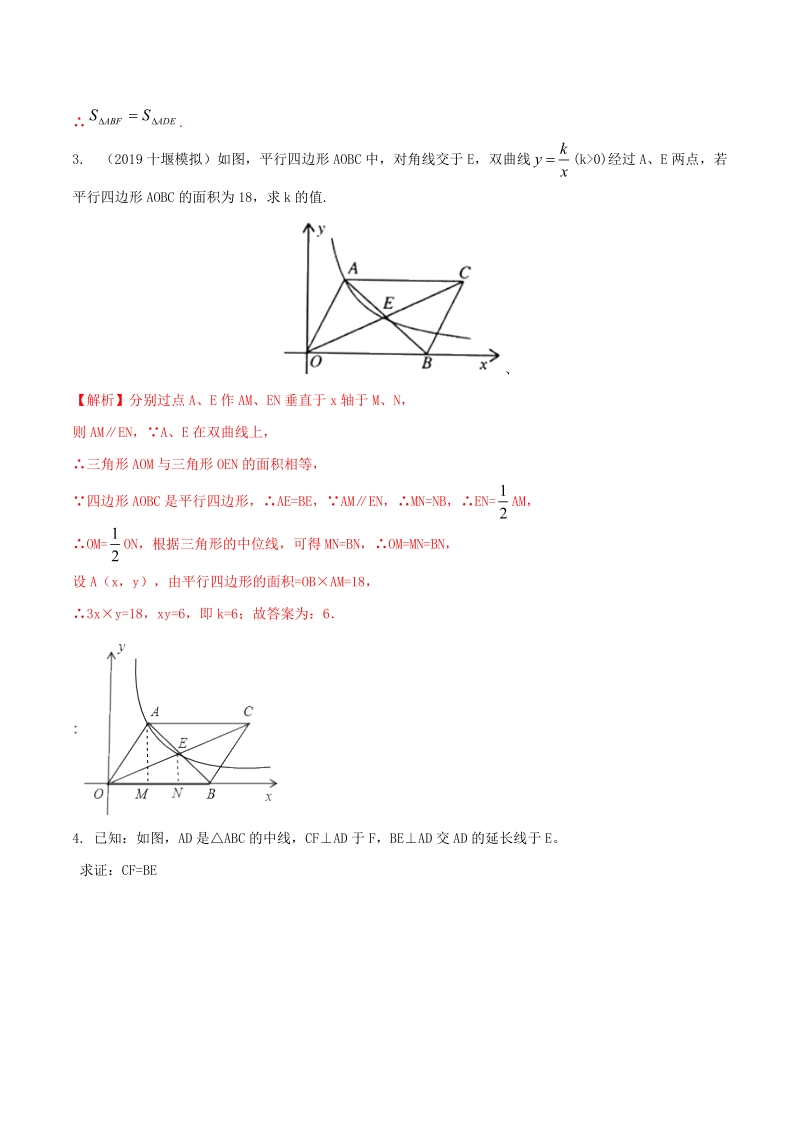
2、率。图1【解析】:观察图1，显然有阴影部分的面积占整个圆面积的一半，故P（阴影部分）=。2. 如图1，过平行四边形的顶点引直线，和、或其延长线分别交于、，求证：.证明：连结,/，又/，.3. （2019十堰模拟）如图，平行四边形AOBC中，对角线交于E，双曲线(k0)经过A、E两点，若平行四边形AOBC的面积为18，求k的值.、【解析】分别过点A、E作AM、EN垂直于x轴于M、N，则AMEN，A、E在双曲线上，三角形AOM与三角形OEN的面积相等，四边形AOBC是平行四边形，AE=BE，AMEN，MN=NB，EN=AM，OM=ON，根据三角形的中位线，可得MN=BN，OM=MN=BN，设A（x
3、，y），由平行四边形的面积=OBAM=18，3xy=18，xy=6，即k=6；故答案为：64. 已知：如图，AD是ABC的中线，CFAD于F，BEAD交AD的延长线于E。求证：CF=BE证明：连结EC，由BD=DC得，两式两边分别相加，得故所以BE=CF。注：直接由得更简洁。【名词释义】平面几何中讲的面积公式以及由面积公式推出的与面积计算有关的性质定理，不仅可用于计算面积，而且用它来证明平面几何题有时会收到事半功倍的效果。运用面积关系来证明或计算平面几何题的方法，称为面积方法，它是几何中的一种常用方法。用归纳法或分析法证明平面几何题，其困难在添置辅助线。面积法的特点是把已知和未知各量用面积公式
4、联系起来，通过运算达到求证的结果。所以用面积法来解几何题，几何元素之间关系变成数量之间的关系，只需要计算，有时可以不添置补助线，即使需要添置辅助线，也很容易考虑到。面积问题主要涉及以下两部分内容：（一）怎样证明面积相等。以下是常用的理论依据1.三角形的中线把三角形分成两个面积相等的部分。2.同底同高或等底等高的两个三角形面积相等。3.平行四边形的对角线把其分成两个面积相等的部分。4.同底（等底）的两个三角形面积的比等于高的比。同高（或等高）的两个三角形面积的比等于底的比。5.三角形的面积等于等底等高的平行四边形的面积的一半。6.三角形的中位线截三角形所得的三角形的面积等于原三角形面积的7.三角
5、形三边中点的连线所成的三角形的面积等于原三角形面积的8.有一个角相等或互补的两个三角形的面积的比等于夹角的两边的乘积的比。（二）用面积法解几何问题（常用的解题思路）1.分解法：通常把一个复杂的图形，分解成几个三角形。2.作平行线法：通过平行线找出同高（或等高）的三角形。3.利用有关性质法：比如利用中点、中位线等的性质。4.还可以利用面积解决其它问题。【典例示例】例题1：如图，C是线段AB上的一点，ACD、BCE都是等边三角形，AE、BD相交于O。求证：AOC=BOC 图6证明：过点C作CPAE，CQBD，垂足分别为P、Q。ACD、BCE都是等边三角形，AC=CD，CE=CB，ACD=BCE，A
6、CE=DCB，ACEDCBAE=BD，可得CP=CQ，OC平分AOB，即AOC=BOC例题2：（2017年湖南 常德）如图2，已知反比例函数y=的图象经过点A（4，m），ABx轴，且AOB的面积为2（1）求k和m的值；（2）若点C（x，y）也在反比例函数y= 图象上，当3x1时，求函数值y的取值范围【解析】：（1）因为AOB的面积为2，根据性质，得k=4，所以反比例函数解析式为y= ，因为A（4，m），所以4m=4,所以m=1；（2）当x=3时，y= ；当x=1时，y=4，因为反比例函数y=在x0时，y随x的增大而减小，所以当3x1时，y的取值范围为4y【归纳总结】(1)等底等高的两个三角形面
7、积相等；(2)等底（或等高）的两三角形面积之比等于其高（或底）之比；(3)在两个三角形中，若两边对应相等，其夹角互补，则这两个三角形面积相等；(4)若在同一线段的同侧有底边相等面积相等的两个三角形，则连结两个三角形的顶点的直线与底边平行。【强化巩固】1. 如图2，在正方形ABCD内任取一点O，连接OA、OB，得ABO，如果正方形ABCD内每一点被取到的可能性都相同，则ABO是钝角三角形的概率是（ ）图2（A）（B） （C） （D）无法确定的【答案】C【解析】：设正方形ABCD的边长为a，则以AB为直径的半圆面积为，所以P（ABO是钝角三角形）=。故选C。2. （2017年辽宁锦州）如图3，矩形
8、OABC中，A（1，0），C（0，2），双曲线y= （0k2）的图象分别交AB，CB于点E，F，连接OE，OF，EF， =2 ,则k值为（）A B1 C D 【答案】A解：因为四边形OABC是矩形，BAOA，A（1，0），所以设E点坐标为（1，k），则F点坐标（ ，2）,则= (1-)(2-k), =,因为A（1，0），C（0，2），所以点B（1,2），所以矩形ABCO的面积为2，所以四边形BFOE的面积为2-k，因为 =2 ,所以= （2-k），所以 （2-k）= (1-)(2-k)，所以k=，所以选A3. （2017年四川阿坝州）如图4，已知点P（6，3），过点P作PMx轴于点M，PNy轴
9、于点N，反比例函数y=的图象交PM于点A，交PN于点B若四边形OAPB的面积为12，则k= 【答案】6【解析】：因为点P（6，3），所以矩形OMPN的面积为18，根据题意，得:k+四边形OAPB的面积=四边形OMPN的面积,所以k=18-12=6，故答案为：64. 如图6，设点P在反比例函数y= 上，PCx轴于点C，交反比例函数y= 的图像于点A，PDy轴于点D，交反比例函数y= 的图像于点B，则四边形PAOB的面积是 .【解析形OCPD的面积是6，三角形OBD和三角形OAC的面积和是2，所以阴影的面积是4.解：填4.5. 已知：如图2，中，点是边上的任意一点，垂足分别为、.猜想：线段、与间的
10、数量关系，并证明.证明：猜想.连接，则，所以，又，有，得.6.已知一直角三角形两直角边为a、b，斜边c上的高为h，求证：证明：由三角形面积关系有即整理后，即得7. 如图1，在RtABC中，C90，AB、BC、CA的长分别为5、3、4求ABC的内切圆半径r【解析】连接OA、OB、OC，则= + + 可得= ，得到r=1.8. 如图3，小红和小明在操场上做游戏，他们先在地上画了半径分别为2m和3m的同心圆，然后蒙上眼睛，并在一定距离外向圈内掷小石子，掷中阴影小红胜，否则小明胜，未掷入圈内（半径为3m的圆内）不算。你认为游戏公平吗？为什么？（1） 游戏结束，小明边走边想：“反过来，能否用频率估计概率
11、的方法，来估算不规则图形的面积呢？”（2）（2）请你设计一个方案，解决这一问题。（要求画出图形，说明设计步骤、原理，并给出计算公式。）【解析】:（1）不公平。因为P（阴影部分）=即小红胜的概率为，小明胜的概率为，所以游戏不公平。（2）可以利用频率估计概率的实验方法估算不规则图形的面积。方案：设计一个可测量面积的规则图形将不规则图形围起来（如面积为S的正方形），如图4所示； 图4向图形中掷点（如蒙上眼向图形中随意掷小石子，掷在图外不记录）；当掷点数充分大（如1万次），记录并统计结果，假设掷入正方形内m次，其中n次掷入不规则图形内；设不规则图形的面积为S1，用频率估计概率，即频率（掷入非规则图形内
12、）概率P（掷入非规则图形内）=，故从而得。9. （2017年辽宁 葫芦岛）如图13，直线y=3x与双曲线y=（k0，且x0）交于点A，点A的横坐标是1（1）求点A的坐标及双曲线的解析式；（2）点B是双曲线上一点，且点B的纵坐标是1，连接OB，AB，求AOB的面积【解析】：（1）把x=1代入y=3x中，得y=3,所以点A的坐标为（1,3），把A(1,3)代入y=中，得k=3,所以反比例函数的解析式为y=；（2）把y=1代入y=中，得x=3，所以点B的坐标为（3,1），如图4所示，过点A作ACy轴，垂足为点C，过点B作BDx轴，垂足为点D，二线交于点E，根据题意，得OD=CE=3,OC=DE=3,
13、所以AE=EB=2,所以=9-3-22=4.10. 小赵对芜湖科技馆有创意的科学方舟形象设计很有兴趣，他回家后将一正五边形纸片延其对称轴对折，如图3（1）.旋转放置，做成科学方舟模型，如图3（2）所示，该正五边形的边心距长为，为科学方舟船头到船底的距离，请你计算的值.(不能用三角函数表达式表示)解：设正五边形的面积为，根据题意知科学方舟的面积为，且，而，即，化简整理得.11. 如图，在平面直角坐标系中，反比例函数y(x0)的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N 两点(1)若点M是AB边的中点，求反比例函数y的解析式和点N的坐标；(2)若AM2，求直线MN的解析式及OMN的面积【解答】解：(1)点M是AB边的中点，M(6，3)反比例函数y经过点M，3.k18.反比例函数的解析式为y.当y6时，x3，N(3，6)(2)由题意，知M(6，2)，N(2，6)设直线MN的解析式为yaxb，则解得直线MN的解析式为yx8.SOMNS正方形OABCSOAMSOCNSBMN3666816.
