1、2019-2020学年四川省自贡市高二（上）期末数学试卷（文科）一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1（5分）一个长方体去掉一个小长方体，所得几何体的正视图与侧（左）视图分别如图所，则该几何体的俯视图为（）ABCD2（5分）从集合a，b的子集中任取1个集合，则这个集合只含有1个元素的概率是（）ABCD3（5分）一次选拔运动员，测得7名选手的身高（单位：cm）分布茎叶图为，记录的平均身高为177cm，有一名候选人的身高记录不清楚，其末位数记为x，那么x的值为（）A4B3C2D14（5分）已知某单位有职工120人，其中男职工90
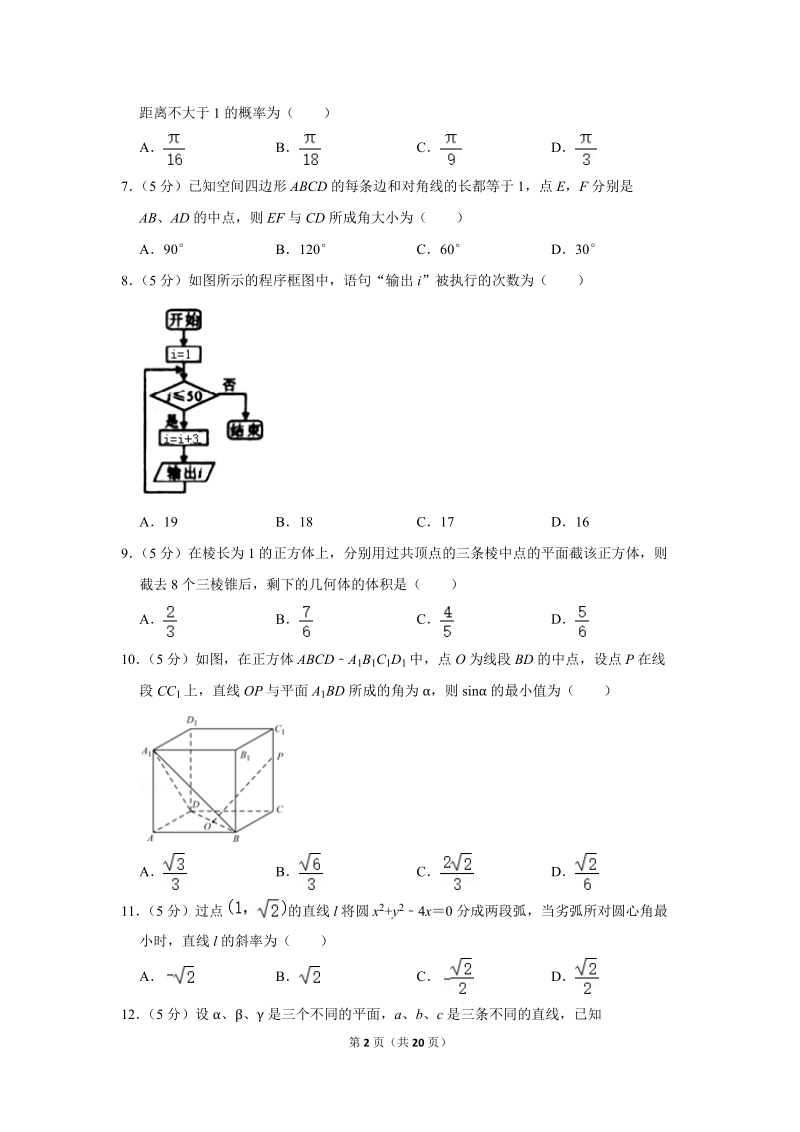
2、人，现采用分层抽样（按男、女分层）抽取一个样本，若样本中有27名男职工，则样本容量为（）A30B36C40D无法确定5（5分）一组数据中的每一个数都减去60，得到一组新数据，若求得新数据的平均数为1.2，方差为4.4，则原来数据的平均数和方差分别为（）A61.2，4.4B58.8，4.4C61.2，64.4D58.8，55.66（5分）在腰长为3的等腰直角三角形内任取一点，使得该点到此三角形的直角顶点的距离不大于1的概率为（）ABCD7（5分）已知空间四边形ABCD的每条边和对角线的长都等于1，点E，F分别是AB、AD的中点，则EF与CD所成角大小为（）A90B120C60D308（5分）如图
3、所示的程序框图中，语句“输出i”被执行的次数为（）A19B18C17D169（5分）在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体，则截去8个三棱锥后，剩下的几何体的体积是（）ABCD10（5分）如图，在正方体ABCDA1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为，则sin的最小值为（）ABCD11（5分）过点的直线l将圆x2+y24x0分成两段弧，当劣弧所对圆心角最小时，直线l的斜率为（）ABCD12（5分）设、是三个不同的平面，a、b、c是三条不同的直线，已知a，b，c给出如下结论：若ab，则bc；若abA，则bcA；若a
4、b，bc，则，；若，则ab，bc其中正确的结论个数是（）A1B2C3D4二、填空题：本大题共4小题，每小题5分，满分20分.13（5分）若B（3，0，4），则|OB| 14（5分）直线m：2x+y5被圆x2+y210截的弦长为 15（5分）某调查机构调查了某地100个新生婴儿的体重，并根据所得数据画出了样本的频率分布直方图（如图所示），则新生婴儿的体重（单位：kg）在3.6，4.4的人数是 16（5分）已知一圆锥的底面直径与母线长相等，一球体与该圆锥的所有母线和底面都相切，则球与圆锥的表面积之比为 三、解答题：本大题共6小题，满分70分，解答须写出文字说明、证明过程或演算步骤.17（10分）如
5、图，正方体ABCDA1B1C1D1中，M，N分别是AB，A1D1的中点判断直线MN与平面BB1D1D的位置关系，并说明理由18（12分）把一个均匀的正方体骰子抛掷两次，观察出现的点数，记第一次出现的点数为a，第二次出现的点数为b，设直线m：2x+y2，直线n：ax+by3（）求直线m和直线n没有交点的概率；（）求直线m和直线n的交点在第一象限的概率19（12分）一束光线通过点M（15，8）射到x轴上经反射后射到圆C：x2+（y7）29上（）求经过圆心的反射光线的方程；（）求反射光线在y轴上截距的范围20（12分）自贡农科所实地考察，研究发现某贫困村适合种植A，B两种药材，可以通过种植这两种药材
6、脱贫通过大量考察研究得到如下统计数据：药材A的亩产量约为300公斤，其收购价格处于上涨趋势，最近五年的价格如下表：编号12345年份20152016201720182019单价（元/公斤）1820232529药材B的收购价格始终为20元/公斤，其亩产量的频率分布直方图如图：（）若药材A的单价y（单位：元/公斤）与年份编号x具有线性相关关系，请求出y关于x的回归直线方程，并估计2020年药材A的单价；（）用上述频率分布直方图估计药材B的平均亩产量，若不考虑其他因素，试判断2020年该村应种植药材A还是药材B？并说明理由参考公式：，（回归方程ybx+a中）21（12分）在等腰梯形ABCD中，ADB
7、C，BC4，AD2，ABC60，将梯形ABCD沿着AB翻折至ABC1D1（如图），使得平面ABCD与平面ABC1D1垂直（）求BC1与AC所成的角的大小；（）求三棱锥BCD1D的体积22（12分）若直线l：xmy2与圆O：x2+y24交于A，B两点，O为原点，ABO的面积为S（）将S表示成m的函数S（m）；（）是否存在实数m使S有最大值2019-2020学年四川省自贡市高二（上）期末数学试卷（文科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1（5分）一个长方体去掉一个小长方体，所得几何体的正视图与侧（左）视图分别
8、如图所，则该几何体的俯视图为（）ABCD【分析】从正视图和侧视图上分析，去掉的长方体的位置应该在的方位，然后判断俯视图的正确图形【解答】解：由正视图可知去掉的长方体在正视线的方向，从侧视图可以看出去掉的长方体在原长方体的左侧，由以上各视图的描述可知其俯视图符合C选项故选：C【点评】本题考查几何体的三视图之间的关系，要注意记忆和理解“长对正、高平齐、宽相等”的含义2（5分）从集合a，b的子集中任取1个集合，则这个集合只含有1个元素的概率是（）ABCD【分析】先列举出集合a，b的所有情况，然后找出符合要求的集合个数，根据古典概率求解公式可求【解答】解：集合a，b的子集有，a，b，a，b共4种情况，
9、集合只含有1个元素的有a，b2种情况，故概率P故选：C【点评】本题主要考查了古典概率的求解公式的简单应用，属于基础试题3（5分）一次选拔运动员，测得7名选手的身高（单位：cm）分布茎叶图为，记录的平均身高为177cm，有一名候选人的身高记录不清楚，其末位数记为x，那么x的值为（）A4B3C2D1【分析】求这7个数的平均数，列出方程，即可解题【解答】解：180+181+170+（170+x）+1177+178+179177；解得x4故选：A【点评】本题以茎叶图为载体，考查平均数，要求会读图属简单题4（5分）已知某单位有职工120人，其中男职工90人，现采用分层抽样（按男、女分层）抽取一个样本，若
10、样本中有27名男职工，则样本容量为（）A30B36C40D无法确定【分析】根据分层抽样的定义和性质进行求解即可【解答】解：设样本容量为n，则由题意得，解得n36，故选：B【点评】本题主要考查分层抽样的应用，根据条件建立比例关系是解决本题的关键5（5分）一组数据中的每一个数都减去60，得到一组新数据，若求得新数据的平均数为1.2，方差为4.4，则原来数据的平均数和方差分别为（）A61.2，4.4B58.8，4.4C61.2，64.4D58.8，55.6【分析】根据题意，由数据的平均数、方差的性质分析可得答案【解答】解：根据题意，若一组数据中的每一个数都减去60，得到一组新数据，若求得新数据的平均
11、数为1.2，方差为4.4，则原来数据的平均数60+1.261.2，方差为4.4；故选：A【点评】本题考查数据的平均数、方差的计算，注意平均数、方差的性质，属于基础题6（5分）在腰长为3的等腰直角三角形内任取一点，使得该点到此三角形的直角顶点的距离不大于1的概率为（）ABCD【分析】求出三角形的面积；再求出据三角形的直角顶点的距离不大于1的区域为扇形，扇形是四分之一圆，求出四分之一圆的面积；利用几何概型概率公式求出该点到此三角形的直角顶点的距离不大于1的概率【解答】解：三角形ABC的面积为S133；到此三角形的直角顶点的距离不大于1的区域是四分之一圆，面积为 S2所以该点到此三角形的直角顶点的距
12、离不大于1的概率是P故选：B【点评】本题考查几何概型的计算，解题的关键是分析满足“到此三角形的直角顶点的距离”的点的性质，得到该区域的面积7（5分）已知空间四边形ABCD的每条边和对角线的长都等于1，点E，F分别是AB、AD的中点，则EF与CD所成角大小为（）A90B120C60D30【分析】由题意作图，连接空间四边形ABCD的对角线AC，BD，根据三角形中位线定理可以推知CDB即为所求的角【解答】解：如图，连接空间四边形ABCD的对角线AC，BD，点E，F分别是AB、AD的中点，EFBD，CDB即为EF与CD所成角由空间四边形ABCD的每条边和对角线的长都等于1，可知底面ABC为等边三角形，
13、故CDB60，故选：C【点评】本题考查两条异面直线所成角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养8（5分）如图所示的程序框图中，语句“输出i”被执行的次数为（）A19B18C17D16【分析】根据框图的流程依次计算运行的结果，判断第n次运行i的值，当满足i50时，求最小的正整数n的值【解答】解：由程序框图知：第一次运行i1+34；第二次运行i1+3+37；第三次运行i1+3+3+310；第n次运行i4+（n1）3当i1+3n50即n17时，程序运行终止，运行的次数为17故选：C【点评】本题考查了循环结构的程序框图，根据框图的流程依次计算运行的结果是解答此类问题的常用方法
14、9（5分）在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体，则截去8个三棱锥后，剩下的几何体的体积是（）ABCD【分析】剩下的几何体的体积，就是正方体的体积求得8个正三棱锥的体积，求出体积差即可【解答】解：由题意几何体的体积，就是正方体的体积求得8个正三棱锥的体积，故选：D【点评】本题考查多面体的体积的求法，考查转化思想，计算能力，是基础题10（5分）如图，在正方体ABCDA1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为，则sin的最小值为（）ABCD【分析】由题意可得：直线OP与平面A1BD所成的角的最小值为AOA1与C1OA1
15、中的最小角再利用正方体的性质和直角三角形的边角关系求解【解答】解：由题意可得：直线OP于平面A1BD所成的角的最小值为AOA1与C1OA1中的最小角不妨取AB2在RtAOA1中，sinAOA1；sinC1OA1sin（2AOA1）sin2AOA12sinAOA1cosAOA12，sin的最小值为故选：B【点评】本题考查了正方体的性质和直角三角形的边角关系、线面角的求法，考查了推理能力，属于中档题11（5分）过点的直线l将圆x2+y24x0分成两段弧，当劣弧所对圆心角最小时，直线l的斜率为（）ABCD【分析】当圆心到直线l的距离最大时，圆心角最小，而 当ACl时，圆心（2，0）到直线的距离最大，
16、根据点到直线的距离公式即可求解【解答】解：圆x2+y24x0可化为（x2）2+y24，圆心C（2，0），半径r2，根据题意可知，当圆心到直线l的距离最大时，圆心角最小，设A（1，）由可知题意直线l的斜率存在，可设直线l：yk（x1），即kxy+0，故当ACl时，圆心（2，0）到直线的距离最大，d，此时直线CA的斜率为，则l的斜率k故选：D【点评】本题主要考查了直线与圆相交性质的应用，解题的关键是把所求角的最值转化为求距离的最值12（5分）设、是三个不同的平面，a、b、c是三条不同的直线，已知a，b，c给出如下结论：若ab，则bc；若abA，则bcA；若ab，bc，则，；若，则ab，bc其中正确
17、的结论个数是（）A1B2C3D4【分析】根据平行和垂直的公理及定理，对四个命题进行一一验证排查，得出正确结果【解答】解：对于，如图，由ab可得b，易证bc，故正确；对于，因为abA，则Aa，Ab，又a，b，AA，c，Ac，即a、b、c三线共点，则正确；对于，a，b，c，a，c，ab，bc，a与c不平行，即a与c相交于一点，b，b，b，故正确；对于，若，b，b，a，c，ab，bc，故正确故选：D【点评】本题考查空间中线线、线面、面面的位置关系，考查空间想象能力，逻辑推理能力，利用平面的性质和定理是解决本题的关键，属于中档题二、填空题：本大题共4小题，每小题5分，满分20分.13（5分）若B（3，
18、0，4），则|OB|5【分析】利用两点间距离公式直接求解【解答】解：B（3，0，4），|OB|5故答案为：5【点评】本题考查两点间距离的求法，考查两点间距离公式等基础知识，考查运算求解能力，是基础题14（5分）直线m：2x+y5被圆x2+y210截的弦长为【分析】利用点到直线距离公式求出圆心到直线的距离，再由垂径定理得答案【解答】解：圆x2+y210的圆心坐标为（0，0），半径r，因为圆心到直线2x+y0的距离d，直线2x+y0被圆x2+y210所截得的弦长222故答案为：2【点评】本题考查直线与圆位置关系的应用，训练了利用垂径定理求弦长，是基础题15（5分）某调查机构调查了某地100个新生婴
19、儿的体重，并根据所得数据画出了样本的频率分布直方图（如图所示），则新生婴儿的体重（单位：kg）在3.6，4.4的人数是20【分析】求出3.6，4.4的概率，再求出即可【解答】解：根据图象，新生婴儿的体重（单位：kg）在3.6，4.4的概率为0.4（0.375+0.125）0.2，由1000.220，故答案为：20【点评】考查频率分布直方图求概率，样本估计总体，基础题16（5分）已知一圆锥的底面直径与母线长相等，一球体与该圆锥的所有母线和底面都相切，则球与圆锥的表面积之比为【分析】设底面圆的半径和内切球的半径，由题意可得两个半径的关系，进而求出表面积之比【解答】解：画出轴截面，则BC为底面圆的直
20、径，底面半径设为R，OE为内切球的半径设R，OEAC，ADBC由题意知：AC2R，DCR，tan30，ODR，S球4R2，S锥S底+S侧R2+3R2，所以球与圆锥的表面积之比：，故答案为：，【点评】考查圆锥和球的表面积公式，属于中档题三、解答题：本大题共6小题，满分70分，解答须写出文字说明、证明过程或演算步骤.17（10分）如图，正方体ABCDA1B1C1D1中，M，N分别是AB，A1D1的中点判断直线MN与平面BB1D1D的位置关系，并说明理由【分析】MN平面BB1D1D，取AD中点E，连接ME，NE，推导出MEBD，NED1D，从而平面EMN平面BB1D1D，由此能证明MN平面BB1D1
21、D【解答】解：MN平面BB1D1D，取AD中点E，连接ME，NE，根据题知MEBD，NED1D，所以平面EMN平面BB1D1D，因为MN平面EMN，故MN平面BB1D1D【点评】本题考查线面位置关系的判断与求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题18（12分）把一个均匀的正方体骰子抛掷两次，观察出现的点数，记第一次出现的点数为a，第二次出现的点数为b，设直线m：2x+y2，直线n：ax+by3（）求直线m和直线n没有交点的概率；（）求直线m和直线n的交点在第一象限的概率【分析】利用列举法得到同时向上掷两枚骰子，向上的点数之和共有36种结果，（I）根据直
22、线平行的条件可转化为a2b，找出符合条件的可能情况，然后结合古典概率求解公式即可求解；（II）联立直线，求出满足条件的交点坐标，即可求出满足题意的（m，n）的数目，根据古典概率的求解公式即可求解【解答】解：骰子抛掷两次的结果记为（a，b），则有（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），（2，1），（2，2），（2，3），（2，4），（2，5），（2，6），（3，1），（3，2），（3，3），（3，4），（3，5），（3，6），（4，1），（4，2），（4，3），（4，4），（4，5），（4，6），（5，1），（5，2），（5，3），（5，4），（5，5），（5，6
23、）（6，1），（6，2），（6，3），（6，4），（6，5），（6，6）共36种不同的结果（）直线m和直线n没有交点即mn，所以a2b，共有（2，1），（4，2），（6，3）3种不同结果因此所求概率（）得，由得或者，有（4，1），（5，1），（6，1），（1，2），（1，3），（1，4），（1，5），（1，6），（2，2），（2，3），（2，4），（2，5），（2，6）共13种不同结果因此所求概率【点评】本题考查概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用19（12分）一束光线通过点M（15，8）射到x轴上经反射后射到圆C：x2+（y7）29上（）求经过圆心的反射光线的方程；（
24、）求反射光线在y轴上截距的范围【分析】（）根据题意，分析可得反射光线经过点（15，8）和（0，7），进而分析可得答案；（）根据题意，分反射光线的斜率是否存在两种情况讨论：反射光线的斜率不存在，即反射光线的方程为15，分析其与圆的关系可得结论，反射光线的斜率存在，不妨设反射光线所在直线方程为y+8k（x15），由直线与圆的位置关系可得，解可得k的范围，即可得答案【解答】解：（）根据题意，由光学原理可得：一束光线通过点M（15，8）射到x轴上，经反射后的反射光线经过N（15，8）圆Cx2+（y7）29的圆心为（0，7），则反射光线经过点（15，8）和（0，7）；则反射光线的方程：，即yx+7；（）
25、根据题意，分2种情况讨论：，反射光线的斜率不存在，即反射光线的方程为15，与圆C不相交，不符合条件，反射光线的斜率存在，不妨设反射光线所在直线方程为y+8k（x15），即kxy15k80，由已知得，即12k2+25k+120，故方程kxy15k80中，令x0得反射光线在y轴上截距，因此反射光线在y轴上截距b的范围为【点评】本题考查直线与圆的位置关系，涉及直线的对称问题，属于基础题20（12分）自贡农科所实地考察，研究发现某贫困村适合种植A，B两种药材，可以通过种植这两种药材脱贫通过大量考察研究得到如下统计数据：药材A的亩产量约为300公斤，其收购价格处于上涨趋势，最近五年的价格如下表：编号12
26、345年份20152016201720182019单价（元/公斤）1820232529药材B的收购价格始终为20元/公斤，其亩产量的频率分布直方图如图：（）若药材A的单价y（单位：元/公斤）与年份编号x具有线性相关关系，请求出y关于x的回归直线方程，并估计2020年药材A的单价；（）用上述频率分布直方图估计药材B的平均亩产量，若不考虑其他因素，试判断2020年该村应种植药材A还是药材B？并说明理由参考公式：，（回归方程ybx+a中）【分析】（I）求出线性回归方程，把x6代入即可；（II）先求出430450的的值，再求出B的平均值，再求出B的产值，根据（I）求出A的产值，比较求出即可【解答】解：
27、（I），a，所以线性回归方程为y2.7x+14.9，当x6时，y31.1，因此估计2020年药材A的单价为31.1元/公斤；（II）设430450这一组的的值为a，利用概率和为1，所以0.00520+0.01020+0.017520+0.012520+a201，得到a0.005，所以B药材的亩产量的平均值为3600.00520+3800.01020+4000.017520+4200.012520+4400.00520401，由（1）A药材产值为30031.19330（元），B药材产值为204018020（元）故应该种植A种药材【点评】考查求线性回归方程和线性回归方程的应用，频率分布直方图求概率
28、，平均值等，中档题21（12分）在等腰梯形ABCD中，ADBC，BC4，AD2，ABC60，将梯形ABCD沿着AB翻折至ABC1D1（如图），使得平面ABCD与平面ABC1D1垂直（）求BC1与AC所成的角的大小；（）求三棱锥BCD1D的体积【分析】（）推导出ABAC，从而AC平面ABC1D1，进而BC1AC，由此能求出BC1与AC所成的角（）三棱锥BCD1D的体积为由此能求出结果【解答】解：（）在等腰梯形中过A作BC垂线交BC于E，由BC2，AD4，则，所以AB2+AC2BC2，所以ABAC，又因为平面ABCD与平面ABC1D1垂直，所以AC平面ABC1D1，所以BC1AC，BC1与AC所成
29、的角为（）三棱锥BCD1D的体积为：【点评】本题考查异面直线所成角的求法，考查三棱锥的体积求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题22（12分）若直线l：xmy2与圆O：x2+y24交于A，B两点，O为原点，ABO的面积为S（）将S表示成m的函数S（m）；（）是否存在实数m使S有最大值【分析】（）圆心O到直线l：的距离，求出AB，然后求解三角形的面积表达式（）令t1+m2，利用二次函数的性质，求解函数的最值即可【解答】解：（）圆心O到直线l：的距离，弦（）令t1+m2，所以，因此t1+m24，即存在，S的最大值为2【点评】本题考查直线与圆的位置关系的综合应用，三角形的面积的最值的求法，考查转化思想以及计算能力，是中档题
