1、2018-2019学年四川省成都市高二（上）期末数学试卷（理科）一、选择题：本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的1（5分）如图是某班篮球队队员身高（单位：厘米）的茎叶图，则该篮球队队员身高的众数是（）A168B181C186D1912（5分）命题“若ab，则a2b2”的逆否命题是（）A若a2b2，则ab，B若ab，则a2b2C若a2b2，则abD若ab，则a2b23（5分）已知抛物线C的顶点在坐标原点焦点F在x轴上，且抛物线C上横坐标为4的点P到焦点F的距离为5，则抛物线C的标准方程是（）Ay28xBy24xCy22xDy2x4（5分）在一次
2、摸取奖票的活动中，已知中奖的概率为2%，若票仓中有足够多的票则下列说法正确的是（）A若只摸取一张票，则中奖的概率为1%B若只摸取一张票，则中奖的概率为2%C若100个人按先后顺序每人摸取1张票则一定有2人中奖D若100个人按先后顺序每人摸取1张票，则第一个摸票的人中奖概率最大5（5分）阅读如图所示的算法语句如果输入的A，B的值分别为1，2，那么输出的A，B的值分别为（）A1，1B2，2C1，2D2，16（5分）已知数据x1，x2，x3的方差s24，则x1+2，x2+2，x3+2的方差为（）A4B6C16D367（5分）如图是某超市一年中各月份的收入与支出（单位：万元）情况的条形统计图已知利润为
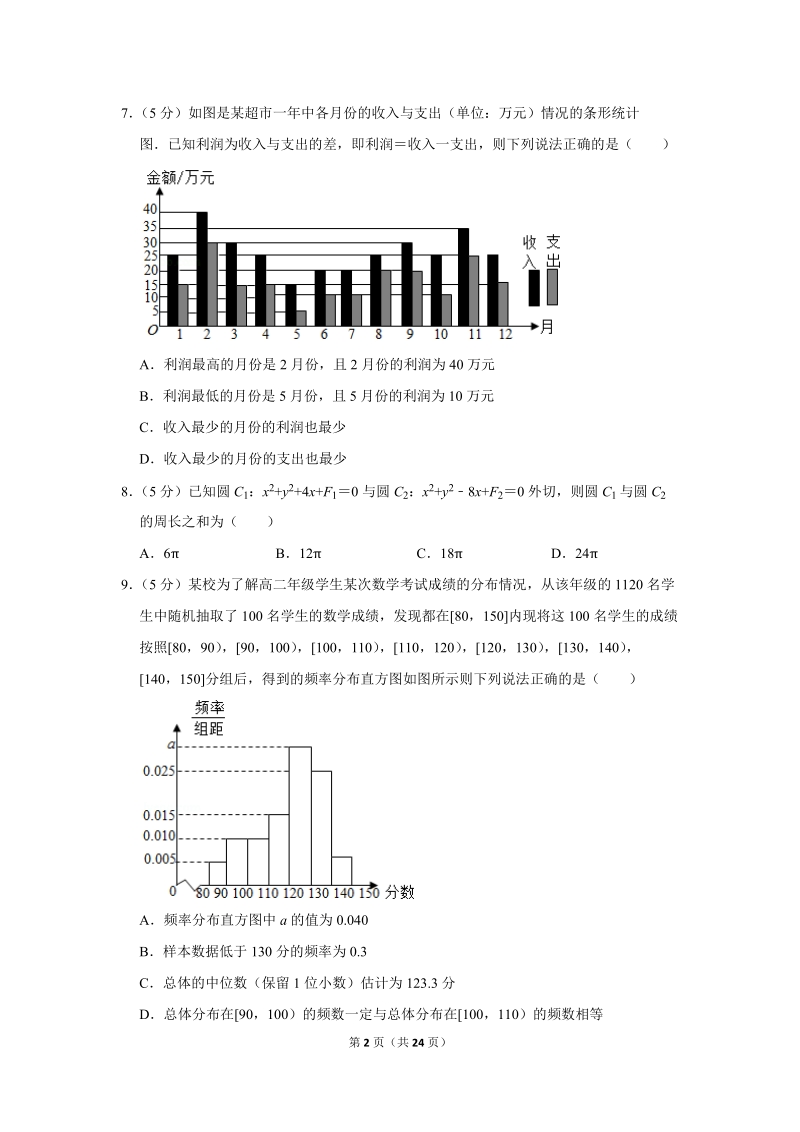
3、收入与支出的差，即利润收入一支出，则下列说法正确的是（）A利润最高的月份是2月份，且2月份的利润为40万元B利润最低的月份是5月份，且5月份的利润为10万元C收入最少的月份的利润也最少D收入最少的月份的支出也最少8（5分）已知圆C1：x2+y2+4x+F10与圆C2：x2+y28x+F20外切，则圆C1与圆C2的周长之和为（）A6B12C18D249（5分）某校为了解高二年级学生某次数学考试成绩的分布情况，从该年级的1120名学生中随机抽取了100名学生的数学成绩，发现都在80，150内现将这100名学生的成绩按照80，90），90，100），100，110），110，120），120，130
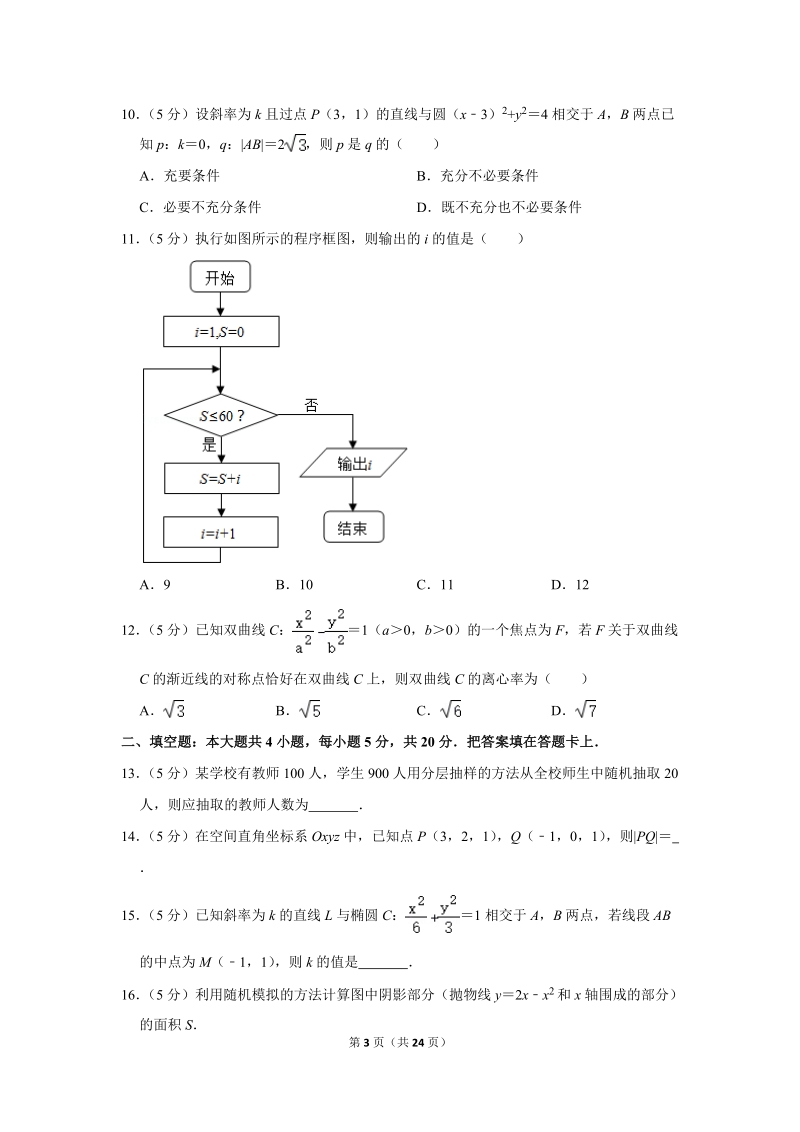
4、），130，140），140，150分组后，得到的频率分布直方图如图所示则下列说法正确的是（）A频率分布直方图中a的值为0.040B样本数据低于130分的频率为0.3C总体的中位数（保留1位小数）估计为123.3分D总体分布在90，100）的频数一定与总体分布在100，110）的频数相等10（5分）设斜率为k且过点P（3，1）的直线与圆（x3）2+y24相交于A，B两点已知p：k0，q：|AB|2，则p是q的（）A充要条件B充分不必要条件C必要不充分条件D既不充分也不必要条件11（5分）执行如图所示的程序框图，则输出的i的值是（）A9B10C11D1212（5分）已知双曲线C：1（a0，b0）
5、的一个焦点为F，若F关于双曲线C的渐近线的对称点恰好在双曲线C上，则双曲线C的离心率为（）ABCD二、填空题：本大题共4小题，每小题5分，共20分把答案填在答题卡上13（5分）某学校有教师100人，学生900人用分层抽样的方法从全校师生中随机抽取20人，则应抽取的教师人数为 14（5分）在空间直角坐标系Oxyz中，已知点P（3，2，1），Q（1，0，1），则|PQ| 15（5分）已知斜率为k的直线L与椭圆C：1相交于A，B两点，若线段AB的中点为M（1，1），则k的值是 16（5分）利用随机模拟的方法计算图中阴影部分（抛物线y2xx2和x轴围成的部分）的面积S第一步，利用计算机产生两组01区间
6、的均匀随机数；a1RAND，b1RAND第二步，进行伸缩变换a2a1，b2b1；第三步，数出落在阴影内的样本点数N1现做了100次试验，模拟得到N131，由此估计S 三、解答题：本大题共6小题，共70分解答应写出文字说明证明过程或演算步骤17（10分）某车间有5名工人其中初级工2人，中级工2人，高级工1人现从这5名工人中随机抽取2名（）求被抽取的2名工人都是初级工的概率；（）求被抽取的2名工人中没有中级工的概率18（12分）已知点A（1，2），B（2，1），C（2，3）在圆E上，过点P（1，0）的直线l与圆E相切（）求圆E的方程；（）求直线l的方程19（12分）已知mR，p：xR，x2mx+1
7、0，g：指数函数ymx（m0，且m1）在R上单调递增（）若pq是真命题，求m的取值范围；（）在（）的条件下，求椭圆1的离心率e的取值范围20（12分）已知椭圆C的焦点为F1（1，0），F2（1，0），点P（1，）在椭圆C上（）求椭圆C的标准方程；（）若斜率为的直线l与椭圆C相交于A，B两点，点Q满足，求ABQ面积的最大值21（12分）保部门研究发现某地的PM10浓度与车流量之间有线性相关关系现采集到该地一周内车流量x与PM10浓度y的数据如表：时间车流量x （单位：万辆）PM10浓度y（单位：g/m3）星期一25.435.7星期二24.634.5星期三23.535.2星期四24.433.6星期
8、五25.836.1星期六19.730.9星期日20.329.4（）在如图所示的坐标系中作出表中数据的散点图；（）根据表中统计数据，求出线性回归方程x+（计算b时精确到0.01，计算a时精确到0.01）；（）为净化空气，该地决定下周起在工作日（星期一至星期五）限号假设限号时每个工作日的车流量为表中对应工作日的，试预测下周星期三的PM10浓度（精确到0.1）参考公式：，参考数据23.4，33.6，（xi）（yi）34.5，x35.522（12分）设p0，动圆C经过点M（p，0），且被y轴截得的弦长为2p，记动圆圆心C的轨迹为E（）求轨迹E的方程；（）求证：在轨迹E上存在点A，B，使得OAB（O为坐
9、标原点）是以A为直角顶点的等腰直角三角形2018-2019学年四川省成都市高二（上）期末数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的1（5分）如图是某班篮球队队员身高（单位：厘米）的茎叶图，则该篮球队队员身高的众数是（）A168B181C186D191【分析】利用茎叶图能求出该篮球队队员身高的众数【解答】解：如图是某班篮球队队员身高（单位：厘米）的茎叶图，则该篮球队队员身高的众数是186故选：C【点评】本题考查众数的求法，考查茎叶图的性质等基础知识，考查运算求解能力，考查数形结合思想，是基础题2（5分）命
10、题“若ab，则a2b2”的逆否命题是（）A若a2b2，则ab，B若ab，则a2b2C若a2b2，则abD若ab，则a2b2【分析】根据命题“若p，则q”的逆否命题是“若q，则p”，写出即可【解答】解：命题“若ab，则a2b2”，它的逆否命题是“若a2b2，则ab”故选：C【点评】本题考查了四种命题之间的关系与应用问题，是基础题3（5分）已知抛物线C的顶点在坐标原点焦点F在x轴上，且抛物线C上横坐标为4的点P到焦点F的距离为5，则抛物线C的标准方程是（）Ay28xBy24xCy22xDy2x【分析】由题意可设抛物线的方程为y22px（p0），求得准线方程，由抛物线的定义可得p的方程，解方程即可得
11、到所求抛物线方程【解答】解：由题意可设抛物线的方程为y22px（p0），可得抛物线的准线方程为x，由抛物线的定义可得抛物线C上横坐标为4的点P到焦点F的距离为5，即为4+5，解得p2，则抛物线的方程为y24x故选：B【点评】本题考查抛物线的定义、方程和性质，注意定义法的运用，以及待定系数法，考查运算能力，属于基础题4（5分）在一次摸取奖票的活动中，已知中奖的概率为2%，若票仓中有足够多的票则下列说法正确的是（）A若只摸取一张票，则中奖的概率为1%B若只摸取一张票，则中奖的概率为2%C若100个人按先后顺序每人摸取1张票则一定有2人中奖D若100个人按先后顺序每人摸取1张票，则第一个摸票的人中奖
12、概率最大【分析】利用概率的定义和性质直接求解【解答】解：在一次摸取奖票的活动中，已知中奖的概率为2%，在A中，若只摸取一张票，则中奖的概率为2%，故A 错误；在B中，若只摸取一张票，则中奖的概率为1%，故B正确；在C中，若100个人按先后顺序每人摸取1张票，不一定有2人中奖，故C错误；在D中，若100个人按先后顺序每人摸取1张票，则第一个摸票的人中奖概率都是2%，故D错误故选：B【点评】本题考查命题真假的判断，考查概率定义、性质等基础知识，考查运算求解能力，是基础题5（5分）阅读如图所示的算法语句如果输入的A，B的值分别为1，2，那么输出的A，B的值分别为（）A1，1B2，2C1，2D2，1【
13、分析】模拟程序的运行，根据赋值语句的功能即可得解【解答】解：模拟程序的运行，可得A1，B2x1，A2，B1输出A的值为2，B的值为1故选：D【点评】本题考查了程序语言的应用问题，考查了对应思想的应用，属于基础题6（5分）已知数据x1，x2，x3的方差s24，则x1+2，x2+2，x3+2的方差为（）A4B6C16D36【分析】利用方差的性质直接求解【解答】解：数据x1，x2，x3的方差S24，x1+2，x2+2，x3+2的方差为12S24故选：A【点评】本题考查方差的求法，考查方差的性质等基础知识，考查运算求解能力，考查数形结合思想，是基础题7（5分）如图是某超市一年中各月份的收入与支出（单位
14、：万元）情况的条形统计图已知利润为收入与支出的差，即利润收入一支出，则下列说法正确的是（）A利润最高的月份是2月份，且2月份的利润为40万元B利润最低的月份是5月份，且5月份的利润为10万元C收入最少的月份的利润也最少D收入最少的月份的支出也最少【分析】利用收入与支出（单位：万元）情况的条形统计图直接求解【解答】解：在A中，利润最高的月份是3月份，且2月份的利润为15万元，故A错误；在B中，利润最小的月份是8月份，且8月分的利润为5万元，故B错误；在C中，收入最少的月份是5月份，但5月份的支出也最少，故5月分的利润不是最少，故C错误；在D中，收入最少的月份是5月份，但5月份的支出也最少，故D正
15、确故选：D【点评】本题考查命题真假的判断，考查收入与支出（单位：万元）情况的条形统计图的性质等基础知识，考查运算求解能力，考查数形结合思想，是基础题8（5分）已知圆C1：x2+y2+4x+F10与圆C2：x2+y28x+F20外切，则圆C1与圆C2的周长之和为（）A6B12C18D24【分析】利用配方法求出利用的标准方程，求出圆心坐标，利用外切关系求出两圆的半径之和，结合圆的周长公式进行计算即可【解答】解：两圆的标准方程为圆C1：（x+2）2+y24F1，圆C2：（x4）2+y216F2，两圆的圆心为C1（2，0），C2（4，0），则两圆外切，两圆半径之和R+r|C1C2|24|6，则圆C1与
16、圆C2的周长之和2R+2r2（R+r）12，故选：B【点评】本题主要考查圆的周长的计算，可以圆与圆的位置关系，利用配方法求出圆心坐标是解决本题的关键9（5分）某校为了解高二年级学生某次数学考试成绩的分布情况，从该年级的1120名学生中随机抽取了100名学生的数学成绩，发现都在80，150内现将这100名学生的成绩按照80，90），90，100），100，110），110，120），120，130），130，140），140，150分组后，得到的频率分布直方图如图所示则下列说法正确的是（）A频率分布直方图中a的值为0.040B样本数据低于130分的频率为0.3C总体的中位数（保留1位小数）估计为
17、123.3分D总体分布在90，100）的频数一定与总体分布在100，110）的频数相等【分析】由频率分布直方图得的性质求出a0.030；样本数据低于130分的频率为：1（0.025+0.005）100.7；80，120）的频率为0.4，120，130）的频率为0.3由此求出总体的中位数（保留1位小数）估计为：120+123.3分；样本分布在90，100）的频数一定与样本分布在100，110）的频数相等，总体分布在90，100）的频数不一定与总体分布在100，110）的频数相等【解答】解：由频率分布直方图得：（0.005+0.010+0.010+0.015+a+0.025+0.005）101，解
18、得a0.030，故A错误；样本数据低于130分的频率为：1（0.025+0.005）100.7，故B错误；80，120）的频率为：（0.005+0.010+0.010+0.015）100.4，120，130）的频率为：0.030100.3总体的中位数（保留1位小数）估计为：120+123.3分，故C正确；样本分布在90，100）的频数一定与样本分布在100，110）的频数相等，总体分布在90，100）的频数不一定与总体分布在100，110）的频数相等，故D错误故选：C【点评】本题考查命题真假的判断，考查频率分布直方图的性质等基础知识，考查运算求解能力，考查数形结合思想，是基础题10（5分）设斜
19、率为k且过点P（3，1）的直线与圆（x3）2+y24相交于A，B两点已知p：k0，q：|AB|2，则p是q的（）A充要条件B充分不必要条件C必要不充分条件D既不充分也不必要条件【分析】设出直线方程，求出圆心和半径，利用直线和圆相交的弦长公式建立方程进行求解，结合充分条件和必要条件的定义进行判断即可【解答】解：斜率为k且过点P（3，1）的直线方程为y1k（x3），即kxy+13k0，圆心（3，0）到直线的距离d，圆的半径R2，若|AB|2，则，即4+3，则1，即1+k21，得k0，即p是q的充要条件，故选：A【点评】本题主要考查充分条件和必要条件的判断，结合直线和圆相交的弦长公式是解决本题的关键
20、11（5分）执行如图所示的程序框图，则输出的i的值是（）A9B10C11D12【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算S的值并输出变量i的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案【解答】解：模拟程序的运行，可得i1，S0满足条件S60，执行循环体，S1，i2满足条件S60，执行循环体，S3，i3满足条件S60，执行循环体，S6，i4满足条件S60，执行循环体，S10，i5满足条件S60，执行循环体，S15，i6满足条件S60，执行循环体，S21，i7满足条件S60，执行循环体，S28，i8满足条件S60，执行循环体，S36，i9满足条件S60，执行循
21、环体，S45，i10满足条件S60，执行循环体，S55，i11满足条件S60，执行循环体，S66，i12此时，不满足条件S60，退出循环，输出i的值为12故选：D【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题12（5分）已知双曲线C：1（a0，b0）的一个焦点为F，若F关于双曲线C的渐近线的对称点恰好在双曲线C上，则双曲线C的离心率为（）ABCD【分析】设F（c，0），渐近线方程为yx，对称点为F（m，n），运用中点坐标公式和两直线垂直的条件：斜率之积为1，求出对称点的坐标，代入双曲线的方程，由离心率公式计算即可得到所求值【解答】解：设F（c
22、，0），渐近线方程为yx，对称点为F（m，n），即有，且n，解得m，n，将F（，），即（，），代入双曲线的方程可得1，化简可得41，即有e25，解得e故选：B【点评】本题考查双曲线的离心率的求法，注意运用中点坐标公式和两直线垂直的条件：斜率之积为1，以及点满足双曲线的方程，考查化简整理的运算能力，属于中档题二、填空题：本大题共4小题，每小题5分，共20分把答案填在答题卡上13（5分）某学校有教师100人，学生900人用分层抽样的方法从全校师生中随机抽取20人，则应抽取的教师人数为2【分析】先求出每个个体被抽到的概率，再用教师的人数乘以此概率，即得所求【解答】解：每个个体被抽到的概率等于，则应抽
23、取的教师人数为1002，故答案为：2【点评】本题主要考查分层抽样的定义和方法，用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数，属于基础题14（5分）在空间直角坐标系Oxyz中，已知点P（3，2，1），Q（1，0，1），则|PQ|2【分析】利用空间中两点间距离公式直接求解【解答】解：在空间直角坐标系Oxyz中，点P（3，2，1），Q（1，0，1），|PQ|2故答案为：2【点评】本题考查两点间的距离的求法，考查两点间距离公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题15（5分）已知斜率为k的直线L与椭圆C：1相交于A，B两点，若线段AB的中点为M（1，1），则k的值是
24、【分析】通过直线l过点M（1，1）可设其方程为xm（y1）+1，并与椭圆方程联立，利用韦达定理及中点坐标公式计算即得直线方程，得到直线的斜率k【解答】解：依题意，设直线l方程为：xm（y1）1，联立，消去x整理得：（2+m2）y22m（m+1）y+m2+2m50，设A（x1，y1），B（x2，y2），则y1+y2，且线段AB的中点为M（1，1），2，即m2直线l方程为x2（y1）1，即x2y+30，所以直线的斜率k为：故答案为：【点评】本题考查直线与圆锥曲线的关系，考查运算求解能力，注意解题方法的积累，属于中档题16（5分）利用随机模拟的方法计算图中阴影部分（抛物线y2xx2和x轴围成的部分）
25、的面积S第一步，利用计算机产生两组01区间的均匀随机数；a1RAND，b1RAND第二步，进行伸缩变换a2a1，b2b1；第三步，数出落在阴影内的样本点数N1现做了100次试验，模拟得到N131，由此估计S1.24【分析】由计算器做模拟试验结果试验估计，得出点落在阴影部分的概率，再转化为几何概型的面积类型求解阴影部分的面积【解答】解：根据题意：点落在阴影部分的点的概率是，矩形的面积为224，阴影部分的面积为S，则有 ，S1.24故答案为：1.24【点评】本题考查了模拟方法估计概率以及几何概型中面积类型的概率问题，是基础题三、解答题：本大题共6小题，共70分解答应写出文字说明证明过程或演算步骤1
26、7（10分）某车间有5名工人其中初级工2人，中级工2人，高级工1人现从这5名工人中随机抽取2名（）求被抽取的2名工人都是初级工的概率；（）求被抽取的2名工人中没有中级工的概率【分析】（）设初级工为a1，a2，中级工为b1，b2，高级工为c，从中随机取2人，利用列举法能求出被抽取的2名工人都是初级工的概率（）利用列举法求出没有抽取中级工的情况有3种，由此能求出被抽取的2名工人中没有中级工的概率【解答】解：（）设初级工为a1，a2，中级工为b1，b2，高级工为c，从中随机取2人，基本事件有10个，分别为：（a1，a2），（a1，b1），（a1，b2），（a1，c），（a2，b1），（a2，b2），
27、（a2，c），（b1，b2），（b1，c），（b2，c）抽到2名工人都是初级工的情况为：（a1，a2），共1种，被抽取的2名工人都是初级工的概率p（）没有抽取中级工的情况有3种，分别为：（a1，a2），（a1，c），（a2，c），被抽取的2名工人中没有中级工的概率p【点评】本题考查概率的求法，考查古典概型等基础知识，考查运算求解能力，是基础题18（12分）已知点A（1，2），B（2，1），C（2，3）在圆E上，过点P（1，0）的直线l与圆E相切（）求圆E的方程；（）求直线l的方程【分析】（）根据题意，设圆E的圆心为（a，b），半径为r；将A、B、C三点的坐标代入圆E的方程可得，解可得，即可得圆
28、E的方程；（）根据题意，分2种情况讨论：，当直线l的斜率不存在时，直线l的方程为x1，验证可得此时符合题意，当直线l的斜率存在时，设直线l的方程为yk（x1），即kxyk0，由直线与圆的位置关系计算可得k的值，可得此时直线的方程，综合即可得答案【解答】解：（）根据题意，设圆E的圆心为（a，b），半径为r；则圆E的方程为（xa）2+（yb）2r2，又由点A（1，2），B（2，1），C（2，3）在圆E上，则有，解可得，即圆E的方程为（x2）2+（y2）21；（）根据题意，分2种情况讨论：，当直线l的斜率不存在时，直线l的方程为x1，与圆M相切，符合题意；，当直线l的斜率存在时，设直线l的方程为yk
29、（x1），即kxyk0，圆心E到直线l的距离d1，解可得k，则直线l的方程为y（x1），即3x4y30，综合可得：直线l的方程为x1或3x4y30【点评】本题考查直线与圆方程的应用，涉及圆的标准方程以及切线方程的计算，属于基础题19（12分）已知mR，p：xR，x2mx+10，g：指数函数ymx（m0，且m1）在R上单调递增（）若pq是真命题，求m的取值范围；（）在（）的条件下，求椭圆1的离心率e的取值范围【分析】（）由pq是真命题，可知p，q都是真命题，当p为真命题时，解得m的范围，当q为真命题时，求出m的范围，取交集即可求出m的取值范围；（）由（）知，1m2，结合椭圆的性质，可得，再由函数
30、在（1，2上单调递增，即可求出椭圆离心率e的取值范围【解答】解：（）pq是真命题，p，q都是真命题当p为真命题时，x2mx+10，则m240，解得2m2当q为真命题时，m1m的取值范围是m|1m2；（）由（）知，1m2，1m2，而函数在（1，2上单调递增，该椭圆离心率e的取值范围是（，【点评】本题考查了复合命题的真假判断，考查了不等式的解法以及函数的单调性，是中档题20（12分）已知椭圆C的焦点为F1（1，0），F2（1，0），点P（1，）在椭圆C上（）求椭圆C的标准方程；（）若斜率为的直线l与椭圆C相交于A，B两点，点Q满足，求ABQ面积的最大值【分析】（）设椭圆C的标准方程为1（ab0），
31、由椭圆C的焦点为F1（1，0），F2（1，0），点P（1，）在椭圆C上，列方程组求出a2，b，由此能求出椭圆C的标准方程（）设直线l：y+m，联立，得x2+mx+m230，由此利用根的判别式、韦达定理、弦长公式、点到直线的距离公式，能求出ABQ面积的最大值【解答】解：（）设椭圆C的标准方程为1（ab0），椭圆C的焦点为F1（1，0），F2（1，0），点P（1，）在椭圆C上，解得a2，b，椭圆C的标准方程为1（）设直线l：y+m，A（x1，y1），B（x2，y2），联立，消去y，得x2+mx+m230，由m24（m23）3（4m2）0，解得2m2，|AB|，由2，知Q（1，），点Q到直线l的距离
32、为d，ABQ的面积S|AB|d，当且仅当m时，SABQ面积的最大值为【点评】本题考查椭圆方程的求法，考查三角形面积的最大值的求法，考查椭圆、直线方程、根的判别式、韦达定理、弦长公式、点到直线的距离公式等基础知识，考查运算求解能力、推理论证能力，是中档题21（12分）保部门研究发现某地的PM10浓度与车流量之间有线性相关关系现采集到该地一周内车流量x与PM10浓度y的数据如表：时间车流量x （单位：万辆）PM10浓度y（单位：g/m3）星期一25.435.7星期二24.634.5星期三23.535.2星期四24.433.6星期五25.836.1星期六19.730.9星期日20.329.4（）在如
33、图所示的坐标系中作出表中数据的散点图；（）根据表中统计数据，求出线性回归方程x+（计算b时精确到0.01，计算a时精确到0.01）；（）为净化空气，该地决定下周起在工作日（星期一至星期五）限号假设限号时每个工作日的车流量为表中对应工作日的，试预测下周星期三的PM10浓度（精确到0.1）参考公式：，参考数据23.4，33.6，（xi）（yi）34.5，x35.5【分析】（）由已知表格中的数据直接作出散点图；（）分别求出的值，可得线性回归方程；（）求出下周星期三的车流量，代入线性回归方程得答案【解答】解：（）（）y关于x的线性回归方程为；（）下周星期三的车流量预计为（万辆）预测下周星期三的PM10
34、浓度为（g/m3）【点评】本题考查线性回归方程的求法，考查学生读取图表的能力和计算能力，是中档题22（12分）设p0，动圆C经过点M（p，0），且被y轴截得的弦长为2p，记动圆圆心C的轨迹为E（）求轨迹E的方程；（）求证：在轨迹E上存在点A，B，使得OAB（O为坐标原点）是以A为直角顶点的等腰直角三角形【分析】（）设动圆圆心C（x，y），半径为r，则r2（xp）2+y2，由圆C被y轴截得的弦长为2p，得r2p2+x2，由此能求出轨迹E的方程（）设A（，y0），（y00），则OA的斜率kOA，AB的斜率kAB，直线AB的方程为yy0（x），联立直线AB与抛物线E的方程，得，从而|AB|2（1+）
35、（2y0+）2，由|OA|2（）2+y02，记ty02，y00，a4p2，p0，则t0，a0，记f（t）|AB|2|OA|2a（2t+a）2t2，t0，记g（t）a（2ta）2t3，t0，则g（a）8a30，g（5a）4a30，根据零点存在定理，能证明在轨迹E上存在点A，B，使得OAB（O为坐标原点）是以A为直角顶点的等腰直角三角形【解答】解：（）设动圆圆心C（x，y），半径为r，圆C 过点M（p，0），r2（xp）2+y2，圆C被y轴截得的弦长为2p，r2p2+x2，由，得（xp）2+y2x2+p2，化简，得y22px，p0，轨迹E的方程为y22px，（p0）证明：（）设A（，y0），（y0
36、0），则OA的斜率kOA，OAAB，AB的斜率kAB，直线AB的方程为yy0（x），联立直线AB与抛物线E的方程，得：，解得，|AB|21+（）2（y0yB）2（1+）（2y0+）2，|OA|2（）2+y02，记ty02，y00，a4p2，p0，则t0，a0，记f（t）|AB|2|OA|2a（2t+a）2t2，t0，由题意0，记g（t）a（2ta）2t3，t0，g（a）8a30，g（5a）4a30，根据零点存在定理，存在t0（a，5a），使得g（t0）0，从而f（t0）0，当y0满足时，有|AB|OA|，此时OAB是以A为直角顶点的等腰直角三角形，在轨迹E上存在点A，B，使得OAB（O为坐标原点）是以A为直角顶点的等腰直角三角形【点评】本题考查动点的轨迹方程的求法，考查在轨迹E上存在点A，B，使得OAB（O为坐标原点）是以A为直角顶点的等腰直角三角形的证明，考查直线方程、抛物线等基础知识，考查运算求解能力，考查化归与转化思想，是难题
