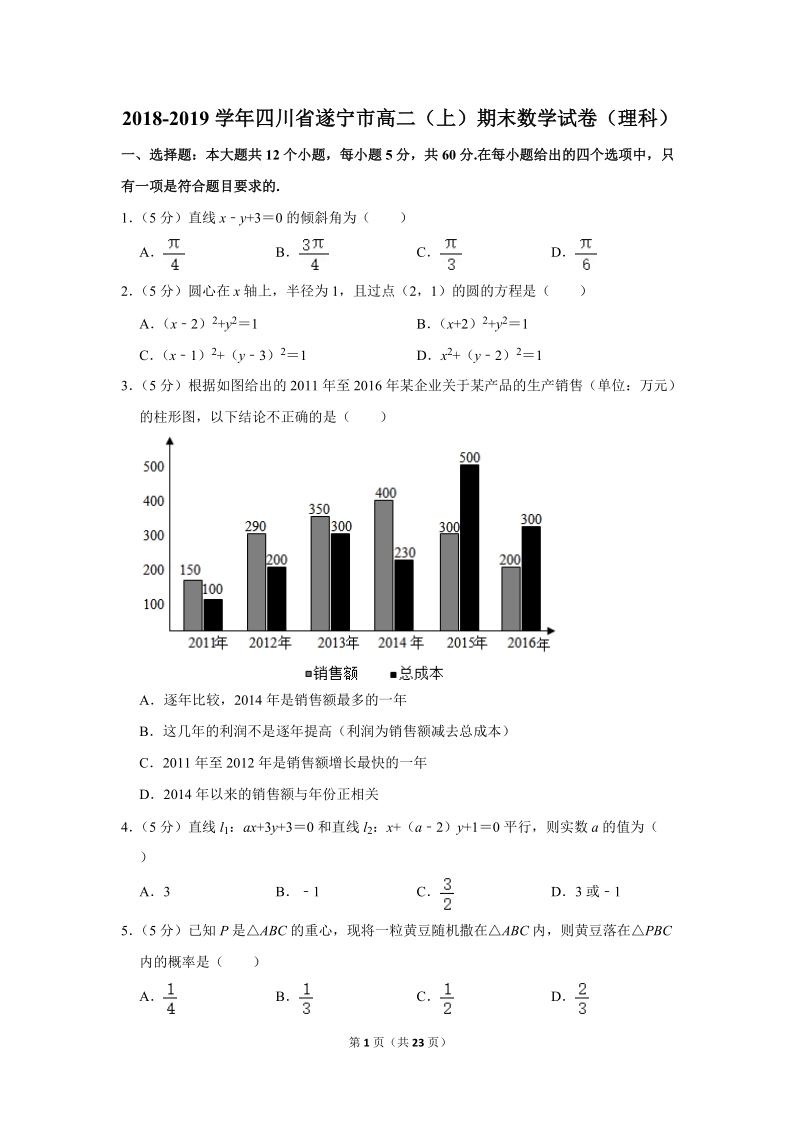
1、2018-2019学年四川省遂宁市高二（上）期末数学试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1（5分）直线xy+30的倾斜角为（）ABCD2（5分）圆心在x轴上，半径为1，且过点（2，1）的圆的方程是（）A（x2）2+y21B（x+2）2+y21C（x1）2+（y3）21Dx2+（y2）213（5分）根据如图给出的2011年至2016年某企业关于某产品的生产销售（单位：万元）的柱形图，以下结论不正确的是（）A逐年比较，2014年是销售额最多的一年B这几年的利润不是逐年提高（利润为销售额减去总成本）C2011年至201
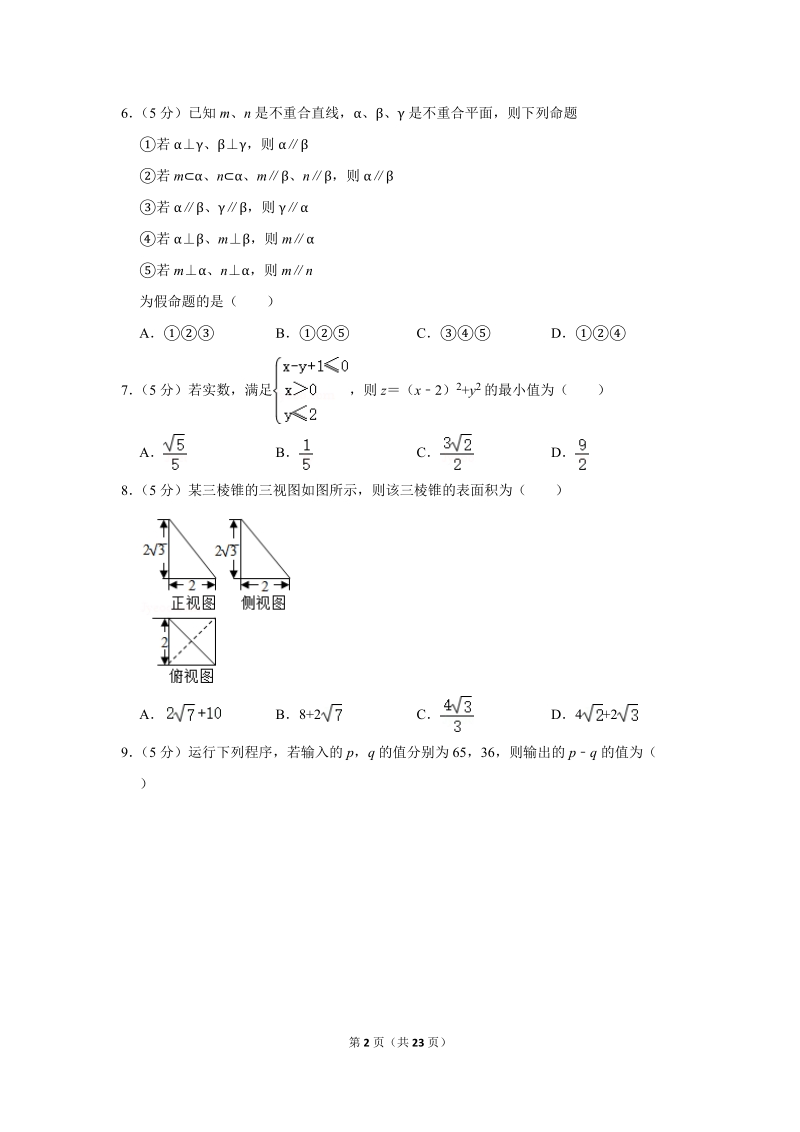
2、2年是销售额增长最快的一年D2014年以来的销售额与年份正相关4（5分）直线l1：ax+3y+30和直线l2：x+（a2）y+10平行，则实数a的值为（）A3B1CD3或15（5分）已知P是ABC的重心，现将一粒黄豆随机撒在ABC内，则黄豆落在PBC内的概率是（）ABCD6（5分）已知m、n是不重合直线，、是不重合平面，则下列命题若、，则若m、n、m、n，则若、，则若、m，则m若m、n，则mn为假命题的是（）ABCD7（5分）若实数，满足，则z（x2）2+y2的最小值为（）ABCD8（5分）某三棱锥的三视图如图所示，则该三棱锥的表面积为（）AB8+2CD4+29（5分）运行下列程序，若输入的p
3、，q的值分别为65，36，则输出的pq的值为（）A47B57C61D6710（5分）已知ABC的外接圆M经过点（0，1），（0，3），且圆心M在直线yx上若ABC的边长BC2，则sinBAC等于（）ABCD11（5分）已知三棱锥PABC中，PA，AB3，AC4，ABAC，PA面ABC，则此三棱锥的外接球的内接正方体的体积为（）A16B28C64D9612（5分）设点P是函数y图象上任意一点，点Q坐标为（2a，a3）（aR），当|PQ|取得最小值时圆C1：（xm）2+（y+a+1）24与圆C2：（x+n）2+（y+2）29相外切，则mn的最大值为（）A5BCD1二、填空题：本大题共4小题，每小题
4、5分，共20分13（5分）在空间直角坐标系中，点（1，2，3）关于yoz面对称的点的坐标为 14（5分）连续抛掷两枚骰子，向上的点数之和为6的概率为 15（5分）已知三棱锥ABCD中，ABCD，且直线AB与CD成60角，点M、N分别是BC、AD的中点，则直线AB和MN所成的角是 16（5分）在平面直角坐标系xOy中，点A（1，0），B（4，0），若在曲线C：x2+y22ax4ay+5a290上存在点P，使得|PB|2|PA|，则实数a的取值范围为 三、解答题：共70分解答应写出文字说明、证明过程或演算步骤17（10分）如图，在三棱锥PABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA
5、AC，PA6，BC8，DF5求证：（1）直线PA平面DEF；（2）平面BDE平面ABC18（12分）某城市理论预测2017年到2021年人口总数（单位：十万）与年份的关系如表所示：年份2017+x01234人口总数y5781119（1）请根据如表提供的数据，用最小二乘法求出y关于x的回归方程x+；（2）据此估计2022年该城市人口总数附：，参考数据：05+17+28+311+419132，02+12+22+32+423019（12分）已知直线2xy10与直线x2y+10交于点P（1）求过点P且平行于直线3x+4y150的直线l1的方程；（2）在（1）的条件下，若直线l1与圆x2+y22交于A、
6、B两点，求直线与圆截得的弦长|AB|20（12分）2012年“双节”期间，高速公路车辆较多某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/t）分成六段：（60，65），65，70），70，75），80，85），85，90）后得到如图的频率分布直方图（1）某调查公司在采样中，用到的是什么抽样方法？（2）求这40辆小型车辆车速的众数和中位数的估计值（3）若从车速在60，70）的车辆中任抽取2辆，求车速在65，70）的车辆至少有一辆的概率21（12分）如图，在四棱锥PABCD中，PA底面ABCD，
7、ABAD，ACCD，ABC60，PAABBC，E是PC的中点（1）证明：AE平面PCD；（2）求二面角APDC的正弦值22（12分）已知线段AB的端点B的坐标为（3，0），端点A在圆（x+3）2+y216上运动；（1）求线段AB中点M的轨迹方程；（2）过点C（1，1）的直线m与M的轨迹交于G、H两点，当GOH（O为坐标原点）的面积最大时，求直线m的方程并求出GOH面积的最大值（3）若点C（1，1），且P在M轨迹上运动，求的取值范围2018-2019学年四川省遂宁市高二（上）期末数学试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有
8、一项是符合题目要求的.1（5分）直线xy+30的倾斜角为（）ABCD【分析】由直线方程求出直线的斜率，再由斜率是倾斜角的正切值求解【解答】解：由直线xy+30，得其斜率为k1，设直线的倾斜角为（0），由tan1，得故选：A【点评】本题考查直线的倾斜角，考查直线倾斜角与斜率的关系，是基础题2（5分）圆心在x轴上，半径为1，且过点（2，1）的圆的方程是（）A（x2）2+y21B（x+2）2+y21C（x1）2+（y3）21Dx2+（y2）21【分析】设圆心为C（a，0），由题意可得1，求得a的值，可得要求的圆的方程【解答】解：圆心在x轴上，设圆心为C（a，0），再根据半径为1，且过点（2，1），可
9、得1，求得a2，故要求的圆的方程为 （x2）2+y21，故选：A【点评】本题主要考查求圆的标准方程的方法，求出圆心坐标的值，是解题的关键，属于基础题3（5分）根据如图给出的2011年至2016年某企业关于某产品的生产销售（单位：万元）的柱形图，以下结论不正确的是（）A逐年比较，2014年是销售额最多的一年B这几年的利润不是逐年提高（利润为销售额减去总成本）C2011年至2012年是销售额增长最快的一年D2014年以来的销售额与年份正相关【分析】从柱形图上看，2014年以来销售额与年份负相关【解答】解：在A中，由2011年至2016年某企业关于某产品的生产销售（单位：万元）的柱形图，逐年比较，2
10、014年是销售额最多的一年，故A正确；在B中，由2011年至2016年某企业关于某产品的生产销售（单位：万元）的柱形图，得这几年的利润不是逐年提高，故B正确；在C中，由2011年至2016年某企业关于某产品的生产销售（单位：万元）的柱形图，知2011年至2012年是销售额增长最快的一年，故C正确；在D中，从柱形图上看，2014年以来销售额与年份负相关，故D错误故选：D【点评】本题考查命题真假的判断，考查柱形图的识图读图等基础知识，考查数据处理能力、运算求解能力，考查函数与方程思想，是基础题4（5分）直线l1：ax+3y+30和直线l2：x+（a2）y+10平行，则实数a的值为（）A3B1CD3
11、或1【分析】利用直线与直线平行的性质直接求解【解答】解：直线l1：ax+3y+30和直线l2：x+（a2）y+10平行，解得a1实数a的值为1故选：B【点评】本题考查实数值的求法，考查直线与直线平行的性质等基础知识，考查运算求解能力，是基础题5（5分）已知P是ABC的重心，现将一粒黄豆随机撒在ABC内，则黄豆落在PBC内的概率是（）ABCD【分析】根据题意画出图形，结合图形求出对应图形的面积比即可【解答】解：如图所示，P是ABC的重心，现将一粒黄豆随机撒在ABC内，则黄豆落在PBC内的概率是：P故选：B【点评】本题考查了几何概型的概率计算问题，是基础题6（5分）已知m、n是不重合直线，、是不重
12、合平面，则下列命题若、，则若m、n、m、n，则若、，则若、m，则m若m、n，则mn为假命题的是（）ABCD【分析】由垂直于同一平面的两平面平行或相交，可判断；由面面平行的判定定理可判断；由平行平面的传递性可判断；由线面垂直和面面垂直的性质可判断；由垂直于同一平面的两直线平行可判断【解答】解：m、n是不重合直线，、是不重合平面，对于，若、，则或，相交，故错误；对于，若m、n、m、n，且m，n相交，则，故错误；对于，若、，则，故正确；对于，若、m，则m或m，故错误；对于，若m、n，则mn，故正确故选：D【点评】本题考查空间线线、线面和面面的位置关系的判断，考查平行和垂直的判断和性质，考查推理能力，
13、属于基础题7（5分）若实数，满足，则z（x2）2+y2的最小值为（）ABCD【分析】由约束条件作出可行域，再由z（x2）2+y2的几何意义，即可行域中点（x，y）与定点D（2，0）的距离的平方求解【解答】解：由题实数x，y满足可行域如图所示，z（x2）2+y2的几何意义表示可行域中点（x，y）与定点D（2，0）的距离的平方，由图可得，最小值为：DP，DP2（）2故选：D【点评】本题考查简单的线性规划，考查数形结合的解题思想方法，是中档题8（5分）某三棱锥的三视图如图所示，则该三棱锥的表面积为（）AB8+2CD4+2【分析】由三视图还原原几何体，可知该几何体为三棱锥PABC，底面三角形ABC为等
14、腰直角三角形，ABBC2，侧面三角形PAB与PBC全等，侧面三角形PAC为等腰三角形，PAPC然后由三角形面积公式求解【解答】解：由三视图还原原几何体如图，该几何体为三棱锥PABC，底面三角形ABC为等腰直角三角形，ABBC2，侧面三角形PAB与PBC全等，侧面三角形PAC为等腰三角形，PAPC则该三棱锥的表面积为S10+2故选：A【点评】本题考查由三视图求面积、体积，关键是由三视图还原原几何体，是中档题9（5分）运行下列程序，若输入的p，q的值分别为65，36，则输出的pq的值为（）A47B57C61D67【分析】根据题意，模拟程序框图的运行过程，得出该程序输出的结果是什么【解答】解：模拟程
15、序框图的运行过程，如下第一次运行，S101，p67，q31；第二次运行，S98，p69，q26；第三次运行，S95，p71，q21；第四次运行，S92，p73，q16，退出循环，此时pq57故选：B【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，从而得出正确的结论，是基础题10（5分）已知ABC的外接圆M经过点（0，1），（0，3），且圆心M在直线yx上若ABC的边长BC2，则sinBAC等于（）ABCD【分析】根据题意，设M的坐标为（x，y），半径为R，结合题意求出圆心的坐标，即可得R的值，结合正弦定理可得2R2，变形可得R的值，即可得答案【解答】解：根据题意，设M的坐
16、标为（x，y），半径为R，若圆M经过点（0，1），（0，3），则圆心在直线y2上，又由圆心在直线yx上，则x2，则圆心的坐标为（2，2），R，若ABC的边长BC2，则有2R2，变形可得：sinBAC；故选：A【点评】本题考查圆的标准方程以及正弦定理的应用，关键是求出圆的方程，属于基础题11（5分）已知三棱锥PABC中，PA，AB3，AC4，ABAC，PA面ABC，则此三棱锥的外接球的内接正方体的体积为（）A16B28C64D96【分析】以AB，AC，AP为棱构造长方体，则长方体的外接球就是三棱锥PABC的外接球，三棱锥PABC的外接球的半径R2，设此三棱锥的外接球的内接正方体的半径为a，则R2
17、，解得a4，由此能求出此三棱锥的外接球的内接正方体的体积【解答】解：三棱锥PABC中，PA，AB3，AC4，ABAC，PA面ABC，以AB，AC，AP为棱构造长方体，则长方体的外接球就是三棱锥PABC的外接球，三棱锥PABC的外接球的半径R2，设此三棱锥的外接球的内接正方体的半径为a，则R2，解得a4，此三棱锥的外接球的内接正方体的体积Va34364故选：C【点评】本题考查三棱锥的外接球的内接正方体的体积的求法，考查三棱锥及外接球、球的内接正方体等基础知识，考查运算求解能力，是中档题12（5分）设点P是函数y图象上任意一点，点Q坐标为（2a，a3）（aR），当|PQ|取得最小值时圆C1：（xm
18、）2+（y+a+1）24与圆C2：（x+n）2+（y+2）29相外切，则mn的最大值为（）A5BCD1【分析】根据题意，分析函数y的解析式可得（x1）2+y24，（y0），分析可得其对应的曲线为圆心在C（1，0），半径为2的圆的下部分，由Q的坐标可得Q在直线x2y60上，据此分析可得当|PQ|取得最小值时，PQ与直线x2y60垂直，此时有2，解可得a的值，即可得圆C1的方程，结合两圆外切的性质可得3+25，变形可得（m+n）225，由基本不等式的性质分析可得答案【解答】解：根据题意，函数y，即（x1）2+y24，（y0），对应的曲线为圆心在C（1，0），半径为2的圆的下部分，又由点Q（2a，a
19、3），则Q在直线x2y60上，当|PQ|取得最小值时，PQ与直线x2y60垂直，此时有2，解可得a1，圆C1：（xm）2+（y+2）24与圆C2：（x+n）2+（y+2）29相外切，则有3+25，变形可得：（m+n）225，则mn，故选：C【点评】本题考查圆的方程的综合应用，涉及直线和圆的位置关系的应用，根据函数的表达式确定对应曲线是解决本题的关键二、填空题：本大题共4小题，每小题5分，共20分13（5分）在空间直角坐标系中，点（1，2，3）关于yoz面对称的点的坐标为（1，2，3）【分析】根据点（x，y，z）关于yoz面对称的点的坐标为（x，y，z）【解答】解：点（1，2，3）关于yoz面对
20、称的点的坐标为（1，2，3）故答案为：（1，2，3）【点评】本题考查了点关于yoz面对称的点的坐标性质，考查了推理能力与计算能力，属于基础题14（5分）连续抛掷两枚骰子，向上的点数之和为6的概率为【分析】基本事件总数n6636，再用列举法求出向上的点数之和为6包含的基本事件有5个，由此能求出向上的点数之和为6的概率【解答】解：连续抛掷两枚骰子，基本事件总数n6636，向上的点数之和为6包含的基本事件有5个，分别为：（1，5），（5，1），（2，4），（4，2），（3，3），向上的点数之和为6的概率为p故答案为：【点评】本题考查概率的求法，考查列举法等基础知识，考查运算求解能力，是基础题15（5
21、分）已知三棱锥ABCD中，ABCD，且直线AB与CD成60角，点M、N分别是BC、AD的中点，则直线AB和MN所成的角是60或30【分析】取BD中点为O，连接MN、NO、MO根据题中条件可知：NOMO，由此能推导出AB和MN所成的角的大小【解答】解：取BD中点为O，连接MN、NO、MOABCD，OMCD，ONAB，直线AB与CD成60角，NOMO，MON60或MON120，当MON60时，MON是等边三角形，MNO60；当MON120时，MON是等腰三角形，MNO30故答案为：60或30【点评】本题考查异面直线所成的角的求法，解题时要认真审题，注意等价转化思想的合理运用16（5分）在平面直角坐
22、标系xOy中，点A（1，0），B（4，0），若在曲线C：x2+y22ax4ay+5a290上存在点P，使得|PB|2|PA|，则实数a的取值范围为，【分析】根据题意，设P（x，y），分析可得若|PB|2|PA|，则有（x4）2+y24（x1）2+4y2，变形可得x2+y24，进而可得P的轨迹为以O为圆心，半径为2的圆；将曲线C的方程变形为（xa）2+（y2a）29，可得以（a，2a）为圆心，半径为3的圆；据此分析可得若曲线C上存在点P使得|PB|2|PA|，则圆C与圆x2+y24有公共点，由圆与圆的位置关系可得322+3，解可得a的取值范围，即可得答案【解答】解：根据题意，设P（x，y），若|
23、PB|2|PA|，即|PB|24|PA|2，则有（x4）2+y24（x1）2+4y2，变形可得：x2+y24，即P的轨迹为以O为圆心，半径为2的圆，曲线Cx22ax+y24ay+5a290，即（xa）2+（y2a）29，则曲线C是以（a，2a）为圆心，半径为3的圆；若曲线C上存在点P使得|PB|2|PA|，则圆C与圆x2+y24有公共点，则有322+3，即1|a|5，解可得：a或a，即a的取值范围为：，；故答案为：，【点评】本题考查圆的方程应用以及轨迹方程的计算，关键求出P的轨迹方程三、解答题：共70分解答应写出文字说明、证明过程或演算步骤17（10分）如图，在三棱锥PABC中，D，E，F分别
24、为棱PC，AC，AB的中点，已知PAAC，PA6，BC8，DF5求证：（1）直线PA平面DEF；（2）平面BDE平面ABC【分析】（1）由D、E为PC、AC的中点，得出DEPA，从而得出PA平面DEF；（2）要证平面BDE平面ABC，只需证DE平面ABC，即证DEEF，且DEAC即可【解答】证明：（1）D、E为PC、AC的中点，DEPA，又PA平面DEF，DE平面DEF，PA平面DEF；（2）D、E为PC、AC的中点，DEPA3；又E、F为AC、AB的中点，EFBC4；DE2+EF2DF2，DEF90，DEEF；DEPA，PAAC，DEAC；ACEFE，DE平面ABC；DE平面BDE，平面BD
25、E平面ABC【点评】本题考查了空间中的平行与垂直问题，解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系，是基础题目18（12分）某城市理论预测2017年到2021年人口总数（单位：十万）与年份的关系如表所示：年份2017+x01234人口总数y5781119（1）请根据如表提供的数据，用最小二乘法求出y关于x的回归方程x+；（2）据此估计2022年该城市人口总数附：，参考数据：05+17+28+311+419132，02+12+22+32+4230【分析】（1）由表中数据结合已知求得，的值，则线性回归方程可求；（2）把x5代入线性回归方程求得y值，则答案可求【解答】解：（1）
26、由题中数表，知，（2分），（4分），（6分），（7分）回归方程为；（8分）（2）当x5时，（十万）196（万）（12分）【点评】本题考查线性回归方程的求法，考查计算能力，是基础题19（12分）已知直线2xy10与直线x2y+10交于点P（1）求过点P且平行于直线3x+4y150的直线l1的方程；（2）在（1）的条件下，若直线l1与圆x2+y22交于A、B两点，求直线与圆截得的弦长|AB|【分析】（1）根据题意，设直线l1的方程为3x+4y+m0，联立两个直线的方程，解可得P的坐标，将P的坐标代入直线方程，解可得m的值，即可得直线l1的方程，（2）根据题意，分析圆心的坐标和半径，求出圆心到直线的
27、距离，由直线与圆的位置关系可得答案【解答】解：（1）根据题意，设直线l1的方程为3x+4y+m0，直线2xy10与直线x2y+10交于点P，则，解可得，则P的坐标为（1，1）；点P在l1上，则有3+4m0，解可得m7；故直线l1的方程为3x+4y70；（2）圆x2+y22的圆心为（0，0），半径r，则圆心O（0，0）到直线l1：3x+4y70的距离，所以【点评】本题考查直线与圆的位置关系以及直线平行的判断，属于综合题20（12分）2012年“双节”期间，高速公路车辆较多某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在
28、某段高速公路的车速（km/t）分成六段：（60，65），65，70），70，75），80，85），85，90）后得到如图的频率分布直方图（1）某调查公司在采样中，用到的是什么抽样方法？（2）求这40辆小型车辆车速的众数和中位数的估计值（3）若从车速在60，70）的车辆中任抽取2辆，求车速在65，70）的车辆至少有一辆的概率【分析】（1）这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，是一个具有相同间隔的抽样，并且总体的个数比较多，这是一个系统抽样；（2）选出直方图中最高的矩形求出其底边的中点即为众数；求出从左边开始小矩形的面积和为0.5对应的横轴的左边即
29、为中位数；利用各个小矩形的面积乘以对应矩形的底边的中点的和为数据的平均数（3）从图中可知，车速在60，65）的车辆数和车速在65，70）的车辆数从车速在（60，70）的车辆中任抽取2辆，设车速在60，65）的车辆设为a，b，车速在65，70）的车辆设为c，d，e，f，列出各自的基本事件数，从而求出相应的概率即可【解答】解：（1）由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，是一个具有相同间隔的抽样，并且总体的个数比较多，这是一个系统抽样故调查公司在采样中，用到的是系统抽样，（2分）（2）众数的估计值为最高的矩形的中点，即众数的估计值等于77.5
30、 （4分）设图中虚线所对应的车速为x，则中位数的估计值为：0.015+0.025+0.045+0.06（x75）0.5，解得x77.5，即中位数的估计值为77.5 （6分）（3）从图中可知，车速在60，65）的车辆数为：m10.015402（辆），（7分）车速在65，70）的车辆数为：m20.025404（辆） （8分）设车速在60，65）的车辆设为a，b，车速在65，70）的车辆设为c，d，e，f，则所有基本事件有：（a，b），（a，c），（a，d），（a，e），（a，f），（b，c），（b，d），（b，e），（b，f），（c，d），（c，e），（c，f），（d，e），（d，f），（e，f）
31、共15种 （10分） 其中车速在65，70）的车辆至少有一辆的事件有：（a，c），（a，d），（a，e），（a，f），（b，c），（b，d），（b，e），（b，f），（c，d），（c，e），（c，f），（d，e），（d，f），（e，f）共14种 （12分）所以，车速在65，70）的车辆至少有一辆的概率为（13分）【点评】解决频率分布直方图的有关特征数问题，利用众数是最高矩形的底边中点；中位数是左右两边的矩形的面积相等的底边的值；平均数等于各个小矩形的面积乘以对应的矩形的底边中点的和此题把统计和概率结合在一起，比较新颖，也是高考的方向，应引起重视21（12分）如图，在四棱锥PABCD中，PA底面
32、ABCD，ABAD，ACCD，ABC60，PAABBC，E是PC的中点（1）证明：AE平面PCD；（2）求二面角APDC的正弦值【分析】（1）由PA底面ABCD，可得 CDPA，又CDAC，故CD面PAC，从而证得CDAE证明AEPD，再由 ABPD 可得 PD面ABE（2）过点A作AFPD，由（1）知，AE面PCD，故AFE是二面角APDC的一个平面角，用面积法求得AE 和AF，由 sinAFE求得结果【解答】（1）证明：在四棱锥PABCD中，因PA底面ABCD，CD平面ABCD，故CDPA由条件CDAC，PAACA，CD平面PAC又AE平面PAC，AECD由PAABBC，ABC60，可得A
33、CPAE是PC的中点，AEPC又PCCDC，综上得AE平面PCD（2）解：过点A作AFPD，垂足为F，连接EF由（1）知，AE面PCD，故AFE是二面角APDC的一个平面角设ACa，则AEa，从而AFaADa，PDa，从而AFa，故 sinAFE【点评】本题考查证明线线垂直、线面垂直的方法，找出二面角APDC的平面角是解题的难点，属于中档题22（12分）已知线段AB的端点B的坐标为（3，0），端点A在圆（x+3）2+y216上运动；（1）求线段AB中点M的轨迹方程；（2）过点C（1，1）的直线m与M的轨迹交于G、H两点，当GOH（O为坐标原点）的面积最大时，求直线m的方程并求出GOH面积的最大
34、值（3）若点C（1，1），且P在M轨迹上运动，求的取值范围【分析】（1）设点A（x0，y0），M（x，y）由中点坐标公式x02x3，y02y，代入圆的方程即可求出，（2）令GOH，则SGOHr2sin2sin，GOH时SABC面积最大为2，令lm：yxk（x1），即可求出直线的斜率，即可求出直线方程，（3）设点P（x，y），由于点B（3，0），C（1，1），则，令z2x+y+6，当直线与圆相切时，z取得最大或最小，即可求出【解答】解：（1）：设点A（x0，y0），M（x，y），由中点坐标公式有x，y，则x02x3，y02y，又点A（x0，y0）在圆（x+3）2+y216上，将A点坐标代入圆方程
35、得：M点的轨迹方程为：x2+y24；（2）令GOH，则SGOHr2sin2sin，当sin1，即GOH时SABC面积最大为2，又直线m过点（1，1），GOH，O到直线m的距离为，当直线m斜率不存在时Lm：x1，O到m的距离为1不满足，令lm：yxk（x1），则d，解得k1，故直线m的方程为：yx+2，（3）设点P（x，y），由于点B（3，0），C（1，1），则，令z2x+y+6，有y2x+z6，由于点P（x，y）在圆x2+y24上运动，故满足圆的方程当直线y2x+z6与圆相切时，z取得最大或最小，故有2，解得z62或z6+2，所以【点评】本题考查了点的轨迹方程，直线和圆的位置关系，考查了运算求解能力，属于中档题声明：
