1、中考总复习：勾股定理及其逆定理(提高) 巩固练习【巩固练习】一、选择题1（2011湖北黄石）将一个有45度角的三角板的直角顶点C放在一张宽为3cm的纸带边沿上，另一个顶点A在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30度角，如图，则三角板的最大边的长为（ ）.A. 3cm B. 6cm C. 3cm D. 6cm2在中，若，则是（ ）. 锐角三角形 . 钝角三角形 . 等腰三角形 . 直角三角形3. 如图，已知直角梯形ABCD中，ADBC，ABBC，AD=2，BC=DC=5，点P在BC上移动，则当PA+PD取最小值时，APD中边AP上的高为（ ）.A. B. C.D.34.如
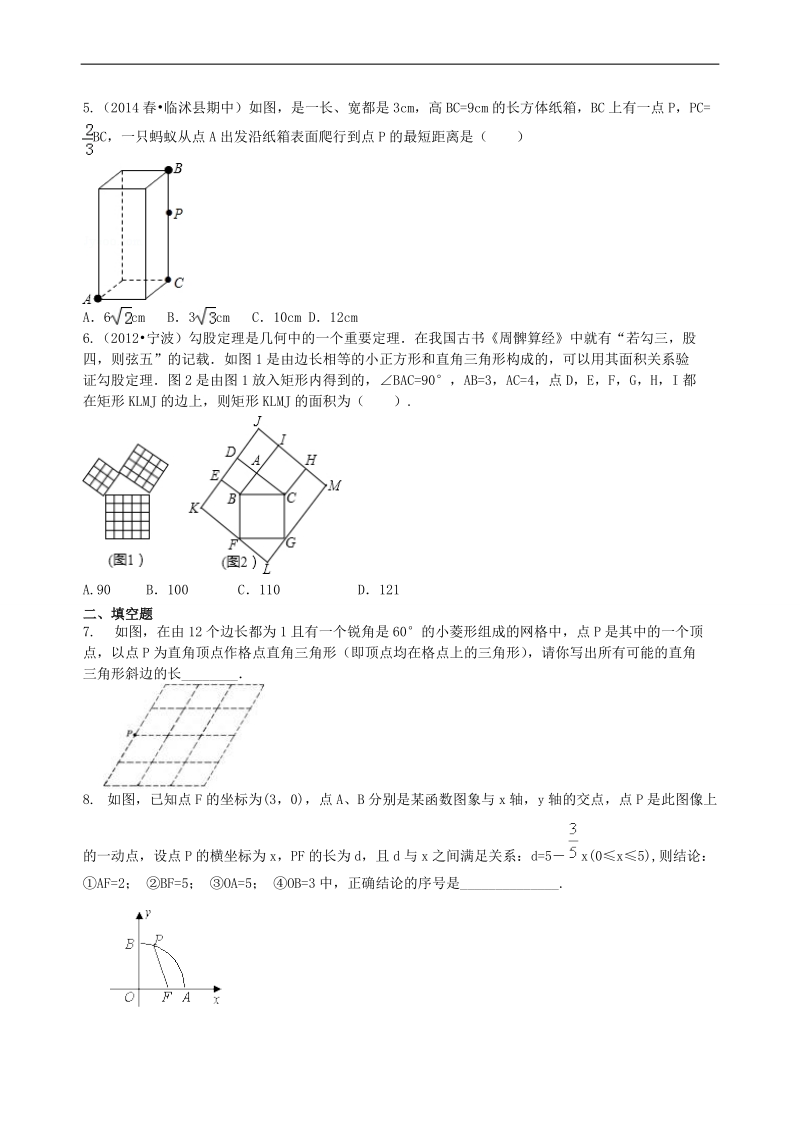
2、图，分别以直角的三边为直径向外作半圆设直线左边阴影部分的面积为，右边阴影部分的面积和为，则（ ）. A B C D无法确定5.（2014春临沭县期中）如图，是一长、宽都是3cm，高BC=9cm的长方体纸箱，BC上有一点P，PC=BC，一只蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是（）A6cmB3cmC10cmD12cm6.（2012宁波）勾股定理是几何中的一个重要定理在我国古书周髀算经中就有“若勾三，股四，则弦五”的记载如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理图2是由图1放入矩形内得到的，BAC=90，AB=3，AC=4，点D，E，F，G，H，I都在矩形
3、KLMJ的边上，则矩形KLMJ的面积为（）.A.90 B100 C110 D121 二、填空题7. 如图，在由12个边长都为1且有一个锐角是60的小菱形组成的网格中，点P是其中的一个顶点，以点P为直角顶点作格点直角三角形（即顶点均在格点上的三角形），请你写出所有可能的直角三角形斜边的长_ 8. 如图，已知点F的坐标为(3，0)，点A、B分别是某函数图象与x轴，y轴的交点，点P是此图像上的一动点，设点P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5x(0x5),则结论：AF=2； BF=5； OA=5； OB=3中，正确结论的序号是_. 9.（2014达州）如图，折叠矩形纸片ABCD，
4、使点B落在边AD上，折痕EF的两端分别在AB、BC上（含端点），且AB=6cm，BC=10cm则折痕EF的最大值是 cm10.勾股定理有着悠久的历史，它曾引起很多人的兴趣1955年希腊发行了二枚以勾股图为背景的邮票所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理在右图的勾股图中，已知ACB=90，BAC=30，AB=4作PQR使得R=90，点H在边QR上，点D，E在边PR上，点G，F在边PQ上，那么PQR的周长等于_.11观察下列一组数：列举：3、4、5，猜想：32=4+5；列举：5、12、13，猜想：52=12+13；列举：7、24、25，猜想：72=24+25；列举
5、：13、b、c，猜想：132=b+c；请你分析上述数据的规律，结合相关知识求得b=_,c=_.12.如图，正方体的棱长为2，O为AD的中点，则O，A1，B三点为顶点的三角形面积为_三、解答题13. 作长为、的线段.14.如图A、B为两个村庄，AB、BC、CD为公路，BD为田地，AD为河宽，且CD与AD互相垂直。现要从点E处开设通往村庄A、村庄B的一条电缆，现在共有两种铺设方案：方案一：EDAB；方案二：ECBA经测量得千米，BC=10千米，BDC=45，ABD=15已知：地下电缆的修建费为2万元千米，水下电缆的修建费为4万元千米求：1)河宽AD(结果保留根号)； 2)公路CD的长;3)哪种方案
6、铺设电缆的费用低?请说明理由。15. （2014春朝阳区期末）如图，RtABC中，ACB=90，BAC=30，AB=4，分别以AB、BC、AC为边作正方形ABED、BCFK、ACGH，再作RtPQR，使R=90，点H在边QR上，点D、E在边PR上，点G、F在边PQ上，求PQ的长？16刘卫同学在一次课外活动中，用硬纸片做了两个直角三角形，见图、图中，B=90，A=30，BC=6cm；图中，D=90，E=45，DE=4cm图是刘卫同学所做的一个实验：他将DEF的直角边DE与ABC的斜边AC重合在一起，并将DEF沿AC方向移动在移动过程中，D、E两点始终在AC边上（移动开始时点D与点A重合）（1）在
7、DEF沿AC方向移动的过程中，刘卫同学发现：F、C两点间的距离逐渐_.（填“不变”、“变大”或“变小”）（2）刘卫同学经过进一步地研究，编制了如下问题：问题：当DEF移动至什么位置，即AD的长为多少时，F、C的连线与AB平行？问题：当DEF移动至什么位置，即AD的长为多少时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形？问题：在DEF的移动过程中，是否存在某个位置，使得FCD=15？如果存在，求出AD的长度；如果不存在，请说明理由请你分别完成上述三个问题的解答过程 【答案与解析】一选择题1.【答案】D.【解析】过点A作AH垂直于纸带边沿于点H，在直角AHC中，AH=3，ACH=30
8、，AC=2AH=6, 再在等腰直角ABC中，AC=6, B=45，AB=. 故选D.2【答案】D.【解析】因为=4，所以，由勾股定理的逆定理可知：ABC是直角三角形, 答案选D.3【答案】C【解析】如图，过D点作DEBC于E,则DE=AB，AD=BE,EC=BCBE=3在RtCDE中，DE=,延长AB至F，使AB=BF，连接DF，交BC于P点，连接AP，这时候PA+PD取最小值，ADBC，B是AF中点，在RtABP中，AP=,故选C.4【答案】A.【解析】圆的面积为，设三条边长为a,b,c,分别表示三块阴影部分面积，用勾股定理即可.5【答案】A【解析】（1）如图1，AD=3cm，DP=3+6=
9、9cm，在RtADP中，AP=3cm；（2）如图2，AC=6cm，CP=3+3=6cm，RtADP中，AP=6cm综上，蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是6cm故选A6【答案】 C.二填空题7【答案】2，4，.【解析】如下图，可能的直角三角形斜边长有2，4，.8【答案】； ； .【解析】令x=0得到d=5,此时点P与点B重合，BF=5，由勾股定理的OB=4.令x=5得到d=2,此时点P与点A重合，可得AO=5，AF=2.9【答案】.【解析】如图，点F与点C重合时，折痕EF最大，由翻折的性质得，BC=BC=10cm，在RtBDC中，BD=8cm，AB=ADBD=108=2cm，设BE
10、=x，则BE=BE=x，AE=ABBE=6x，在RtABE中，AE2+AB2=BE2，即（6x）2+22=x2，解得x=，在RtBEF中，EF=cm故答案为：10【答案】27+13【解析】在直角ABC中，根据三角函数即可求得AC，进而由等边三角形的性质和正方形的性质及三角函数就可求得QR的长，在直角QRP中运用三角函数即可得到RP、QP的长，就可求出PQR的周长11.【答案】84,85.【解析】认真观察三个数之间的关系：首先发现每一组的三个数为勾股数，第一个数为从3开始连续的奇数，第二、三个数为连续的自然数；进一步发现第一个数的平方是第二、三个数的和；最后得出第n组数为（2n+1），（），（）
11、，由此规律解决问题12【答案】.【解析】直角AA1O和直角OBA中，利用勾股定理可以得到OA1=OB=，在直角A1AB中，利用勾股定理得A1B=2，过点O作高，交A1B与M，连接AM，则AOM是直角三角形，则AM=A1B=，OM=，OA1B的面积=A1BOM=三.综合题13【解析】作法：如图所示 （1）作直角边为1（单位长度）的等腰直角ACB，使AB为斜边；（2）作以AB为一条直角边，另一直角边为1的Rt。斜边为；（3）顺次这样做下去，最后做到直角三角形，这样斜边、的长 度就是、.14【解析】1).过B作BFAD交DA延长线于F，在RtABF中，可知BAF=60，AB， BF=6，在RtBFD
12、中，BDF=45， DF=BF=6， 2).过B作BGCD于G，则BG=6，BC=10，有CG=8， DC=CG+DG=14.3).设CE=x，则方案一、二费用分别为：，由可解得 当CE14时，方案一较省；当0CE时，方案二较省；当CE=时，方案一、二均可15【解析】解：延长BA交QR于点M，连接AR，AP在ABC和GFC中，ABCGFC（SAS），CGF=BAC=30，HGQ=60，HAC=BAD=90，BAC+DAH=180，又ADQR，RHA+DAH=180，RHA=BAC=30，QHG=60，Q=QHG=QGH=60，QHG是等边三角形AC=ABcos30=4=2，则QH=HA=HG=
13、AC=2，在直角HMA中，HM=AHsin60=2=3，AM=HAcos60=，在直角AMR中，MR=AD=AB=4QR=2+3+4=7+2，QP=2QR=14+4故答案为：14+416. 【解析】（1）变小；（2）问题：B=90，A=30，BC=6cmAC=12FDE=90，DEF=45，DE=4DF=4cm连接FC，设FCABFCD=A=30在RtFDC中，DC=4AD=AC-DC=12-4AD=12-4时，FCAB；问题：设AD=x，在RtFDC中，FC2=DC2+FD2=（12-x）2+16AC=12cm，DE=4cm，AD8cm，（I）当FC为斜边时，由AD2+BC2=FC2得，x2
14、+62=（12-x）2+16，x=；（II）当AD为斜边时，由FC2+BC2=AD2得，（12-x）2+16+62=x2，x=8（不合题意舍去）；（III）当BC为斜边时，由AD2+FC2=BC2得，x2+（12-x）2+16=36，x2-24x+160=0，方程无解，由（I）、（II）、（III）得，当x=时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形；另解：BC不能为斜边，FCCD，FC+AD12FC、AD中至少有一条线段的长度大于6，BC不能为斜边，由（I）、（II）、（III）得，当x=cm时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形；问题：解法一：不存在
15、这样的位置，使得FCD=15,理由如下：假设FCD=15EFC=30作EFC的平分线，交AC于点P则EFP=CFP=15，DFE+EFP=60PD=4，PC=PF=2FD=8PC+PD=8+412不存在这样的位置，使得FCD=15;解法二：不存在这样的位置，使得FCD=15假设FCE=15AD=x由FED=45得EFC=30作EHFC，垂足为HHE=EF=2CE=AC-AD-DE=8-x且FC2=（12-x）2+16FDC=EHC=90DCF为公共角CHECDF=又（）2=（）2=（）2=，即=整理后，得到方程x2-8x-32=0x1=4-40（不符合题意，舍去）x2=4+48（不符合题意，舍去）不存在这样的位置，使得FCD=15
