1、5.1平面向量的概念及线性运算最新考纲考情考向分析1.了解向量的实际背景2.理解平面向量的概念，理解两个向量相等的含义3.理解向量的几何表示4.掌握向量加法、减法的运算，并理解其几何意义5.掌握向量数乘的运算及其几何意义，理解两个向量共线的含义6.了解向量线性运算的性质及其几何意义.主要考查平面向量的线性运算(加法、减法、数乘向量)及其几何意义、共线向量定理，常与三角函数、解析几何交汇考查，有时也会有创新的新定义问题；题型以选择题、填空题为主，属于中低档题目偶尔会在解答题中作为工具出现.1向量的有关概念名称定义备注向量具有大小和方向的量；向量的大小叫做向量的长度(或称模)平面向量是自由向量零向
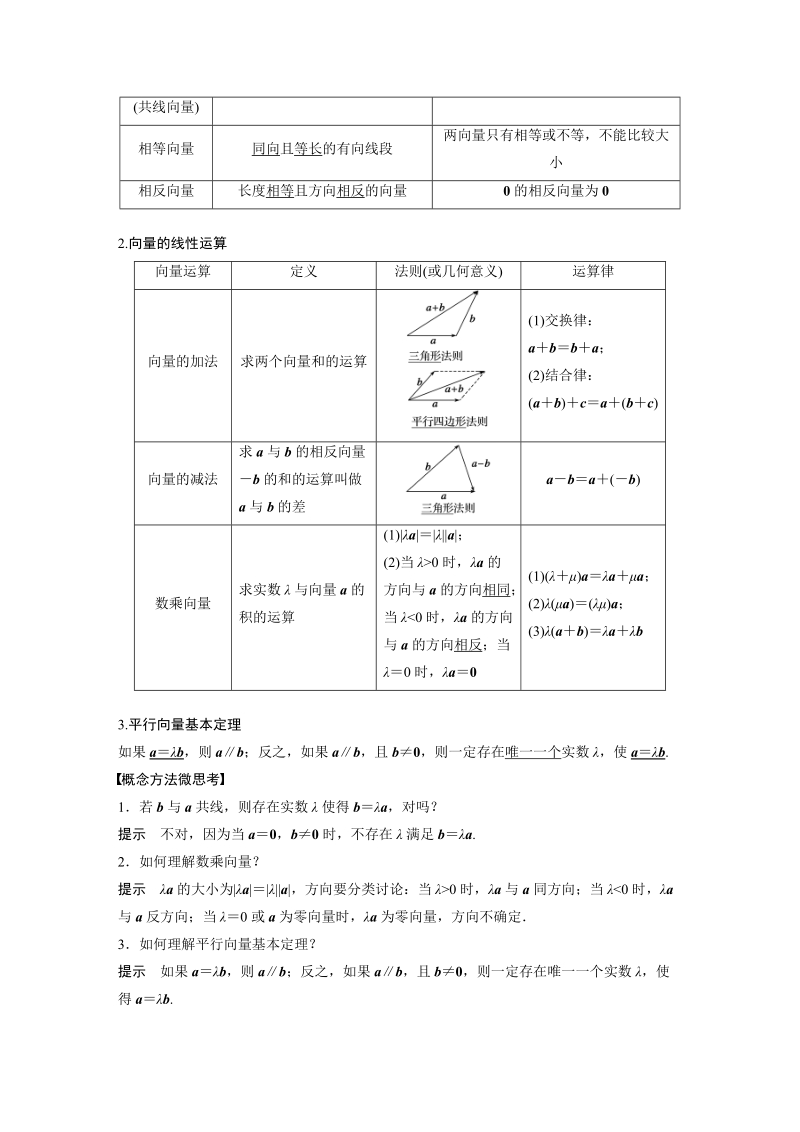
2、量长度为0的向量；其方向不确定记作0单位向量长度等于1个单位的向量非零向量a的单位向量为平行向量(共线向量)共线向量的方向相同或相反0与任一向量平行或共线相等向量同向且等长的有向线段两向量只有相等或不等，不能比较大小相反向量长度相等且方向相反的向量0的相反向量为02.向量的线性运算向量运算定义法则(或几何意义)运算律向量的加法求两个向量和的运算(1)交换律：abba；(2)结合律：(ab)ca(bc)向量的减法求a与b的相反向量b的和的运算叫做a与b的差aba(b)数乘向量求实数与向量a的积的运算(1)|a|a|；(2)当0时，a的方向与a的方向相同；当0时，a与a同方向；当|b|答案A解析方
3、法一|ab|ab|，|ab|2|ab|2.a2b22aba2b22ab.ab0.ab.故选A.方法二利用向量加法的平行四边形法则在ABCD中，设a，b，由|ab|ab|知，|，从而四边形ABCD为矩形，即ABAD，故ab.故选A.命题点2向量的线性运算例2 (1)(2019包头模拟)在平行四边形ABCD中，点E为CD的中点，BE与AC的交点为F，设a，b，则向量等于()A.ab BabCab D.ab答案C解析()ab，故选C.(2)(2018全国)在ABC中，AD为BC边上的中线，E为AD的中点，则等于()A. B.C. D.答案A解析作出示意图如图所示()().故选A.命题点3根据向量线性
4、运算求参数例3 在锐角ABC中，3，xy，则_.答案3解析由题意得3()，即43，亦即，则x，y.故3.思维升华 平面向量线性运算问题的常见类型及解题策略(1)向量加法或减法的几何意义向量加法和减法均适合三角形法则(2)求已知向量的和共起点的向量求和用平行四边形法则；求差用三角形法则；求首尾相连向量的和用三角形法则(3)求参数问题可以通过研究向量间的关系，通过向量的运算将向量表示出来，进行比较，求参数的值跟踪训练1 (1)在ABC中，点D，E分别在边BC，AC上，且2，3，若a，b，则等于()A.ab B.abCab Dab答案C解析()ab，故选C.(2)(2018营口模拟)在平行四边形AB
5、CD中，E，F分别为边BC，CD的中点，若xy(x，yR)，则xy_.答案2解析由题意得，因为xy，所以，所以解得所以xy2.题型三平行向量基本定理的应用例4 设两个非零向量a与b不共线(1)若ab，2a8b，3(ab)，求证：A，B，D三点共线；(2)试确定实数k，使kab和akb共线(1)证明ab，2a8b，3(ab)，2a8b3(ab)2a8b3a3b5(ab)5，共线又它们有公共点B，A，B，D三点共线(2)解假设kab与akb共线，则存在实数，使kab(akb)，即(k)a(k1)b.又a，b是两个不共线的非零向量，kk10.消去，得k210，k1.引申探究1若将本例(1)中“2a8
6、b”改为“amb”，则m为何值时，A，B，D三点共线？解(amb)3(ab)4a(m3)b，即4a(m3)b.若A，B，D三点共线，则存在实数，使.即4a(m3)b(ab)所以解得m7.故当m7时，A，B，D三点共线2若将本例(2)中的“共线”改为“反向共线”，则k为何值？解因为kab与akb反向共线，所以存在实数，使kab(akb)(0)所以所以k1.又1，因为，所以m，即，又知A，B，D三点共线，所以1，即m，所以1，故选B.15已知A，B，C是平面上不共线的三点，O是ABC的重心，动点P满足，则点P一定为ABC的()ABC边中线的中点BBC边中线的三等分点(非重心)C重心DBC边的中点答
7、案B解析设BC的中点为M，则，(2)，即32，也就是2，P，M，A三点共线，且P是AM上靠近A点的一个三等分点16设W是由一平面内的n(n3)个向量组成的集合若aW，且a的模不小于W中除a外的所有向量和的模则称a是W的极大向量有下列命题：若W中每个向量的方向都相同，则W中必存在一个极大向量；给定平面内两个不共线向量a，b，在该平面内总存在唯一的平面向量cab，使得Wa，b，c中的每个元素都是极大向量；若W1a1，a2，a3，W2b1，b2，b3中的每个元素都是极大向量，且W1，W2中无公共元素，则W1W2中的每一个元素也都是极大向量其中真命题的序号是_答案解析若有几个方向相同，模相等的向量，则无极大向量，故不正确；由题意得a，b，c围成闭合三角形，则任意向量的模等于除它本身外所有向量和的模，故正确；3个向量都是极大向量，等价于3个向量之和为0，故W1a1，a2，a3，W2b1，b2，b3中的每个元素都是极大向量时，W1W2中的每一个元素也都是极大向量，故正确
