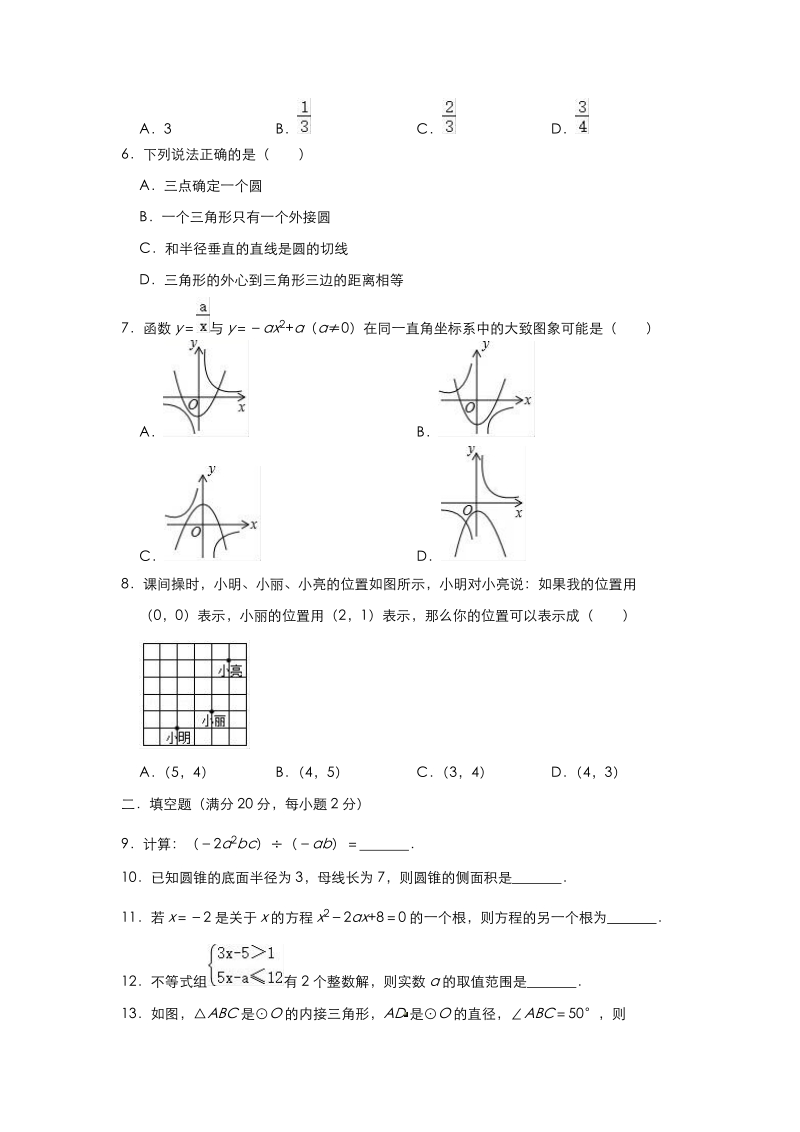
1、一选择题（满分16分，每小题2分）1平面直角坐标系内一点P（2，3）关于原点对称的点的坐标是（）A（3，2）B（2，3）C（2，3）D（2，3）2如图，ABC的顶点都在正方形网格的格点上，则cosBAC的值为（）ABCD3一组数据由m个a和n个b组成，那么这组数据的平均数是（）ABCD4函数y与yax2（a0）在同一平面直角坐标系中的图象可能是（）ABCD5如图，AD、BE是锐角三角形的两条高，SABC18，SDEC2，则cosC等于（）A3BCD6下列说法正确的是（）A三点确定一个圆B一个三角形只有一个外接圆C和半径垂直的直线是圆的切线D三角形的外心到三角形三边的距离相等7函数y与yax2+
2、a（a0）在同一直角坐标系中的大致图象可能是（）ABCD8课间操时，小明、小丽、小亮的位置如图所示，小明对小亮说：如果我的位置用（0，0）表示，小丽的位置用（2，1）表示，那么你的位置可以表示成（）A（5，4）B（4，5）C（3，4）D（4，3）二填空题（满分20分，每小题2分）9计算：（2a2bc）（ab） 10已知圆锥的底面半径为3，母线长为7，则圆锥的侧面积是 11若x2是关于x的方程x22ax+80的一个根，则方程的另一个根为 12不等式组有2个整数解，则实数a的取值范围是 13如图，ABC是O的内接三角形，AD是O的直径，ABC
3、50，则CAD 14如图，直线y2x+2与x轴y轴分别相交于点A、B，四边形ABCD是正方形，曲线y在第一象限经过点D则k 15二次函数yax2+bx+c的图象与x轴相交于（1，0）和（5，0）两点，则该抛物线的对称轴是 16在ABC中，B45，C75，AC2，则BC的值为 17如图，已知点A（x1，y1），B（x2，y2）在一次函数ykx+b（b0）的图象上，则y1 y2（填“”或“”）18如图，等边三角形ABC的边长为cm，在AC，BC边上各取一点E，F，使得AECF，连接AF，BE相交于点P（1）则APB
4、 度；（2）当点E从点A运动到点C时，则动点P经过的路径长为 cm三解答题（共9小题，满分11分）19计算：（1）|2|+2cos30（）2+（tan45）1（2）（）24sin60+（2）0+20（4分）解方程：（1）3x（x1）2x2（2）21如图，在ABCD中，AE平分BAD，交BC于点E，BF平分ABC，交AD于点F，AE与BF交于点O，连接EF求证：四边形ABEF是菱形22（7分）如图，活动课上，小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度，她先在山脚下的点E处测得山顶A的仰角是30，然后，她沿着坡度i1：1的斜坡按速度20米/分步行15分钟到达C处，此时
5、，测得点A的俯角是15图中点A、B、E、D、C在同一平面内，且点D、E、B在同一水平直线上，求出建筑地所在山坡AE的高度AB（精确到0.1米，参考数据：1.41）23某市计划在十二年内通过公租房建设，解决低收入人群的住房问题已知前7年，每年竣工投入使用的公租房面积y（单位：百万平方米），与时间x（第x年）的关系构成一次函数，（1x7且x为整数），且第一和第三年竣工投入使的公租房面积分别为和百万平方米；后5年每年竣工投入使用的公租房面积y（单位：百万平方米），与时间x（第x年）的关系是yx+（7x12且x为整数）（1）已知第6年竣工投入使用的公租房面积可解决20万人的住房问题，如果人均住房面积，
6、最后一年要比第6年提高20%，那么最后一年竣工投入使用的公租房面积可解决多少万人的住房问题？（2）受物价上涨等因素的影响，已知这12年中，每年竣工投入使用的公租房的租金各不相同，且第一年，一年38元/m2，第二年，一年40元/m2，第三年，一年42元/m2，第四年，一年44元/m2以此类推，分析说明每平方米的年租金和时间能否构成函数，如果能，直接写出函数解析式；（3）在（2）的条件下，假设每年的公租房当年全部出租完，写出这12年中每年竣工投入使用的公租房的年租金W关于时间x的函数解析式，并求出W的最大值（单位：亿元）如果在W取得最大值的这一年，老张租用了58m2的房子，计算老张这一年应交付的租
7、金24如图，ABC内接于O， AD与BC是O的直径，延长线段AC至点G，使AGAD，连接DG交O于点E，EFAB交AG于点F（1）求证：EF与O相切（2）若EF2，AC4，求扇形OAC的面积25如图，在直角坐标系中，长方形ABCD（每个内角都是90）的顶点的坐标分别是A（0，m），B（n，0），（mn0），点E在AD上，AEAB，点F在y轴上，OFOB，BF的延长线与DA的延长线交于点M，EF与AB交于点N（1）试求点E的坐标（用含m，n的式子表示）；（2）求证：AMAN；（3）若ABCD12cm，BC20cm，动点P从B出发，以2cm/s的速度沿BC向C运动的同时，动点Q从C出发，以vcm/
8、s的速度沿CD向D运动，是否存在这样的v值，使得ABP与PQC全等？若存在，请求出v值；若不存在，请说明理由26如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG2OD，OE2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE（1）求证：DEAG；（2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转角（0360）得到正方形OEFG，如图2在旋转过程中，当OAG是直角时，求的度数；若正方形ABCD的边长为1，在旋转过程中，求AF长的最大值和此时的度数，直接写出结果不必说明理由27如图1，在平面直角坐标系中，抛物线yax2+bx+3（a0）与x轴分别
9、交于A（3，0），B两点，与y轴交于点C，抛物线的顶点E（1，4），对称轴交x轴于点F（1）请直接写出这条抛物线和直线AE、直线AC的解析式；（2）连接AC、AE、CE，判断ACE的形状，并说明理由；（3）如图2，点D是抛物线上一动点，它的横坐标为m，且3m1，过点D作DKx轴于点K，DK分别交线段AE、AC于点G、H在点D的运动过程中，DG、GH、HK这三条线段能否相等？若相等，请求出点D的坐标；若不相等，请说明理由；在的条件下，判断CG与AE的数量关系，并直接写出结论参考答案一选择题1解：点P（2，3）关于原点对称的点的坐标是（2，3）故选：D2解：过B作BHAC交AC的延长线于H，AB5
10、，AH3，cosBAC，故选：C3解：该组数据的和ma+nb，该组数据的个数m+n；则平均数；故选：D4解：a0时，y的函数图象位于第一三象限，yax2的函数图象位于第一二象限且经过原点，a0时，y的函数图象位于第二四象限，yax2的函数图象位于第三四象限且经过原点，纵观各选项，只有D选项图形符合故选：D5解：AD、BE是锐角三角形的两条高，A、B、D、E四点共圆，BACCDE，又CC，ABCDEC，SABC18，SDEC2，3，在直角三角形ADC中，cosC故选：B6解：A、不在同一直线上的三点确定一个圆；故本选项错误；B、一个三角形只有一个外接圆；故本选项正确；C、经过半径的外端且垂直于这
11、条半径的直线是圆的切线；故本选项错误；D、三角形的外心到三角形三个顶点的距离相等；故本选项错误故选：B7解：A、反比例函数图象在第一、三象限，因此a0，二次函数开口向上，则a0，可得a0，抛物线与y轴交于负半轴，则a0，前后矛盾，故此选项错误；B、反比例函数图象在第二、四象限，因此a0，二次函数开口向上，则a0，可得a0，抛物线与y轴交于负半轴，则a0，前后统一，故此选项正确；C、反比例函数图象在第二、四象限，因此a0，二次函数开口向下，则a0，可得a0，抛物线与y轴交于正半轴，则a0前后矛盾，故此选项错误；D、反比例函数图象在第一、三象限，因此a0，二次函数开口向下，则a0，可得a0，抛物线
12、与y轴交于负半轴，则a0，前后矛盾，故此选项错误；故选：B8解：如果小明的位置用（0，0）表示，小丽的位置用（2，1）表示，如图所示就是以小明为原点的平面直角坐标系的第一象限，所以小亮的位置为（3，4）故选：C二填空题9解：原式2ac故答案为：2ac10解：圆锥的侧面积23721故答案为2111解：设方程的另一个根为x1，根据根与系数的关系有：2x18，解得x14故答案为：412解：解不等式3x51，得：x2，解不等式5xa12，得：x，不等式组有2个整数解，其整数解为3和4，则45，解得：8a13，故答案为：8a1313解：连接CD，AD是O的直径，ACD90，DABC50，CAD90D40
13、故答案为：4014解：作DEx轴，垂足为E，连ODDAE+BAO90，OBA+BAO90，DAEOBA，又BOAAED，ABDA，BOAAED（HL），OADEy2x+2，可知B（0，2），A（1，0），OADE1，OEOA+AE1+23，SDOEOEDE31，k23故答案为：315解：二次函数yax2+bx+c的图象与x轴相交于（1，0）和（5，0）两点，其对称轴为：x2故答案为：x216解：如图所示，过点C作CDAB，垂足为D在RtBCD中，B45，BCD45，BCA75，ACDACBBCD30在RtACD中，cosACDcos30，CDAC在RtACD中，sinBsin45CBDC故答案
14、为：17解：由函数的图象可知y随x的增大而减小，点A（x1，y1），B（x2，y2）在一次函数ykx+b（b0）的图象上，x1x2，y1y2，故答案为18解：（1）ABC为等边三角形，ABAC，CCAB60，在ABE和CAF中，ABECAF（SAS），AFBE，ABECAF，APEBPFABP+BAP，APEBAP+CAF60，APB180APE120；故答案为：120；（2）若AFBE，AECF时，点P的路径是一段弧，O为圆心，如图所示：当E为AC的中点时，点P经过弧AB的中点，此时ABP为等腰三角形，且ABPBAP30，AOB120，作OMAB于M，则AMBMAB，AOM60，又AB，OA
15、1，点P的路径是l；故答案为：三解答题19解：（1）原式0；（2）原式520解：（1）3x23x2x2，3x23x2x+20，3x25x+20，因式分解可得：（3x2）（x1）0，则3x20或x10，所以方程的解为；（2）两边乘以x（x2），得3（x2）2x，解得x6，检验：将x6代入x（x2）0，所以x6是原方程的解21证明：四边形ABCD是平行四边形，ADBC，AFBFBE，BF平分ABC，ABFFBE，ABFAFB，ABAF，同理ABBE，AFBE，ABBE，四边形ABEF是平行四边形，四边形ABEF是菱形22解：作EFAC于点F，根据题意，CE2015300米，i1：1，tanCED1
16、，CEDDCE45，ECF90451530，EFCE150米，CEF60，AEB30，AEF18045603045，AFEF150米，AE（米），AB150105.8（米）答：建筑地所在山坡AE的高度AB约为105.8米23解：（1）设ykx+b（1x7），由题意得，解得k，b4yx+4（1x7）x6时，y6+433002015，15（1+20%）18，又x12时，y12+1001812.5万人，所以最后一年可解决12.5万人的住房问题；（2）由于每平方米的年租金和时间都是变量，且对于每一个确定的时间x的值，每平方米的年租金m都有唯一的值与它对应，所以它们能构成函数由题意知m2x+36（1x1
17、2）（3）解：W当x3时Wmax147，x8时Wmax143，147143当x3时，年租金最大，Wmax1.47亿元当x3时，m23+3642元58422436元答：老张这一年应交租金为2436元24（1）证明：如图1，连接OE，ODOE，DOED，ADAG，DG，OEDG，OEAG，BC是O的直径，BAC90，EFAB，BAF+AFE180，AFE90，OEAG，OEF180AFE90，OEEF，EF与O相切；（2）解：如图2，连接OE，过点O作OHAC于点H，AC4，CH，OHFHFEOEF90，四边形OEFH是矩形，在RtOHC中，OC4，OAACOC4，AOC是等边三角形，AOC60，
18、S扇形OAC25解：（1）过E作EGAO于GEGAEABAOB90，EAG+AEG90，EAG+BAO90，BAOAEG，AEAB，EGAAOB（AAS），EGOAm，AGOBnE（m，m+n）（2）OBOF，BOF90，OFBOBF45，EGAAOB，AGOBOF，OAFGEG，GFE45，EFB90，NAENFB90，ANEFNB，AENABM，EANBAM90，EABA，EANBAM（ASA），ANAM（3）如图，ABP与PCQ全等，ABPPCQ90有两种情形：当ABCD，PBCP时，t5（s），v（cm/s），当ABPC，CQPB时，PB20128，t4（s），v2（cm/s）26解：
19、（1）如图1，延长ED交AG于点H，点O是正方形ABCD两对角线的交点，OAOD，OAOD，OGOE，在AOG和DOE中，AOGDOE，AGODEO，AGO+GAO90，GAO+DEO90，AHE90，即DEAG；（2）在旋转过程中，OAG成为直角有两种情况：（）由0增大到90过程中，当OAG90时，OAODOGOG，在RtOAG中，sinAGO，AGO30，OAOD，OAAG，ODAG，DOGAGO30，即30；（）由90增大到180过程中，当OAG90时，同理可求BOG30，18030150综上所述，当OAG90时，30或150如图3，当旋转到A、O、F在一条直线上时，AF的长最大，正方形
20、ABCD的边长为1，OAODOCOB，OG2OD，OGOG，OF2，AFAO+OF+2，COE45，此时31527解：（1）抛物线的表达式为：ya（x+1）2+4a（x2+2x+1）+4ax2+4ax+a+4，故a+43，解得：a1，故抛物线的表达式为：yx22x+3；将点A、E的坐标代入一次函数表达式并解得：直线AE的表达式为：y2x+6；同理可得：直线AC的表达式为：yx+3；（2）点A、C、E的坐标分别为：（3，0）、（0，3）、（1，4），则AC218，CE22，AE220，故AC2+CE2AE2，则ACE为直角三角形；（3）设点D、G、H的坐标分别为：（x，x22x+3）、（x，2x+6）、（x，x+3），DGx22x+32x6x24x3；HKx+3；GH2x+6x3x+3；当DGHK时，x24x3x+3，解得：x2或3（舍去3），故x2，当x2时，DGHKGH1，故DG、GH、HK这三条线段相等时，点D的坐标为：（2，3）；CG；AE2，故AE2CG
