1、提分专练(七)以圆为背景的综合计算与证明题|类型1|圆与切线有关的问题1.2018咸宁如图T7-1,以ABC的边AC为直径的O恰为ABC的外接圆,ABC的平分线交O于点D,过点D作DEAC交BC的延长线于点E.(1)求证:DE是O的切线;(2)若AB=25,BC=5,求DE的长.图T7-12.2019锦州如图T7-2,M,N是以AB为直径的O上的点,且AN=BN,弦MN交AB于点C,BM平分ABD,MFBD于点F.(1)求证:MF是O的切线;(2)若CN=3,BN=4,求CM的长.图T7-2|类型2|圆与四边形结合的问题3.2019福建如图T7-3,四边形ABCD内接于O,AB=AC,ACBD
2、,垂足为E,点F在BD的延长线上,且DF=DC,连接AF,CF.(1)求证:BAC=2CAD;(2)若AF=10,BC=45,求tanBAD的值.图T7-34.2018镇江如图T7-4,平行四边形ABCD中,ABAC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的P与对角线AC交于A,E两点.(1)如图,当P与边CD相切于点F时,求AP的长;(2)不难发现,当P与边CD相切时,P与平行四边形ABCD的边有三个公共点,随着AP的变化,P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的长的取值范围:.图T7-4|类型3|圆与三角函数结合
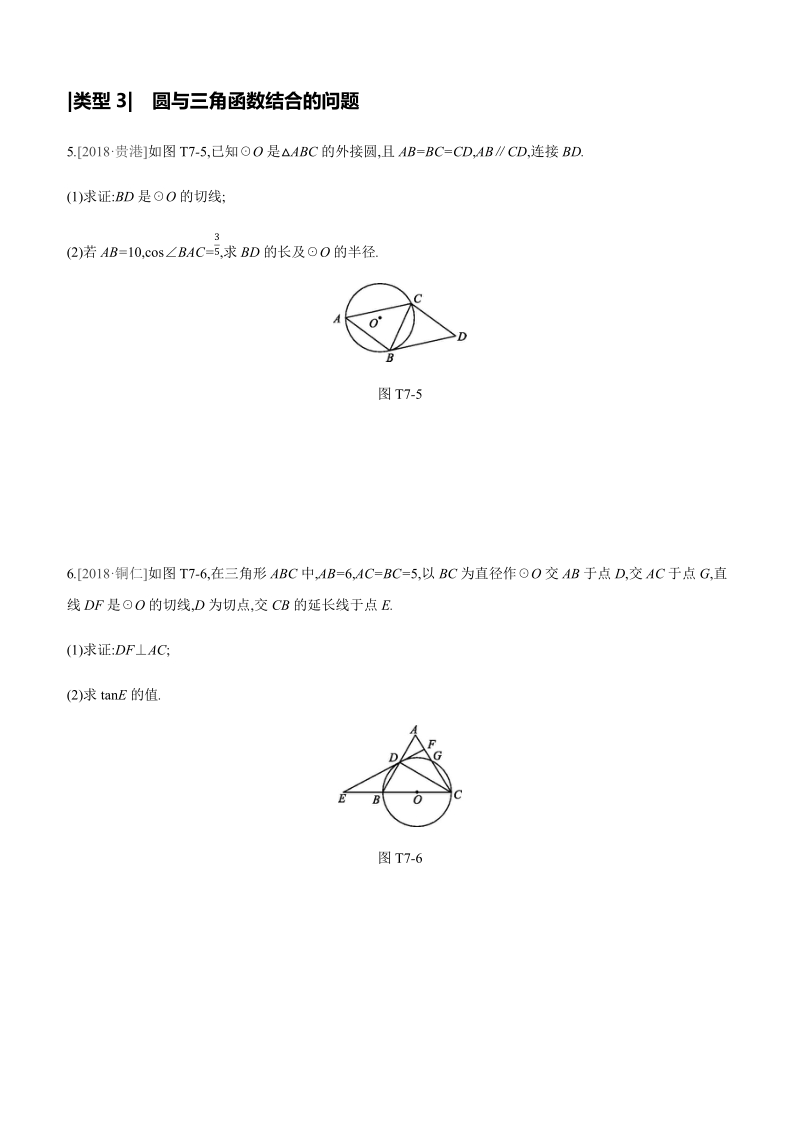
3、的问题5.2018贵港如图T7-5,已知O是ABC的外接圆,且AB=BC=CD,ABCD,连接BD.(1)求证:BD是O的切线;(2)若AB=10,cosBAC=35,求BD的长及O的半径.图T7-56.2018铜仁如图T7-6,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作O交AB于点D,交AC于点G,直线DF是O的切线,D为切点,交CB的延长线于点E.(1)求证:DFAC;(2)求tanE的值.图T7-6|类型4|圆与相似三角形结合的问题7.2019贵港如图T7-7,在矩形ABCD中,以BC边为直径作半圆O,OEOA交CD边于点E,对角线AC与半圆O的另一个交点为P,连接AE.
4、(1)求证:AE是半圆O的切线;(2)若PA=2,PC=4,求AE的长.图T7-78.2017苏州如图T7-8,已知ABC内接于O,AB是直径,点D在O上,ODBC,过点D作DEAB,垂足为E,连接CD交OE于点F.(1)求证:DOEABC;(2)求证:ODF=BDE;(3)连接OC,设DOE的面积为S1,四边形BCOD的面积为S2,若S1S2=27,求sinA的值.图T7-8【参考答案】1.解:(1)证明:连接OD,AC是O的直径,ABC=90,BD平分ABC,ABD=45,AOD=90.DEAC,ODE=AOD=90,DE是O的切线.(2)在RtABC中,AB=25,BC=5,AC=AB2
5、+BC2=5,OD=52.过点C作CGDE,垂足为G,则四边形ODGC为正方形,DG=CG=OD=52.DEAC,CEG=ACB,又ABC=CGE=90,ABCCGE,CGGE=ABBC,即52GE=255,解得GE=54,DE=DG+GE=154.2.解:(1)证明:连接OM,如图.OM=OB,OMB=OBM.BM平分ABD,OBM=MBF,OMB=MBF,OMBF,MFBD,OMMF,即OMF=90,MF是O的切线.(2)如图,连接AN,ON.AN=BN,AN=BN=4.AB是直径,AN=BN,ANB=90,ONAB,AB=AN2+BN2=42.AO=BO=ON=22,OC=CN2-ON2
6、=1,AC=22+1,BC=22-1.A=NMB,ANC=MBC,ACNMCB,ACCM=CNBC,ACBC=CMCN,7=3CM,CM=73.3.解析(1)由ACBD,得RtADE,在RtAED中,根据两个锐角互余,得CAD与ADE的关系;AB=AC,在等腰三角形ABC中,得BAC与底角ACB的关系;再结合同弧所对圆周角相等,得ADE=ACB,整理即可得出结论;(2)由DF=DC,得外角BDC与CFD的关系,再结合BAC=2DAC与同弧所对圆周角相等得CFD=CAD=CBD,得CF=BC,知CA垂直平分BF,求出AB与AC的长度,根据勾股定理列方程分别求出AE,CE,BE,再利用ADEBCE
7、,求出AD,DE,作ABD中AB边上的高DH,利用面积法求出DH,利用勾股定理求出AH的值,即可利用正切定义求值.解:(1)证明:ACBD,AED=90,在RtAED中,ADE=90-CAD,AB=AC,AB=AC,ACB=ABC.BAC=180-2ACB=180-2ADB=180-2(90-CAD),即BAC=2CAD.(2)DF=DC,FCD=CFD,BDC=FCD+CFD=2CFD.BDC=BAC,BAC=2CAD,CFD=CAD.CAD=CBD,CFD=CBD,CF=CB.ACBD,BE=EF,故CA垂直平分BF,AC=AB=AF=10,设AE=x,则CE=10-x,在RtABE和Rt
8、BCE中,AB2-AE2=BE2=BC2-CE2,又BC=45,102-x2=(45)2-(10-x)2,解得x=6,AE=6,CE=4,BE=AB2-AE2=8.DAE=CBE,ADE=BCE,ADEBCE,AEBE=DECE=ADBC,DE=3,AD=35,过点D作DHAB于H.SABD=12ABDH=12BDAE,BD=BE+DE=11,10DH=116,DH=335,在RtADH中,AH=AD2-DH2=65,tanBAD=DHAH=33565=112.4.解:(1)如图,连接PF.在RtABC中,由勾股定理得AC=BC2-AB2=102-62=8.设AP=x,则DP=10-x,PF=
9、x.P与边CD相切于点F,PFCD.四边形ABCD是平行四边形,ABCD.又ABAC,ACCD,PFAC,DPFDAC.PFAC=PDAD,即x8=10-x10.解得x=409,即AP=409.(2)409AP245或AP=55.解:(1)证明:连接BO并延长交AC于H,如图,由于O是ABC的外接圆,AB=BC,则BHAC且AH=CH.AB=CD,ABCD,四边形ABDC是平行四边形,ACBD,BHBD,即OBBD,BD是O的切线.(2)由(1)知,BD=AC,而AC=2AH=2ABcosBAC=21035=12,BD=12.设O的半径为r,OH=x,则有r+x=BH,AH2+x2=r2,又B
10、H=AB2-AH2=102-62=8,r+x=8,又由AH2+x2=r2得(r+x)(r-x)=AH2=36,r-x=92,联立,解得r=254,O的半径为254.6.解:(1)证明:如图,连接OD,DF是O的切线,ODEF,ODE=90.AC=BC,ABC=A.OD=OB,OBD=ODB,A=ODB,ODAC,CFE=ODE=90,DFAC.(2)如图,连接BG,BC是直径,BGC=90.在RtACD中,DC=AC2-AD2=52-32=4.ABCD=2SABC=ACBG,BG=ABCDAC=645=245,CG=BC2-BG2=52-(245)2=75.BGAC,EFAC,BGEF,E=C
11、BG,tanE=tanCBG=CGBG=724.7.解:(1)证明:在矩形ABCD中,ABO=OCE=90.OEOA,AOE=90,BAO+AOB=AOB+COE=90,BAO=COE,ABOOCE,ABOC=AOOE.OB=OC,ABOB=AOOE.ABO=AOE=90,ABOAOE,BAO=OAE,过O作OFAE于F,ABO=AFO=90,在ABO与AFO中,BAO=FAO,ABO=AFO,AO=AO,ABOAFO(AAS),OF=OB,AE是半圆O的切线.(2)连接PF,FC,延长FO交O于G,连接PG,则G=ACF,G+PFG=90,AF是O的切线,AFP+PFG=90,AFP=G=A
12、CF,FAP=CAF,AFPACF,AFAC=APAF,AF2=APAC,AF=2(2+4)=23,AB=AF=23,AC=6,BC=AC2-AB2=26,AO=AB2+OB2=32,ABOAOE,AOAE=ABAO,32AE=2332,AE=33.8.解:(1)证明:AB是O的直径,ACB=90.DEAB,DEO=90.DEO=ACB.ODBC,DOE=ABC,DOEABC.(2)证明:DOEABC,ODE=A.A和BDC是BC所对的圆周角,A=BDC,ODE=BDC,ODE-CDE=BDC-CDE,即ODF=BDE.(3)DOEABC,SDOESABC=ODAB2=14,即SABC=4SDOE=4S1.OA=OB,SBOC=12SABC,即SBOC=2S1.S1S2=27,S2=SBOC+SDOE+SDBE=2S1+S1+SDBE,SDBE=12S1,BE=12OE,即OE=23OB=23OD,sinA=sinODE=OEOD=23.
