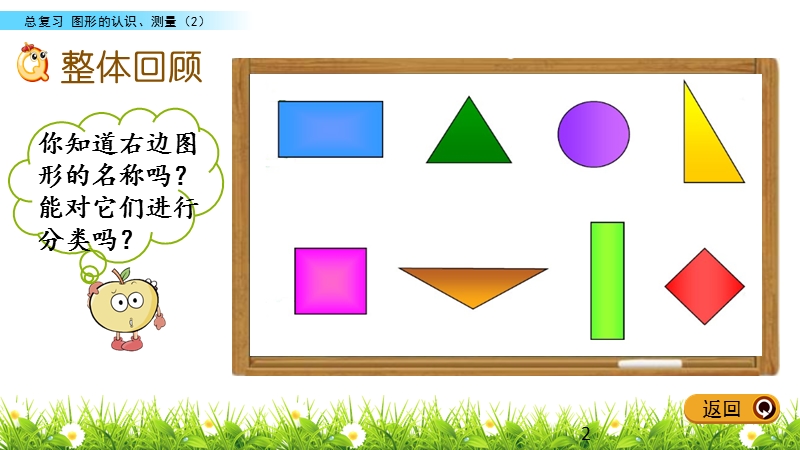
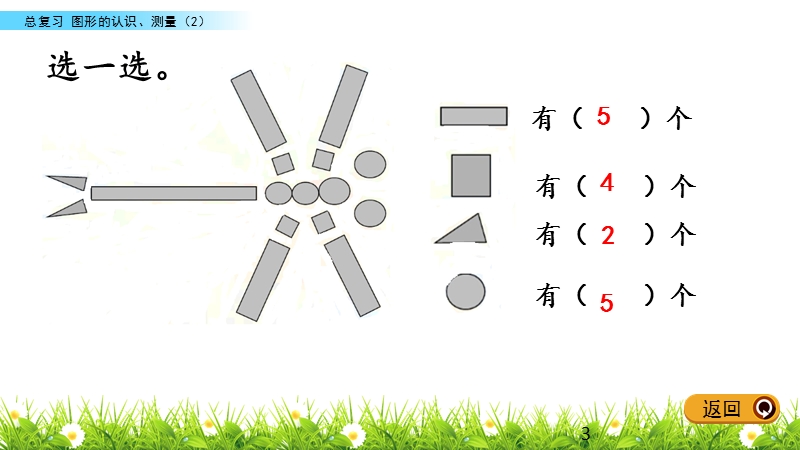
1、图形的测量、认识（2）,总复习,7,整体回顾,综合运用,课后作业,知识梳理,1,返回,整体回顾,2,返回,5,4,2,5,选一选。,3,返回,一个三角形两个内角的和是100，那么这个三角形是（ ）。 A.锐角三角形 B.钝角三角形 C.直角三角形 D.不确定是什么三角形 一个四边形的四条边分别是8厘米、6厘米、10厘米、6厘米。这个四边形可能是（ ）。 A.长方形 B.平行四边形 C.梯形 D.正方形,首先明确三角形的分类，再根据三角形的内角和是180来推断这个三角形是什么三角形。,注意记清长方形、正方形、平行四边形、梯形的定义哦。,D,C,4,返回,平面图形,知识梳理,5,返回,三角形：,1
2、.定义:,有三条线段首尾顺次相接围成的一个封闭的平面图形叫作三角形。,2.三角形各部分的名称。,围成三角形的三条线段叫作三角形的边，每两条边的交点叫作三角形的顶点，每两条边 所组成的角叫作三角形的内角。一个三角形有三条边、三个顶点和三个内角。,6,3.三角形的分类。,(1)按角分。,锐角三角形:三个角都是锐角的三角形。 直角三角形:有一一个角是直角的三角形。直角三角形的两个锐角的和是90,等腰直角三角形的两个锐角都是45。 钝角三角形：有一个角是钝角的三角形。,返回,7,返回,(2)按边分。,不等边三角形:三条边的长度都不相等的三角形。 等腰三角形和等边三角形。 a.等腰三角形:有两条边长度相
3、等的三角形。 b.等边三角形:三条边的长度都相等，三个内角都是60。 等边三角形是特殊的等腰三角形。,8,4.三角形的内角和都是180。,5.三角形的特性:三角形具有稳定性。,6.三角形边的关系:三角形的任意两边之和大于第三边。,返回,9,返回,四边形,四边形的意义：,四边形的分类及其关系：,在同一平面内，由四条线段首尾顺次相接围成的一个封闭的图形。,长方形和正方形是特殊的平行四边形,正方形是特殊的长方形， 直角梯形和等腰梯形都是特殊的梯形。,10,（3）平行四边形：,（2）正方形的特征：,（1）长方形的特征：,四边形的特性：,（4）梯形：,两组对边分别平行且相等，四个角都是直角。,四条边都相
4、等，四个角都是直角。,两组对边分别平行且相等，对角相等。,只有一组对边平行的四边形叫作梯形。平行的这一组对边叫作梯形的底，较短的一边叫上底，较长的一边叫下底。另一组边叫梯形的腰。 等腰梯形：两腰相等的梯形叫等腰梯形。 直角梯形：有两个角是直角的梯形。,返回,11,返回,圆,定义：,圆是一种封闭的曲线图形。,圆的各部分的名称：,(1)圆中心的一点叫作圆心。 圆心般用字母0表示。 (2)半径:连接圆心和圆上任意点的线段叫作半径。 半径一般用字母r表示。 (3)通过圆心并且两端都在圆上的线段叫作直径。直径一般用字母d表示。,12,圆的特征：,(1)在同一个圆里,有无数条半径和直径，每条半径的长度都相
5、等，每条直径长度也都相等。 (2)在同一个圆里，直径的长度是半径的2倍，半径的长度是直径的 。即d=2r或r= d。 (3)圆是轴对称图形，它有无数条对称轴。通过圆心的直线或直径所在的直线是圆的对称轴。 (4)圈心确定圆的位置， 半径决定圆的大小。,返回,13,返回,圆的画法：,把圆规的两脚分开，定好两脚间的距离（即半径），把有针尖的一只脚固定在一点（即圆心上），把装有铅笔尖的一只脚旋转一周，就画出一个圆。,圆周率：,圆周率:圆的周长总是直径的3倍多一些，这是一个固定的值，我们把它叫作圆周率用字母表示。圆周率是一个无限不循环小数，计算时一般保留两位小数，即值取3.14。,圆环,两个半径不等的同
6、心圆之间的部分叫作圆环。,定义：,14,（1） 直角三角形的一个锐角是 56， 另一个锐角 是（ ）。 （2） 等腰三角形的一个底角是 40， 顶角是（ ）。 （3） 三角形三个角度数的比是 2： 4： 3， 最大的角是（ ）。,填一填。,34,100,80,综合运用,返回,15,返回,围一个等腰三角形， 你准备 选哪三根小棒？ 为什么？,2厘米 2厘米 6厘米 6厘米,答：选2厘米、6厘米、6厘米。,利用三角形任意两边之和大于第三边的性质来选择小棒哦。,16,返回,在一个边长是9厘米的正方形中画一个最大的圆，这个圆的半径是多少厘米？,根据题意，可列式：9 ,=4.5（厘米）,答：这个圆的半径是4.5厘米。,在一个边长是9厘米的正方形中画一个最大的圆，就是以正方形的边长为圆的直径画圆，因此圆的半径是正方形边长的一半。,17,返回,课后作业,补充习题： 对应练习,18,
