1、2018-2019学年广东省深圳市宝安区八年级（下）期末数学试卷一、选择题（本题共有12小题，每小题3分，共36分，每小题有四个选项，其中只有一个是正确的）1（3分）下列各数中，能使不等式x20成立的是（）A6B5C4D22（3分）下列图形中，既是轴对称图形，又是中心对称图形的是（）ABCD3（3分）要使分式有意义，则x的取值范围是（）Ax3Bx3Cx3Dx34（3分）化简结果正确的是（）AxB1CD5（3分）已知正多边形的一个外角等于60，则该正多边形的边数为（）A3B4C5D66（3分）下列多项式中，可以使用平方差公式进行因式分解的是（）Ax2+1Bx2+1Cx2+xDx2+2x+17（3
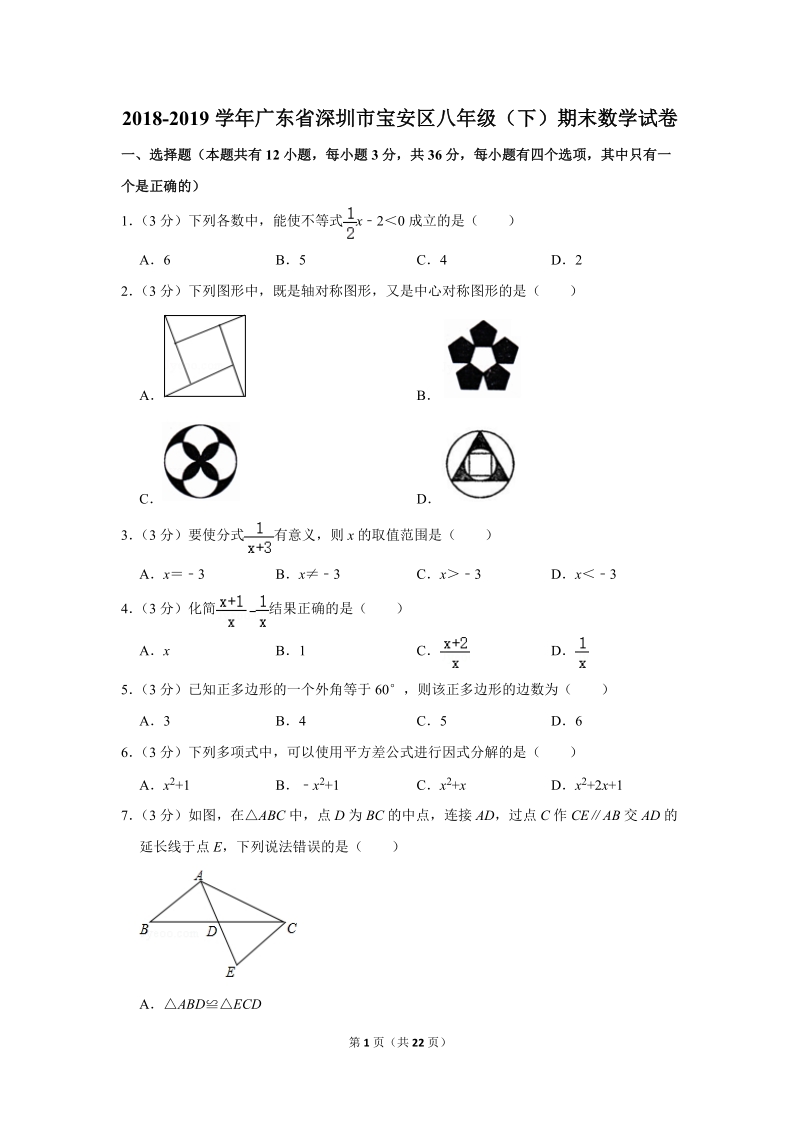
2、分）如图，在ABC中，点D为BC的中点，连接AD，过点C作CEAB交AD的延长线于点E，下列说法错误的是（）AABDECDB连接BE，四边形ABEC为平行四边形CDADEDCECA8（3分）如图，在ABC中，ABC的平分线交AC于点D，AD6，过点D作DEBC交AB于点E，若AED的周长为16，则边AB的长为（）A6B8C10D129（3分）下列命题中，正确的是（）A在三角形中，到三角形三边距离相等的点是三条边垂直平分线的交点B平行四边形是轴对称图形C三角形的中位线将三角形分成面积相等的两个部分D一组对边平行，一组对角相等的四边形是平行四边形10（3分）如图，在ABCD中，ACBD于点O，点E
3、为BC中点，连接OE，OE，则ABCD的周长为（）A4B6C8D1211（3分）如图，一次图数yx+3与一次函数y2x+m图象交于点（2，n），则关于x的不等式组的解集为（）Ax2Bx3C2x3D0x312（3分）如图，在ABC中，A90，ABAC，ABC的角平分线交AC于D，BD4，过点C作CEBD交BD的延长线于E，则CE的长为（）AB2C3D2二、填空题（每小题3分，共12分）13（3分）因式分解：2x22 14（3分）已知关于x的方程2x+mx3的根是正数，则m的取值范围是 15（3分）如图，点C为线段AB上一点，且CB1，分别以AC、BC为边，在AB的同一
4、侧作等边ACD和等边CBE，连接DE，AE，CDE30，则ADE的面积为 16（3分）如图1所示，在RtABC中，B90，AB4，BC3，将ABC沿着AC翻折得到ADC，如图2，将ADC绕着点A旋转到ADC，连接CD，当CDAB时，四边形ABCD的面积为 三、解答题（本题共7小题，第17题6分，第18题7分，第19题6分，第20题7分，第21题8分，第22、23题各9分，共52分）17（6分）解不等式组，并把它的解集在数轴上表示出来18（7分）先化简，再求值：，其中x119（6分）解方程：+120（7分）在ABC中，ABAC10，D为BC边上的中点，BD6，连接AD
5、（1）尺规作图：作AC边的中垂线交AD于点P；（保留作图痕迹，不要求写作法和证明）（2）连接CP，求DPC的周长21（8分）在ABCD中，点E为AB边的中点，连接CE，将BCE沿着CE翻折，点B落在点G处，连接AG并延长，交CD于F（1）求证：四边形AECF是平行四边形；（2）若CF5，GCE的周长为20，求四边形ABCF的周长22（9分）宝安区某街道对长为20千米的路段进行排水管道改造后，需对该段路面全部重新进行修整，甲、乙两个工程队将参与施工，已知甲队每天的工作效率是乙队的2倍，若由甲、乙两队分别单独修整长为800米的路面，甲队比乙队少用5天（1）求甲队每天可以修整路面多少米？（2）若街道
6、每天需支付给甲队的施工费用为0.4万元，乙队为0.25万元，如果本次路面修整预算55万元，为了不超出预算，至少应该安排甲队参与工程多少天？23（9分）如图，在平面直角坐标系中，直线l1：yx+2向下平移1个单位后，得到直线l2，l2交x轴于点A，点P是直线l1上一动点，过点P作PQy轴交l2于点Q（1）求出点A的坐标；（2）连接AP，当APQ为以PQ为底边的等腰三角形时，求点P和点Q的坐标；（3）点B为OA的中点，连接OQ、BQ，若点P在y轴的左侧，M为直线y1上一动点，当PQM与BOQ全等时，求点M的坐标2018-2019学年广东省深圳市宝安区八年级（下）期末数学试卷参考答案与试题解析一、选
7、择题（本题共有12小题，每小题3分，共36分，每小题有四个选项，其中只有一个是正确的）1（3分）下列各数中，能使不等式x20成立的是（）A6B5C4D2【分析】先求解不等式，再确定满足不等式的选项【解答】解：解不等式x20，得x4故选：D【点评】本题考查了一元一次不等式的解法会求解一元一次不等式是解决本题的关键2（3分）下列图形中，既是轴对称图形，又是中心对称图形的是（）ABCD【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解【解答】解：A、不是轴对称图形，是中心对称图形，故本选项错误；B、是轴对称图形，不是中心对称图形，故本选项错误；C、是轴对称图形，又是中心对称图形，故本
8、选项正确；D、是轴对称图形，不是中心对称图形，故本选项错误故选：C【点评】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合3（3分）要使分式有意义，则x的取值范围是（）Ax3Bx3Cx3Dx3【分析】本题主要考查分式有意义的条件：分母不能为0，即x+30，解得x的取值范围【解答】解：x+30，x3故选：B【点评】本题考查的是分式有意义的条件：当分母不为0时，分式有意义4（3分）化简结果正确的是（）AxB1CD【分析】根据分式的加减法法则计算即可得出正确选项【解答】解：故选：B【点评】本题主要考
9、查了分式的加减，同分母分式相加减，分母不变，分子相加减5（3分）已知正多边形的一个外角等于60，则该正多边形的边数为（）A3B4C5D6【分析】利用外角和360外角的度数即可得到边数【解答】解：360606故该正多边形的边数为6故选：D【点评】此题主要考查了多边形内角与外角，关键是掌握多边形外角和为3606（3分）下列多项式中，可以使用平方差公式进行因式分解的是（）Ax2+1Bx2+1Cx2+xDx2+2x+1【分析】根据提公因式法、平方差公式、完全平方公式进行因式分解，判断即可【解答】解：A、x2+1，不能进行因式分解；B、x2+11x2（1+x）（1x），可以使用平方差公式进行因式分解；C
10、、x2+xx（x+1），可以使用提公因式法进行因式分解；D、x2+2x+1（x+1）2，可以使用完全平方公式进行因式分解；故选：B【点评】本题考查的是因式分解，掌握提公因式法、平方差公式、完全平方公式进行因式分解的一般步骤是解题的关键7（3分）如图，在ABC中，点D为BC的中点，连接AD，过点C作CEAB交AD的延长线于点E，下列说法错误的是（）AABDECDB连接BE，四边形ABEC为平行四边形CDADEDCECA【分析】根据平行线的性质得出BDCE，BADE，然后根据AAS证得ABDECD，得出ADDE，根据对角线互相平分得到四边形ABEC为平行四边形，CEAB，即可解答【解答】解：CEA
11、B，BDCE，BADE，在ABD和ECD中，ABDECD（AAS），DADE，ABCE，ADDE，BDCD，四边形ABEC为平行四边形，故选：D【点评】本题考查了平行线的性质，三角形全等的判定和性质以及平行四边形的性判定，解决本题的关键是证明ABDECD8（3分）如图，在ABC中，ABC的平分线交AC于点D，AD6，过点D作DEBC交AB于点E，若AED的周长为16，则边AB的长为（）A6B8C10D12【分析】根据角平分线的定义得到EBDCBD，根据平行线的性质得到EDBCBD，等量代换得到EBDEDB，求得BEDE，于是得到结论【解答】解：BD平分ABC，EBDCBD，DEBC，EDBCB
12、D，EBDEDB，BEDE，AED的周长为16，AB+AD16，AD6，AB10，故选：C【点评】本题考查了平行线的性质，角平分线的性质，等腰三角形的判定和性质，熟练掌握各定理是解题的关键9（3分）下列命题中，正确的是（）A在三角形中，到三角形三边距离相等的点是三条边垂直平分线的交点B平行四边形是轴对称图形C三角形的中位线将三角形分成面积相等的两个部分D一组对边平行，一组对角相等的四边形是平行四边形【分析】由三角形的内心和外心性质得出选项A不正确；由平行四边形的性质得出选项B不正确；由三角形中位线定理得出选项C不正确；由平行四边形的判定得出选项D正确；即可得出结论【解答】解：A在三角形中，到三
13、角形三边距离相等的点是三条边垂直平分线的交点；不正确；B平行四边形是轴对称图形；不正确；C三角形的中位线将三角形分成面积相等的两个部分；不正确；D一组对边平行，一组对角相等的四边形是平行四边形；正确；故选：D【点评】本题考查了命题与定理、三角形的内心与外心、平行四边形的判定与性质以及三角形中位线定理；对各个命题进行正确判断是解题的关键10（3分）如图，在ABCD中，ACBD于点O，点E为BC中点，连接OE，OE，则ABCD的周长为（）A4B6C8D12【分析】在ABCD中，ACBD于点O，ABCD为菱形，则其四边相等，RtBOC中，点E为斜边BC中点，OEBEEC，从而可求ABCD的周长【解答
14、】解：ACBD，ABCD为菱形，则其四边相等且点E为斜边BC中点，OEBEEC，BC2，ABCD的周长4BC8故选：C【点评】本题主要考查平行四边形的性质，熟练掌握平行四边形的性质是解答本题的关键11（3分）如图，一次图数yx+3与一次函数y2x+m图象交于点（2，n），则关于x的不等式组的解集为（）Ax2Bx3C2x3D0x3【分析】先求出直线yx+3与x轴的交点坐标，然后根据函数特征，写出在x轴上，直线y2x+m在直线yx+3上方所对应的自变量的范围【解答】解：直线yx+3与x轴的交点坐标为（3，0），所以不等式组的解集为2x3故选：C【点评】本题考查了一次函数与一元一次不等式：从函数的角
15、度看，就是寻求使一次函数ykx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线ykx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合12（3分）如图，在ABC中，A90，ABAC，ABC的角平分线交AC于D，BD4，过点C作CEBD交BD的延长线于E，则CE的长为（）AB2C3D2【分析】延长CE与BA延长线交于点F，首先证明BADCAF，根据全等三角形的性质可得BDCF，再证明BEFBEC可得CEEF，进而可得CEBD，即可得出结果【解答】证明：延长CE与BA延长线交于点F，BAC90，CEBD，BACDEC，ADBCDE，ABDDCE，在BAD和CAF中
16、，BADCAF（ASA），BDCF，BD平分ABC，CEDB，FBECBE，在BEF和BEC中，BEFBEC（AAS），CEEF，DB2CE，即CEBD42，故选：B【点评】本题考查了全等三角形的判定与性质、角平分线定义，熟练掌握全等三角形的判定方法，全等三角形对应边相等是解题的关键二、填空题（每小题3分，共12分）13（3分）因式分解：2x222（x+1）（x1）【分析】首先提公因式2，再利用平方差进行二次分解【解答】解：原式2（x21）2（x+1）（x1）故答案为：2（x+1）（x1）【点评】此题主要考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果
17、可以先提取公因式的要先提取公因式，再考虑运用公式法分解14（3分）已知关于x的方程2x+mx3的根是正数，则m的取值范围是m3【分析】根据关于x的方程2x+mx3的根是正数，可以求得m的取值范围【解答】解：由方程2x+mx3，得xm3，关于x的方程2x+mx3的根是正数，m30，解得，m3，故答案为：m3【点评】本题考查解一元一次方程和一元一次不等式，解答本题的关键是明确题意，求出m的取值范围15（3分）如图，点C为线段AB上一点，且CB1，分别以AC、BC为边，在AB的同一侧作等边ACD和等边CBE，连接DE，AE，CDE30，则ADE的面积为【分析】由等边三角形的性质得出CECB1，ADC
18、D，DCAECBADC60，由平角的定义得出DCE60，由三角形内角和定理得出CED90，由含30角的直角三角形的性质得出CECD，即ADCD2CE2，DECDsin602，ADEADC+CDE90，则SADEADDE，即可得出结果【解答】解：ACD和CBE都是等边三角形，CECB1，ADCD，DCAECBADC60，DCE180DCAECB180606060，CDE30，CED180CDEDCE180306090，CECD，即ADCD2CE2，DECDsin602，ADEADC+CDE60+3090，SADEADDE2，故答案为：【点评】本题考查了等边三角形的性质、三角形内角和定理、含30角
19、直角三角形的性质、三角形面积的计算等知识，熟练掌握等边三角形的性质，证明三角形是含30角直角三角形是解题的关键16（3分）如图1所示，在RtABC中，B90，AB4，BC3，将ABC沿着AC翻折得到ADC，如图2，将ADC绕着点A旋转到ADC，连接CD，当CDAB时，四边形ABCD的面积为【分析】过点A作AEAB交CD的延长线于E，构造直角三角形，利用勾股定理即可【解答】解：如图（2），过点A作AEAB交CD的延长线于E，由翻折得ADAB4CDABBCE+ABC180，ABC90BCE90AEABBAE90ABCE是矩形，ADADAB4AEBC3，CEAB4，AEC90DECDCEDE4S四边
20、形ABCD（AB+CD）BC（4+4）3，故答案为：【点评】本题考查了勾股定理，矩形性质，翻折、旋转的性质，梯形面积等，解题关键对翻折、旋转几何变换的性质要熟练掌握和运用三、解答题（本题共7小题，第17题6分，第18题7分，第19题6分，第20题7分，第21题8分，第22、23题各9分，共52分）17（6分）解不等式组，并把它的解集在数轴上表示出来【分析】分别解两个不等式，找其公共部分就是不等式组的解集【解答】解：解不等式得：x2，解不等式得：x2，故不等式得解集为：x2，在数轴上表示为：【点评】本题考查了解一元一次不等式组及其在数轴上表示不等式的解集，解题的关键掌握找不等式组公共部分的法则：
21、同大取大，同小取小，大小小大中间找，大大小小找不了18（7分）先化简，再求值：，其中x1【分析】先算括号里面的加法，再将除法转化为乘法，将结果化为最简，然后把x的值代入进行计算即可【解答】解：原式，当x1时，原式【点评】此题考查了分式的混合运算化简求值，熟练掌握运算法则是解本题的关键19（6分）解方程：+1【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解【解答】解：去分母得：1+x2x1，解得：x0，经检验x0是分式方程的解【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解解分式方程一定注意要验根20（7分
22、）在ABC中，ABAC10，D为BC边上的中点，BD6，连接AD（1）尺规作图：作AC边的中垂线交AD于点P；（保留作图痕迹，不要求写作法和证明）（2）连接CP，求DPC的周长【分析】（1）利用基本作图作AC的垂直平分线得到点P；（2）根据线段垂直平分线的性质得到PAPC，则利用等线段代换得到DPC的周长DA+DC，再根据等腰三角形的性质得到ADBC，利用勾股定理计算出AD8，从而可计算出DPC的周长【解答】解：（1）如图，点D为所作；（2）AC边的中垂线交AD于点P，PAPC，DPC的周长DP+DC+PCDP+PA+DCDA+DC，ABAC10，D为BC边上的中点，ADBC，CDBD6，AD
23、8，DPC的周长8+614【点评】本题考查了作图基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）也考查了等腰三角形的性质21（8分）在ABCD中，点E为AB边的中点，连接CE，将BCE沿着CE翻折，点B落在点G处，连接AG并延长，交CD于F（1）求证：四边形AECF是平行四边形；（2）若CF5，GCE的周长为20，求四边形ABCF的周长【分析】（1）由平行四边形的性质得出AEFC，再由三角形的外角的性质，以及折叠的性质，可以证明FAECEB，进而证明AFEC，即可得出结论；（2）由折叠的性质得：GEBE
24、，GCBC，由GCE的周长得出GE+CE+GC20，BE+CE+BC20，由平行四边形的性质得出AFCE，AECF5，即可得出结果【解答】（1）证明：四边形ABCD是平行四边形，AEFC，点E是AB边的中点，AEBE，将BCE沿着CE翻折，点B落在点G处，BEGE，CEBCEG，AEGE，FAEAGE，CEBCEGBEG，BEGFAE+AGE，FAEBEG，FAECEB，AFEC，四边形AECF是平行四边形；（2）解：由折叠的性质得：GEBE，GCBC，GCE的周长为20，GE+CE+GC20，BE+CE+BC20，四边形AECF是平行四边形，AFCE，AECF5，四边形ABCF的周长AB+B
25、C+CF+AFAE+BE+BC+CE+CF5+20+530【点评】本题主要考查了翻折变换的性质、平行四边形的判定与性质、平行线的判定、等腰三角形的性质以及三角形的外角性质等知识；熟练掌握翻折变换的性质，证明四边形AECF是平行四边形是解题的关键22（9分）宝安区某街道对长为20千米的路段进行排水管道改造后，需对该段路面全部重新进行修整，甲、乙两个工程队将参与施工，已知甲队每天的工作效率是乙队的2倍，若由甲、乙两队分别单独修整长为800米的路面，甲队比乙队少用5天（1）求甲队每天可以修整路面多少米？（2）若街道每天需支付给甲队的施工费用为0.4万元，乙队为0.25万元，如果本次路面修整预算55万
26、元，为了不超出预算，至少应该安排甲队参与工程多少天？【分析】（1）设甲队每天可以修整路面x米，则乙队每天可以修整路面x米，根据“甲、乙两队分别单独修整长为800米的路面，甲队比乙队少用5天”列出方程并解答；（2）设应该安排甲队参与工程y天，根据“每天需支付给甲队的施工费用为0.4万元，乙队为0.25万元，如果本次路面修整预算5.5万元”列出不等式并解答【解答】解：（1）设甲队每天可以修整路面x米，则乙队每天可以修整路面x米，根据题意，得+5解得x160经检验，x160是原方程的根，且符合题意答：甲队每天可以修整路面160米；（2）设应该安排甲队参与工程y天，根据题意，得0.4y+0.2555解
27、得y75故至少应该安排甲队参与工程75天，【点评】本题考查分式方程的应用，一元一次不等式的应用，分析题意，找到合适的等量关系和不等关系是解决问题的关键23（9分）如图，在平面直角坐标系中，直线l1：yx+2向下平移1个单位后，得到直线l2，l2交x轴于点A，点P是直线l1上一动点，过点P作PQy轴交l2于点Q（1）求出点A的坐标；（2）连接AP，当APQ为以PQ为底边的等腰三角形时，求点P和点Q的坐标；（3）点B为OA的中点，连接OQ、BQ，若点P在y轴的左侧，M为直线y1上一动点，当PQM与BOQ全等时，求点M的坐标【分析】（1）求出直线l2的解析式为yx+1，即可求A的坐标；（2）设点P（
28、x，x+2），Q（x，x+1），由AQAP，即可求P点坐标；（3）设P（n，n+2），M（m，1），则Q（n，n+1），可求出BQ，OQ，PM，QM，当PQMBOQ时，PMBQ，QMOQ，求出M；当PQMBOQ时，有PMBQ，QMOQ，求出M即可【解答】解：（1）直线l1：yx+2向下平移1个单位后，得到直线l2，直线l2的解析式为yx+1，l2交x轴于点A，A（2，0）；（2）当APQ为以PQ为底边的等腰三角形时，AQAP，点P是直线l1上一动点，设点P（x，x+2），过点P作PQy轴交l2于点QQ（x，x+1），（x+2）2（x+1）2，x3，P（3，），Q（3，）；（3）点B为OA的中点，B（1，0），PQBO1，设P（n，n+2），M（m，1），则Q（n，n+1），BQ，OQ，PM，QM，PQM与BOQ全等，当PQMBOQ时，有PMBQ，QMOQ，n4，m1或m7，M（1，1）或M（7，1）；当QPMBOQ时，有PMOQ，QMBQ，n，点P在y轴的左侧，n0，此时M不存在；综上所述，M（1，1）或M（7，1）【点评】本题考查一次函数的综合；熟练掌握一次函数的图象特点，等腰三角形与全等三角形的性质是解题的关键
