 2020年冀教新版九年级上册数学《第23章数据分析》单元测试卷(解析版)
2020年冀教新版九年级上册数学《第23章数据分析》单元测试卷(解析版)
《2020年冀教新版九年级上册数学《第23章数据分析》单元测试卷(解析版)》由会员分享,可在线阅读,更多相关《2020年冀教新版九年级上册数学《第23章数据分析》单元测试卷(解析版)(22页珍藏版)》请在七七文库上搜索。
1、2020年冀教新版九年级上册数学第23章 数据分析单元测试卷一选择题(共10小题)1为了了解某校300名初三学生的睡眠时间,从中抽取30名学生进行调查,在这个问题中,下列说法正确的是()A300名学生是总体B300是众数C30名学生是抽取的一个样本D30是样本的容量2为了了解2016年扬州市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩下列说法正确的是()A2016年扬州市九年级学生是总体B每一名九年级学生是个体C1000名九年级学生是总体的一个样本D样本容量是10003为了了解我市50000名学生参加初中毕业考试数学成绩情况,从中抽取了1000名考生的成绩进行统计下
2、列说法:这50000名学生的数学考试成绩的全体是总体;每个考生是个体;1000名考生是总体的一个样本;样本容量是1000其中说法正确的有()A4个B3个C2个D1个4在一个有15万人的小镇,随机调查了3000人,其中有300人看中央电视台的早间新闻据此,估计该镇看中央电视台早间新闻的约有()A2.5万人B2万人C1.5万人D1万人5青蛙是我们人类的朋友,为了了解某池塘里青蛙的数量,先从池塘里捕捞20只青蛙,作上标记后放回池塘,经过一段时间后,再从池塘中捕捞出40只青蛙,其中有标记的青蛙有4只,请你估计一下这个池塘里有多少只青蛙?()A100只B150只C180只D200只6有一组数据:2,5,
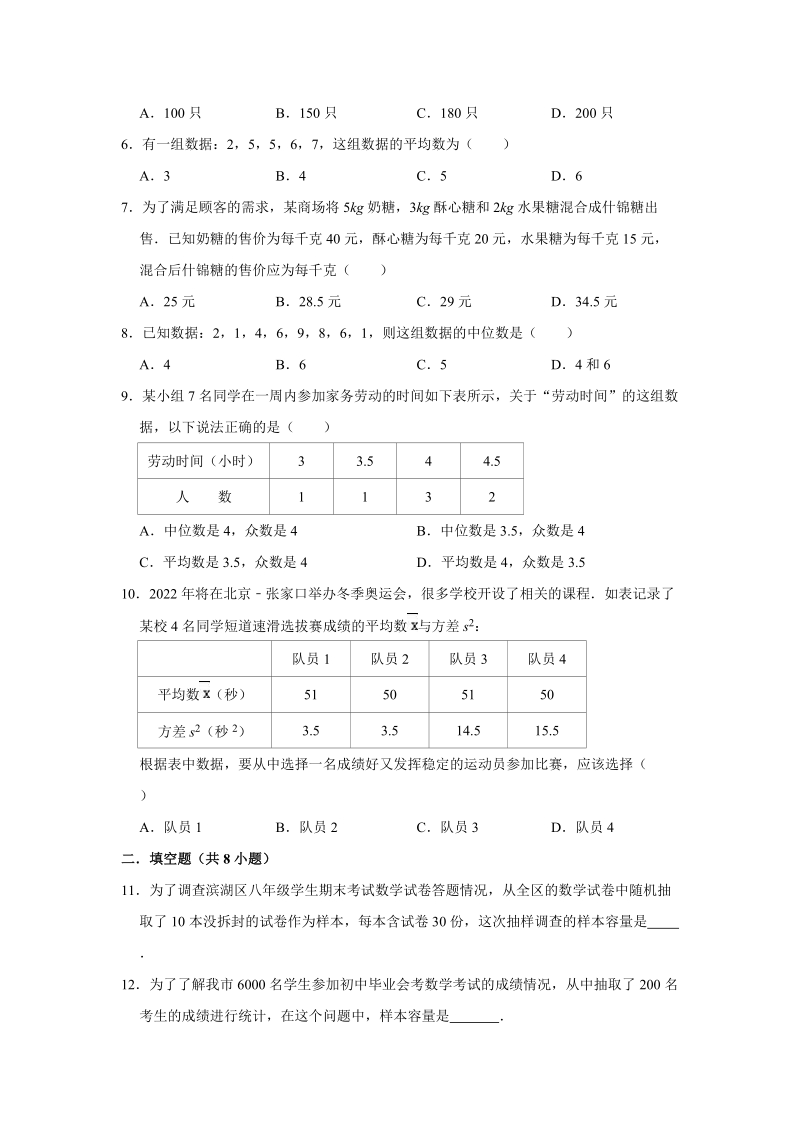
3、5,6,7,这组数据的平均数为()A3B4C5D67为了满足顾客的需求,某商场将5kg奶糖,3kg酥心糖和2kg水果糖混合成什锦糖出售已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,混合后什锦糖的售价应为每千克()A25元B28.5元C29元D34.5元8已知数据:2,1,4,6,9,8,6,1,则这组数据的中位数是()A4B6C5D4和69某小组7名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是()劳动时间(小时)33.544.5人数1132A中位数是4,众数是4B中位数是3.5,众数是4C平均数是3.5,众数是4D平均数是4
4、,众数是3.5102022年将在北京张家口举办冬季奥运会,很多学校开设了相关的课程如表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差s2:队员1队员2队员3队员4平均数(秒)51505150方差s2(秒2)3.53.514.515.5根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择()A队员1B队员2C队员3D队员4二填空题(共8小题)11为了调查滨湖区八年级学生期末考试数学试卷答题情况,从全区的数学试卷中随机抽取了10本没拆封的试卷作为样本,每本含试卷30份,这次抽样调查的样本容量是 12为了了解我市6000名学生参加初中毕业会考数学考试的成绩情况,从中抽取了200
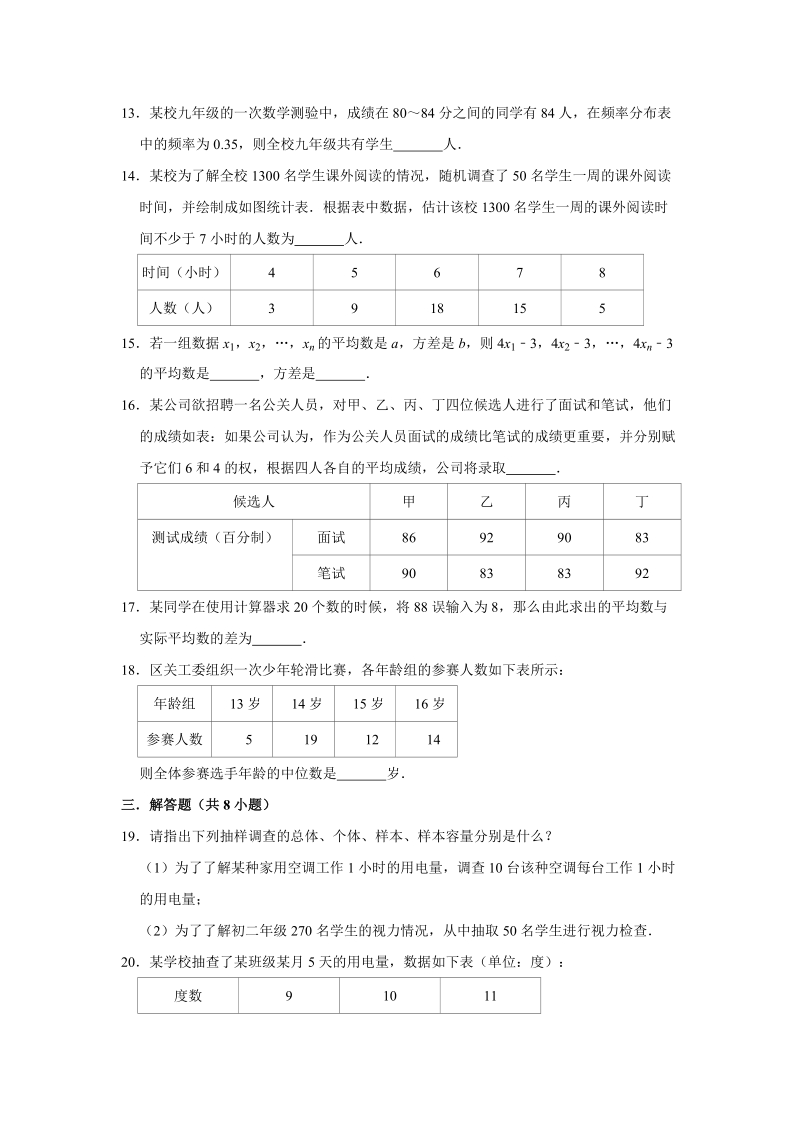
5、名考生的成绩进行统计,在这个问题中,样本容量是 13某校九年级的一次数学测验中,成绩在8084分之间的同学有84人,在频率分布表中的频率为0.35,则全校九年级共有学生 人14某校为了解全校1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图统计表根据表中数据,估计该校1300名学生一周的课外阅读时间不少于7小时的人数为 人时间(小时)45678人数(人)391815515若一组数据x1,x2,xn的平均数是a,方差是b,则4x13,4x23,4xn3的平均数是 ,方差是 16某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:如
6、果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,根据四人各自的平均成绩,公司将录取 候选人甲乙丙丁测试成绩(百分制)面试86929083笔试9083839217某同学在使用计算器求20个数的时候,将88误输入为8,那么由此求出的平均数与实际平均数的差为 18区关工委组织一次少年轮滑比赛,各年龄组的参赛人数如下表所示:年龄组 13岁 14岁 15岁 16岁参赛人数 5 19 12 14则全体参赛选手年龄的中位数是 岁三解答题(共8小题)19请指出下列抽样调查的总体、个体、样本、样本容量分别是什么?(1)为了了解某种家用空调工作1小时的用电量,调查10台该种空调每台
7、工作1小时的用电量;(2)为了了解初二年级270名学生的视力情况,从中抽取50名学生进行视力检查20某学校抽查了某班级某月5天的用电量,数据如下表(单位:度):度数91011天数311(1)求这5天的用电量的平均数;(2)求这5天用电量的众数、中位数;(3)学校共有36个班级,若该月按22天计,试估计该校该月的总用电量21据省环保网发布的消息,吉首市空气质量评价连续两年居全省14个省辖市城市之最,下表是吉首市2014年5月份前10天的空气质量指数统计表 (一)2014年5月1日10日空气质量指数(AQI)情况日期1日2日3日4日5日6日7日8日9日10日空气质量指数(AQI)283894536
8、314953908435(二)空气质量污染指数标准(AQI)污染指数 等级 050优51100良101150轻微污染151200轻度污染(1)请你计算这10天吉首市空气质量指数的平均数,并据此判断这10天吉首市空气质量平均情况属于哪个等级;(用科学计算器计算或笔算,结果保留整数)(2)按规定,当空气质量指数AQI100时,空气质量才算“达标”,请你根据表(一)和表(二)所提供的信息,估计今年(365天)吉首市空气质量“达标”的天数(结果保留整数)22在对全市初中生进行的体质健康测试中,青少年体质研究中心随机抽取的10名学生的坐位体前屈的成绩(单位:厘米)如下:11.2,10.5,11.4,10
9、.2,11.4,11.4,11.2,9.5,12.0,10.2(1)通过计算,样本数据(10名学生的成绩)的平均数是10.9,中位数是 ,众数是 ;(2)一个学生的成绩是11.3厘米,你认为他的成绩如何?说明理由;(3)研究中心确定了一个标准成绩,等于或大于这个成绩的学生该项素质被评定为“优秀”等级,如果全市有一半左右的学生能够达到“优秀”等级,你认为标准成绩定为多少?说明理由23八年级(1)班数学活动选出甲、乙两组各10名学生,进行趣味数学抢答比赛,共10道题,答对8题(含8题)以上为优秀,答对题数统计如下:答对题数5678910平均数中位数众数方差优秀率甲组1015218881.680%乙
10、组004321 请你完成上表,并根据所学的统计知识,从不同方面评价甲、乙两组选手的成绩24某公司招聘一名公关人员,应聘者小王参加面试和笔试,成绩(100分制)如表所示:面试笔试成绩评委1评委2评委392889086(1)请计算小王面试平均成绩;(2)如果面试平均成绩与笔试成绩按6:4的比确定,请计算出小王的最终成绩25甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)甲厂:4,5,5,5,5,7,9,12,13,15乙厂:6,6,8,8,8,9,10,12,14,15丙厂:4
11、,4,4,6,7,9,13,15,16,16请回答下列问题:(1)分别求出以上三组数据的平均数、众数、中位数;(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数;(3)如果你是顾客,宜选购哪家工厂的产品?为什么?26某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:17 18 16 13 24 15 28 26 18 1922 17 16 19 32 30 16 14 15 2615 32 23 17 15 15 28 28 16 19频数分布
12、表组别一二三四五六七销售额13x1616x1919x2222x2525x2828x3131x34频数793a2b2数据分析表平均数众数中位数20.3c18请根据以上信息解答下列问题:(1)填空:a ,b ,c ;(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员拿不到奖励;(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由2020年冀教新版九年级上册数学第23章 数据分析单元测试卷参考答案与试题解析一选择题(共10小题)1为了了解某校300名初三学生的睡眠时间,从中抽取30名学生进行调查,在这个问题中,下列说法正确的是()A300名学生是总体B300
13、是众数C30名学生是抽取的一个样本D30是样本的容量【分析】样本的容量指一个样本所含个体的数目即抽取学生的数量是样本的容量【解答】解:本题中总体是某校300名初三学生的睡眠时间,样本是抽取的30名学生的睡眠时间,故样本的容量是30所以A,B,C都错,D对故选:D【点评】掌握总体,样本,样本的容量以及众数的概念2为了了解2016年扬州市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩下列说法正确的是()A2016年扬州市九年级学生是总体B每一名九年级学生是个体C1000名九年级学生是总体的一个样本D样本容量是1000【分析】总体是指考查的对象的全体,个体是总体中的每一个考
14、查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象从而找出总体、个体再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量【解答】解:A、2016年扬州市九年级学生学业水平考试的数学成绩是总体,故A不符合题意;B、每名学生学业水平考试的数学成绩是个体,故B不符合题意;C、从中随机抽取了1000名学生的数学成绩是一个样本,故C不符合题意;D、样本容量是1000,故D符合题意;故选:D【点评】考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象总体、
15、个体与样本的考查对象是相同的,所不同的是范围的大小样本容量是样本中包含的个体的数目,不能带单位3为了了解我市50000名学生参加初中毕业考试数学成绩情况,从中抽取了1000名考生的成绩进行统计下列说法:这50000名学生的数学考试成绩的全体是总体;每个考生是个体;1000名考生是总体的一个样本;样本容量是1000其中说法正确的有()A4个B3个C2个D1个【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象从而找出总体、个体再根据被收集数据的这一部
16、分对象找出样本,最后再根据样本确定出样本容量【解答】解:这50000名学生的数学考试成绩的全体是总体,说法正确;每个考生是个体,说法错误,应该是每个考生的数学成绩是个体;1000名考生是总体的一个样本,说法错误,应是1000名考生的数学成绩是总体的一个样本;样本容量是1000,说法正确;正确的说法共2个,故选:C【点评】此题主要考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象总体、个体与样本的考查对象是相同的,所不同的是范围的大小样本容量是样本中包含的个体的数目,不能带单位4在一个有15万人的小镇,随机调查了3000人,其中有300人看中央电视台的
17、早间新闻据此,估计该镇看中央电视台早间新闻的约有()A2.5万人B2万人C1.5万人D1万人【分析】求得调查样本的看早间新闻的百分比,然后乘以该镇总人数即可【解答】解:该镇看中央电视台早间新闻的约有151.5万,故选:C【点评】本题考查了用样本估计总体的知识,解题的关键是求得样本中观看的百分比,难度不大5青蛙是我们人类的朋友,为了了解某池塘里青蛙的数量,先从池塘里捕捞20只青蛙,作上标记后放回池塘,经过一段时间后,再从池塘中捕捞出40只青蛙,其中有标记的青蛙有4只,请你估计一下这个池塘里有多少只青蛙?()A100只B150只C180只D200只【分析】从池塘中捕捞出40只青蛙,其中有标记的青蛙
18、有4只,即在样本中有标记的所占比例为,而在整体中有标记的共有20只,根据所占比例即可解答【解答】解:从池塘中捕捞出40只青蛙,其中有标记的青蛙有4只,在样本中有标记的所占比例为,池塘里青蛙的总数为20200故选:D【点评】此题主要考查了用样本去估计总体,统计的思想就是用样本的信息来估计总体的信息6有一组数据:2,5,5,6,7,这组数据的平均数为()A3B4C5D6【分析】把给出的这5个数据加起来,再除以数据个数5,就是此组数据的平均数【解答】解:(2+5+5+6+7)52555答:这组数据的平均数是5故选:C【点评】此题主要考查了平均数的意义与求解方法,关键是把给出的这5个数据加起来,再除以
19、数据个数57为了满足顾客的需求,某商场将5kg奶糖,3kg酥心糖和2kg水果糖混合成什锦糖出售已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,混合后什锦糖的售价应为每千克()A25元B28.5元C29元D34.5元【分析】先求出买5kg奶糖,3kg酥心糖和2kg水果糖的总钱数,再除以总的千克数,即可得出混合后什锦糖的售价【解答】解:根据题意得:(405+203+152)(5+3+2)29(元),答:混合后什锦糖的售价应为每千克29元故选:C【点评】此题考查了加权平均数,掌握加权平均数的计算公式是解题的关键,是一道基础题8已知数据:2,1,4,6,9,8,6,1,则这组
20、数据的中位数是()A4B6C5D4和6【分析】要求中位数,是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可,本题是最中间的两个数的平均数【解答】解:从小到大排列此数据为:1、1、2、4、6、6、8、9,第4位和第5位分别是4和6,平均数是5,则这组数据的中位数是5故选:C【点评】此题考查了中位数;注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数9某小组7名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是()劳动时间(小时)33.5
21、44.5人数1132A中位数是4,众数是4B中位数是3.5,众数是4C平均数是3.5,众数是4D平均数是4,众数是3.5【分析】根据众数和中位数的概念求解【解答】解:这组数据中4出现的次数最多,众数为4,共有7个人,第4个人的劳动时间为中位数,所以中位数为4,故选:A【点评】本题考查众数与中位数的意义,一组数据中出现次数最多的数据叫做众数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错102022年将在北京张家口举办冬季奥运会,很多学校开设了相关的课程如表记录了某校4

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 第23章数据分析 2020 年冀教 新版 九年级 上册 数学 23 数据 分析 单元测试 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-117721.html