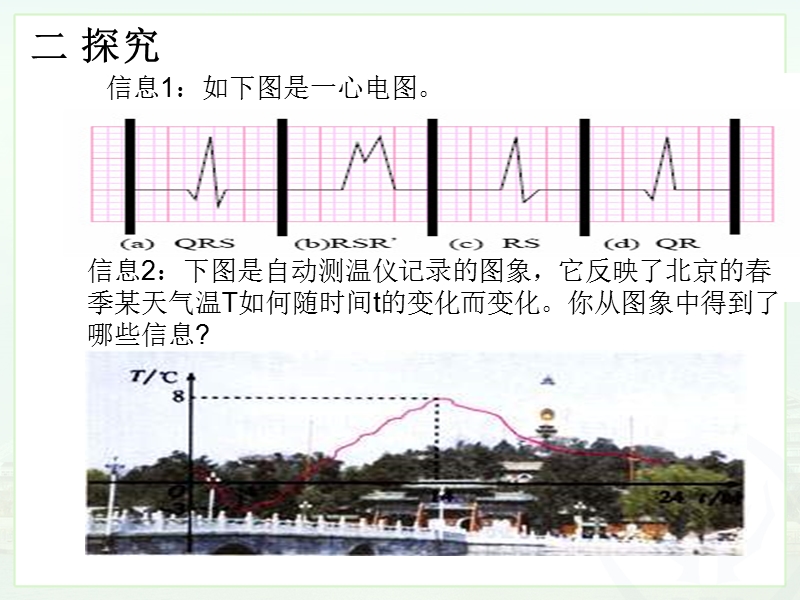
1、19.1.2 函数的图象（1）,1了解函数图象的意义；,2会观察函数图象获取信息，根据图象初步,分析函数的对应关系和变化规律,1经历画函数图象的过程，分别用点的横、,纵坐标表示自变量和对应的函数值,学习目标：,2会判断一个点是否在函数的图象上,一导学,学习重点：,学习难点：,信息1：如下图是一心电图。,信息2：下图是自动测温仪记录的图象，它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?,二 探究,我们先来思考这样一个问题：,正方形的边长x与面积S的函数关系为 , 其中自变量x的取值范围是 。,x 0,因为x表示的实际含义是正方形的边长， 边长只能为正。,你能解释
2、x0这个范围是怎样确定的吗？,计算并填写下表：,0,0.25,1,2.25,4,6.25,9,如果我们在直角坐标系中，将你所填表格中的自变量x及对应的函数值S当作一个点的横坐标与纵坐标，即可在坐标系中得到一些点。,0,0.25,1,2.25,4,6.25,9,用空心圈表示不在曲线上的点,S=x2(x0),这样我们就得到了一幅表示S与x关系的图,如点(2，4)表示x=2时S=4。,图中每个点都代表x的值与S的值的一种对应关系。,函数的图象,对于一个 ， 如果把 与 的 分别作为点的 ，那么坐标平面内由这些 组成的图形，就是这个函数的图象。,自变量,函数,每对对应值,横、纵坐标,点,函数,函数图象
3、可以数形结合地研究函数，给我们带来便利。,上图中的曲线即为函数 (x0)的图象,1、函数图象上点的横、纵坐标分别对应 值和 的值。,自变量,函数,2、从函数图象中获得的信息来研究实际问题关键要注意分清横轴和纵轴表示的,实际含义,下图是自动测温仪记录的图象，它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?,尝试运用：,横坐标表示 ，纵坐标表示 ,随 的变化而变化?,-3,时间,温度,时间,温度T,时间t,T/,北京春季某天气温 T 随时间 t 变化而变化的规律如图所示：,O,t/h,1.哪个时间温度最高？是多少度？,2.哪个时间温度最低？是多少度？,3.什么时间段
4、温度在下降？什么时间段温度在上升？,4.温度在零度以下的时间长呢？还是在零度以上的时间长？,24,5.曲线与x轴的交点表示什么？,1.在_点和_点的时候,两地气温相同; 2.在_点到_点和_点到_点之间, 上海的气温比北京的气温要高. 3.在_点到_点之间,上海的气温比北京的气温要低.,7,12,7,12,0 7,12 24,基础训练,例1下图反映的过程是小明从家去食堂吃早餐，接着去图书馆读报， 然后回家其中x 表示时间，y 表示小明离家的距离，小明家、 食堂、图书馆在同一直线上,根据图象回答下列问题： （1）食堂离小明家多远？小明从家到食堂用了多少时间？,学科网,典题讲解,例1 下图反映的过
5、程是小明从家去食堂吃早餐， 接着去图书馆读报，然后回家其中x 表示时间，y 表 示小明离家的距离，小明家、食堂、图书馆在同一直线 上,根据图象回答下列问题： （2）小明在食堂吃早餐用了多少时间？,例1 下图反映的过程是小明从家去食堂吃早餐， 接着去图书馆读报，然后回家其中x 表示时间，y 表 示小明离家的距离，小明家、食堂、图书馆在同一直线 上,根据图象回答下列问题： （3）食堂离图书馆多远？小明从食堂到图书馆用了多 少时间？,例1 下图反映的过程是小明从家去食堂吃早餐， 接着去图书馆读报，然后回家其中x 表示时间，y 表 示小明离家的距离，小明家、食堂、图书馆在同一直线 上,根据图象回答下列
6、问题： （4）小明读报用了多长时间？,例1 下图反映的过程是小明从家去食堂吃早餐， 接着去图书馆读报，然后回家其中x 表示时间，y 表 示小明离家的距离，小明家、食堂、图书馆在同一直线 上,根据图象回答下列问题： （5）图书馆离小明家多远？小明从图书馆回家的平均 速度是多少？,1.如果A、B两人在一次百米赛跑中，路程s（米） 与赛跑的时间t（秒）的关系如图所示，则下列说 法正确的是（ ） （A） A比B先出发 （B） A、B两人的速度相同 （C） A先到达终点 （D） B比A跑的路程多,2.某人早上进行登山活动，从山脚到山顶休息一会儿又沿原路返回，若用横轴表示时间t，纵轴表示与山脚距离h，那么
7、下列四个图中反映全程h与t的关系图是（ ）,C,D,课堂练习,3小芳今天到学校参加初中毕业会考，从家里出发走10分到离家500米的地方吃早餐，吃早餐用了20分；再用10分赶到离家1000米的学校参加考试下列图象中，能反映这一过程的是（ ） ,D,4某装水的水池按一定的速度放掉水池的一半后，停止放水并立即按一定的速度注水，水池注满后，停止注水，又立即按一定的速度放完水池的水。若水池的存水量为v（立方米），放水或注水的时间为t（分钟），则v与t的关系的大致图象只能是（ ）,A,5一枝蜡烛长20厘米，点燃后每小时燃烧掉5厘米，则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h（厘米）与点燃时间t
8、之间的函数关系的是（ ）.,C,6.小明从家里出发，外出散步，到一个公共阅报栏前看了一会报后，继续散步了一段时间，然后回家.下面的图描述了小明在散步过程中离家的距离s（米）与散步所用时间t（分）之间的函数关系.请你由图具体说明小明散步的情况.,小明先走了约3分钟，到达离家250米处的一个阅报栏前看了5分钟报，又向前走了2分钟，到达离家450米处返回，走了6分钟到家。,解：,7.甲，乙两同学骑自行车从地沿同一条路到地，已知 乙比甲先出发他们离出发地的距离skm和骑行时间 t/h之间的函数关系如图所示，给出下列说法： a.他们都骑了km； b.乙在途中停留了.h； c.甲和乙两人同时到达目的地；
9、d.甲乙两人途中没有相遇过 根据图象信息，以上说法正确的是 （ ）,s/km,t/h,A.1个,B.个,D.个,C.个,甲,乙,龟兔赛跑,8.领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉, 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已 经来不及了,乌龟先到达了终点现在用 和 分别表示乌龟、兔子所走的路程，t为时间，则下列 图象中，能够表示S 和t之间的函数关系式的是（ ）,A,B,D,C,C,例2 在下列式子中，对于x的每个确定的值。y有唯一的对应值，即y是x的函数请画出这些函数的图象。,解：,x取值范围是全体实数值， 列表如下：,-2.5,-1.5,-0.5,0.5,1.5,2.5
10、,根据表中数值描点(x，y)，并用光滑曲线连接这些点,从函数图象可以看出，直线从左向右上升，即当x由小变大时，y=x+0.5随之增大,自变量的取值范围x0 列表:,12,6,4,3,2.4,2,1.5,据表中数值描点(x, y)并用光滑曲线连结这些点，就得到图象,从函数图象可以看出，曲线从左向右下降，即当x由小变大时， 随之减小,我们来总结归纳一下描点法画函数图象的一般步骤,第一步：列表在自变量取值范围内选定一些值通过函数关系式求出对应函数值列成表格,第二步：描点在直角坐标系中，以自变量的值为横坐标，相应函数值为纵坐标，描出表中对应各点,第三步：连线按照坐标由小到大的顺序把所有点用平滑曲线连接
11、起来,1.小颖从家出发，直走了20分钟，到一个离家1000米的图 书室，看了40分钟的书后，用20分钟返回到家，下图中表 示小颖离家时间与距离之间的关系的是（ ）,D,三检测,2.如果A、B两人在一次百米赛跑中，路程s（米）与赛 跑的时间t（秒）的关系如图所示，则下列说法正确的 是（ ） （A）A比B先出发 （B）A、B两人的速度相同 （C）A先到达终点 （D）B比A跑的路程多,C,3某装水的水池按一定的速度放掉水池中水的一半后， 停止放水并立即按一定的速度注水，水池注满后，停止注水，又立即按一定的速度放完水池的水.若水池的存水量为v（立方米），放水或注水的时间为t（分钟），则v与t的关系的大
12、致图象只能（ ）,A,4.如图，是张老师出门散步时离家的距离与时间之间的函数关系的图象，若用黑点表示张老师家的位置，则张老师散步行走的路线可能是 【解析】选.根据题中所给函数的图象和函数的意义易知张老师散步行走的路线可能是.,5.周末，小李8时骑自行车从家里出发，到野外郊游，16时回到家里他离开家后的距离S（千米）与时间t（时）的关系可以用图中的折线表示根据这个图象回答下列问题： (1)小李到达离家最远的地方是什么时间？,(2)小李何时第一次休息？,14时,10时,(3)10时到13时，小李骑了多少千米？,(4)返回时，小李的平均车速是多少？,25-20=5（千米）,30（16-14）=15（
13、千米/小时）,、（1）画出函数 的图象； 列表： 描点并连线：,AB不在，C在,（2）判断点A（-2.5，-4），B（1，3），C（2.5，4）是否在函数 的图象上,描点并连线： （2）从图象中观察，当x0时，y随x的增大而增大，还是y随x的增大而减小?,、（1）画出函数 的图象； 列表：,y随x的增大而减小,（1）函数图象上点的横坐标和纵坐标分别表示什么？ （2）画函数图象时，能画出满足函数关系的所有的吗？ （3）你认为观察函数图象时要注意哪些问题？,1.课堂小结,图象信息（形）,图象上点的坐标特点（数）,对应关系和变化规律,四 拓展,（4）怎样判断一个点是否在函数的图象上,.王教授和孙子小
14、强经常一起进行早锻炼，主要活动是爬山有一天，小强让爷爷先上，然后追赶爷爷图中两条线段分别表示小强和爷爷离开山脚的距离（米）与爬山所用时间（分）的关系（从小强开始爬山时计时）.,图中直角坐标系的横轴（x轴）和纵轴（y轴）各表示什么？,横轴（x轴）表示两人爬山所用时间；纵轴（y轴）表示两人离开山脚的距离,2.知识延伸,（1）小强让爷爷先上多少米？,小强出发0分钟时，爷爷已经爬山60米，因此小强让爷爷先上60米；,想一想,（2）山顶高多少米？谁先爬上山顶？,山顶离山脚的距离是300米，小强先爬上山；,（3）小强通过多少时间追上爷爷？,因为小强和爷爷路程相等时是8分钟，所以小强用了8分钟追上爷爷；,小强爬山300米用了10分钟，速度为30米分，爷爷爬山（300-60）米=240米，用了10.5分钟，速度约为23米分，因此小强的速度大，大7米分.,（4）谁的速度大，大多少？,
