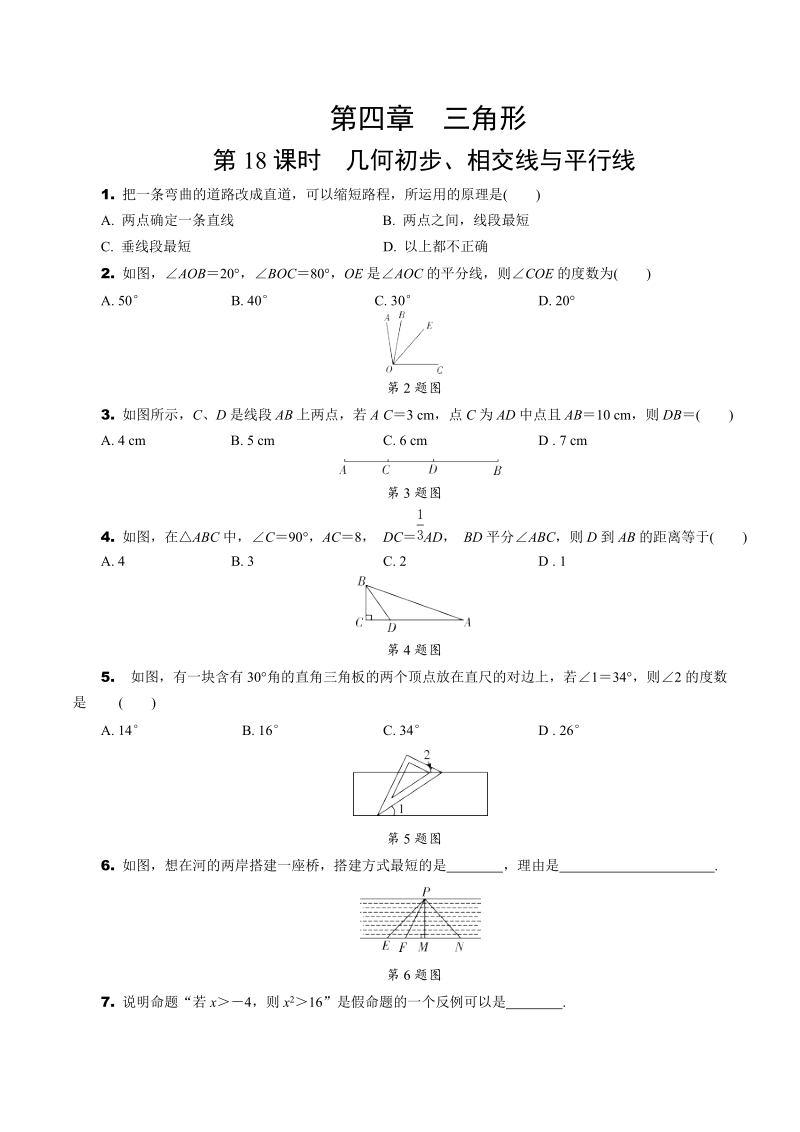
1、第四章三角形第18课时几何初步、相交线与平行线1. 把一条弯曲的道路改成直道，可以缩短路程，所运用的原理是()A. 两点确定一条直线 B. 两点之间，线段最短C. 垂线段最短 D. 以上都不正确2. 如图，AOB20，BOC80，OE是AOC的平分线，则COE的度数为()A. 50 B. 40 C. 30 D. 20第2题图3. 如图所示，C、D是线段AB上两点，若AC3 cm，点C为AD中点且AB10 cm，则DB()A. 4 cm B. 5 cm C. 6 cm D. 7 cm第3题图4. 如图，在ABC中，C90，AC8，DCAD， BD平分ABC，则D到AB的距离等于()A. 4 B.
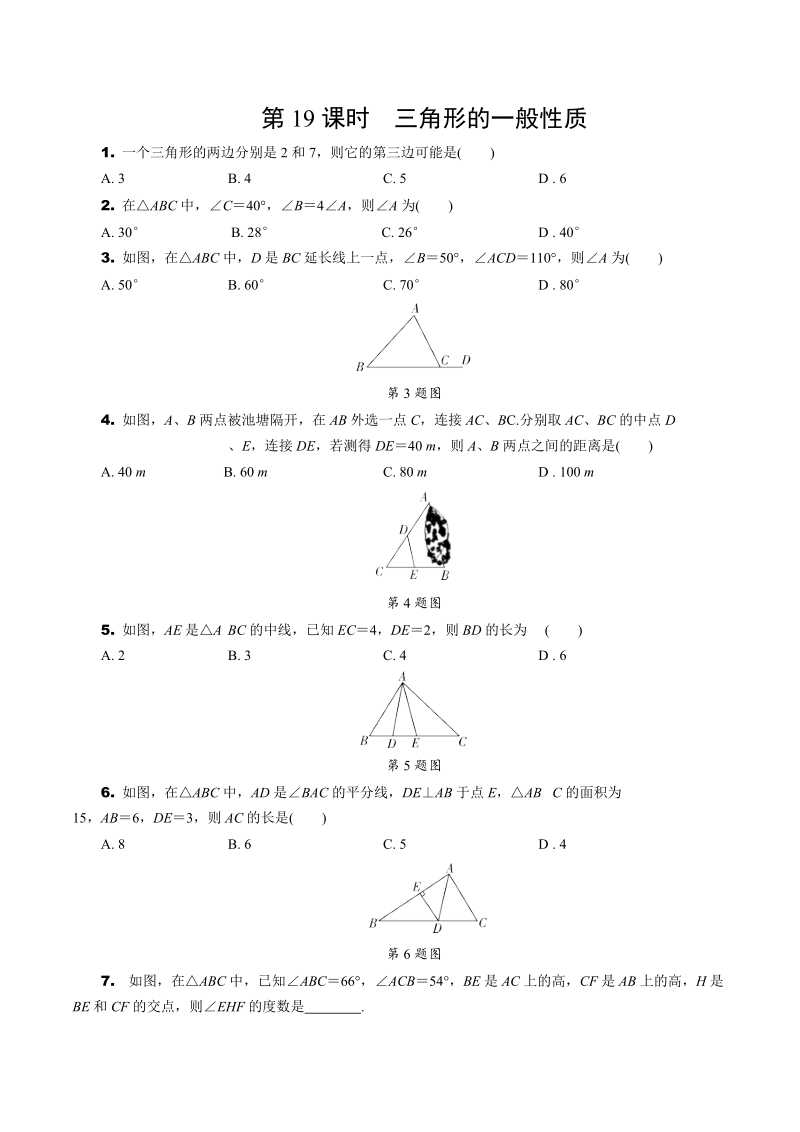
2、 3 C. 2 D. 1第4题图5. 如图，有一块含有30角的直角三角板的两个顶点放在直尺的对边上，若134，则2的度数是 ()A. 14 B. 16 C. 34 D. 26第5题图6. 如图，想在河的两岸搭建一座桥，搭建方式最短的是，理由是.第6题图7. 说明命题“若x4，则x216”是假命题的一个反例可以是.第19课时三角形的一般性质1. 一个三角形的两边分别是2和7，则它的第三边可能是()A. 3 B. 4 C. 5 D. 62. 在ABC中，C40，B4A，则A为()A. 30 B. 28 C. 26 D. 403. 如图，在ABC中，D是BC延长线上一点，B50，ACD110，则A为
3、()A. 50 B. 60 C. 70 D. 80第3题图4. 如图，A、B两点被池塘隔开，在AB外选一点C，连接AC、BC.分别取AC、BC的中点D、E，连接DE，若测得DE40 m，则A、B两点之间的距离是()A. 40 m B. 60 m C. 80 m D. 100 m第4题图5. 如图，AE是ABC的中线，已知EC4，DE2，则BD的长为 ()A. 2 B. 3 C. 4 D. 6第5题图6. 如图，在ABC中，AD是BAC的平分线，DEAB于点E，ABC的面积为15，AB6，DE3，则AC的长是()A. 8 B. 6 C. 5 D. 4第6题图7. 如图，在ABC中，已知ABC66
4、，ACB54，BE是AC上的高，CF是AB上的高，H是BE和CF的交点，则EHF的度数是.第20课时等腰三角形1. 已知等腰三角形顶角的度数是30，则底角的度数为()A. 60 B. 65 C. 70 D. 752. 若一个等腰三角形的两边长为4、9，则它的周长为()A. 17 B. 22 C. 17或22 D. 无法计算3. 如图，等边ABC的周长为18，则BC边上的高AD的长为()A. 3 B. 3 C. 6 D. 6第3题图4. 如图，在ABC中，ACADDB，C70，则CAB的度数为()A. 75 B. 70 C. 40 D. 35第4题图5. 下列说法：等边三角形的三个内角都相等；等
5、边三角形的每一个角都等于60；三个角都相等的三角形是等边三角形；有一个角是60的等腰三角形是等边三角形.其中，正确说法的个数是()A. 1 B. 2 C. 3 D. 46. 如图，在ABC中，已知BC，BDCD，则下列判断不一定正确的是()A. ABAC B. ADBCC. ABC为等边三角形 D. BADCAD第6题图7. 如图，BD，CE分别是ABC的高线和角平分线，且相交于点O.若ABAC，A40，则BOE的度数是()A. 60 B. 55 C. 50 D. 40第7题图8. 如图，在ABC中，ABAC，A30，AB的垂直平分线交AC于点E，垂足为点D，连接BE，则EBC的度数是()A.
6、 30 B. 45 C. 60 D. 75第8题图9. 如图，AD是等边ABC的中线，AEAD，则EDC的度数为()A. 30 B. 20 C. 25 D. 15第9题图10. 如图，在ABC中，CD是ACB的平分线，DEBC交AC于点E，若DE6，AE5，则AC.第10题图11. 已知：如图，在ABC中，12，DEAC，求证：AEDE.第11题图12. 已知：如图，在等边ABC的AC边上取中点D，BC的延长线上取一点E，使BDDE.求证：CDCE.第12题图第21课时直角三角形1. 下列各组数中，不是直角三角形的三条边的长的是 ()A. 3，4，5 B. 6，8，10 C. 5，12，13
7、D. 4，5，62. 若直角三角形中，有两边长是5和4，则第三边长为()A. 41 B. 3 C. 9或41 D. 3或3. 如图，ABC是等腰直角三角形，ABAC，BAC90，AD是底边BC上的高.BC10，则AD的长是()A. 5 B. 5 C. 8 D. 10第3题图4. 如图，在RtABC中，C90，A30，D是AC边的中点，DEAC于点D，交AB于点E，若AB16，则DE的长是()A. 8 B. 6 C. 4 D. 2第4题图5. 如图，在RtABC中，ACB90，B30，CD是斜边AB上的高，AD3 cm，则BD的长度是()A. 3 cm B. 6 cm C. 9 cm D. 12
8、 cm第5题图6. 如图，在RtABC中，ACB90，CD是AB边上的高，CE是AB边上的中线，AD3，CE5，则CD()A. 3 B. 4 C. D. 第6题图7. 如图，在RtABC中，B90，ACB60，DE是斜边AC的垂直平分线，分别交AB、AC于D、E两点，若BD2，则AC的长是()A. 4 B. 4 C. 8 D. 8第7题图8. 如图，ABC为等腰直角三角形，ABC90，ADB为等边三角形，则ADC.第8题图9. 如图，在RtABC中，ACB90，CD是AB边上的中线，DEAB于点D，交AC于点E.(1)若BC3，AC5，求CD的长；(2)求证：12第9题图第22课时解直角三角形
9、及其应用1. 如图，在RtABC中，C90，AB5，BC4，则下列表示正确的是()A. tanA B. tanB C. sinA D. cosA第1题图2. 已知是锐角，sincos60，则()A. 30 B. 45 C. 60 D. 不能确定3. 如图，在84的正方形网格中，若ABC的三个顶点在图中相应的格点上，则tanACB()A. B. C. D. 第3题图4. 如图，在平面直角坐标系中，点M的坐标为(，2)，则cos ()A. B. C. D. 第4题图5. 如图，在ABC中，ACB90，sinA，CD平分ACB，则BDC的度数是()第5题图A. 45 B. 60 C. 70 D. 7
10、56. 如图，已知ABC中，AB4，tanC，过点A作ADBC交边BC于点D，且ADBD，则BC()第6题图A. 8 B. 8 C. 7 D. 77. 如图，在RtACB中，BCA90，AC8，sinA，点D是AB中点，则CD的长为()A. 4 B. 5 C. 6 D. 7第7题图8. 如图，传送带和地面所成斜坡AB的坡角为30，物体沿传送带上升到点B时，距离地面的高度为3米，则斜坡AB的长度为()A. 3米 B. 5米 C. 4米 D. 6米第8题图9. 如图，某地修建高速公路，要从B地向C地修一座隧道(B，C在同一水平面上)，为了测量B，C两地之间的距离，某工程师乘坐热气球从C地出发，垂直
11、上升200米到达A处，在A处观察B地的俯角为，则B，C两地之间的距离为()A. 200sin米 B. 200tan米 C. 米 D. 米第9题图10. 如图，港口A在观测站O的正东方向，OA2 km，某船从港口A出发，沿北偏东15方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60的方向，则该船航行的距离(即AB的长)为()A. 2 km B. km C. km D. (1)km第23课时全等三角形1. 如果ABCDEF，DEF的周长为12，AB3，BC4，则AC的长为()A. 2 B. 3 C. 4 D. 52. 如图，已知ABC，点D，E在边BC上，ABDACE.下列结论不一
12、定成立的是()A. ABAC B. BDCE C. CACD D. BAECAD第2题图3. 如图，有一池塘，要测池塘两端A，B间的距离，可先在平地上取一个不经过池塘可以直接到达点A和B的点C，连接AC并延长至点D，使CDCA，连接BC并延长至点E，使CECB，连接ED.若量出DE58米，则A，B间的距离即可求得.依据是()A. SAS B. SSS C. AAS D. ASA4. 如图，已知AC，BD相交于点O，ADBC，ACBD，求证：OAOB.第4题图5. 如图，四边形ABCD中，D90，ABAC，BEAC于点E，AEAD.求证：AC平分DAB.第5题图6. 如图，BCA90，ACBC，
13、BECF于点E，AFCF于点F，其中0ACF45.求证：BECCFA.第6题图7. 如图，点E、F在AC上，DFBE，AECF，AFDCEB.求证：ADCB.第7题图8. 如图，AB，AEBE，点D在AC边上，12.求证：EDCC.第8题图第24课时尺规作图1. 如图，用直尺和圆规作一个角等于已知角，那么能得出AOBAOB的依据是运用了我们学习的全等三角形判定()第1题图A. AAS B. SAS C. ASA D. SSS2. 如图，是作线段AB的垂直平分线的尺规作图，其中没有用到的依据是()A. 同圆或等圆的半径相等B. 两点之间线段最短C. 到线段两端距离相等的点在线段的垂直平分线上D.
14、 两点确定一条直线第2题图3. 如图，一位同学用直尺和圆规作出了ABC中BC边上的高AD，则一定有()A. PAPC B. PAPQ C. PQPC D. QPC90第3题图4. 如图在RtABC中，C90，以顶点A为圆心，适当长为半径画弧，分别交AC、AB于点M、N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交BC于点D，若CD2，AB8，则ABD的面积是()A. 16 B. 32 C. 8 D. 4 第4题图 第5题图5. 如图，在ABC中，C50，B35，分别以点A，B为圆心，大于AB的长为半径画弧，两弧相交于点M，N，直线MN交BC于点D，连接AD.则DA
15、C的度数为()A. 85 B. 70 C. 60 D. 256. 下面是小松设计的“做圆的内接等腰直角三角形”的尺规作图过程.已知：O.求作：O的内接等腰直角三角形.作法：如图，作直径AB；第6题图分别以点A，B为圆心，以大于AB的同样长为半径作弧，两弧交于M，N两点；作直线MN交O于点C，D；连接AC，BC.所以ABC就是所求作的三角形.根据小松设计的尺规作图过程：(1)使用直尺和圆规，补全图形；(保留作图痕迹)(2)完成下面的证明.证明：AB是直径，C是O上一点.ACB90(填写推理依据).ACBC(填写推理依据)，ABC是等腰直角三角形.第25课时图形的相似(含位似)1. 由5a6b(a
16、0)，可得比例式()A. B. C. D. 2. 两个相似多边形的相似比是23，则这两个多边形的周长比是()A. 49 B. C. 25 D. 233. 已知ABCDEF，若面积比为49，则它们对应高的比是()A. 49 B. 1681 C. 35 D. 234. 如图，ABCDEF，AC4，CE6，BD3，则DF()A. 4.5 B. 5 C. 2 D. 1.5第4题图5. 如图，在平面直角坐标系中，已知点A(2，4)，过点A作ABx轴于点B.将AOB以坐标原点O为位似中心缩小为原图形的，得到COD，则CD的长度是()第5题图A. 1 B. 2 C. 2 D. 6. 如图，已知AB，CD相交
17、于点O，ACBD，CO6，则DO()A. 21 B. 15 C. 9 D. 5第6题图7. 如图，在ABC中，DEBC，ADDB23，则SADESEBC()第7题图A. 415 B. 23 C. 49 D. 4258. 如图，在ABC中，DEBC，则下列结论正确的是()A. B. C. D. 第8题图9. 如图，在ABC中，点D，E分别在边AB、AC上，下列条件中不能判断ADEACB的是()第9题图A. AEDABC B. ADECC. D. 10. 如图，小颖为测量学校旗杆AB的高度，她在E处放置一块镜子，然后退到C处站立，刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD1.5
18、 m，她离镜子的水平距离CE0.5 m，镜子E离旗杆的底部A处的距离AE2 m，且A、C、E三点在同一水平直线上，则旗杆AB的高度为()A. 4.5 m B. 4.8 m C. 5.5 m D. 6 m第10题图11. 如图，以点O为位似中心，将四边形ABCD按12放大得到四边形ABCD，则四边形ABCD与四边形ABCD的面积比是.第11题图12. 如图，在ABC中，AB4，AC3，D是AB边上的一点.若ABCACD，AD的长为.第12题图 参考答案第四章三角形第18课时几何初步、相交线与平行线1. B2. A【解析】AOB20，BOC80，AOCAOBBOC100.OE是AOC的平分线，CO
19、EAOC50.3. A【解析】点C为AD的中点，AC3 cm，CD3 cm.AB10 cm，ACCDDBAB，BD10334 cm.4. C【解析】如解图，过点D作DEAB于点E，DCAD，DCAC.AC8，DC82.C90，BCCD.又BD平分ABC，DEDC2，故选C.第4题解图5. D【解析】如解图，ABC60，134，BECD，EBC34.2ABCEBC26.第5题解图6. PM，直线外一点与直线上各点连接的所有线段中，垂线段最短7. x3【解析】说明命题“若x4，则x216”是假命题的一个反例可以是x3.答案不唯一第19课时三角形的一般性质1. D【解析】设第三边为a，根据三角形的三
20、边关系可得72a72.即5a9，故选D.2. B【解析】ABC180，5A40180.A28.3. B【解析】ACD110，ACB18011070，B50，A180ACBB60.4. C【解析】D、E分别是AC、BC的中点，AB2DE80(m).5. A【解析】AE是ABC的中线，EC4，BEEC4.DE2，BDBEDE422.6. D【解析】如解图，过点D作DFAC于点F，AD是BAC的平分线，DEAB，DEDF3.SABC63AC315，解得AC4.第6题解图7. 120【解析】ABC66，ACB54，A60.CF是AB上的高，在ACF中，ACF180AFCA30，在CEH中，ACF30，
21、CEH90.EHFACFCEH3090120.第20课时等腰三角形1. D【解析】等腰三角形两底角相等，若顶角度数为30，则底角度数75.2. B【解析】若4为腰长，9为底边长，449，该三角形不存在；若9为腰长，则符合三角形三边关系的性质这个三角形的周长为99422.3. B【解析】等边ABC周长为18，ABBCCA6，BDBC3.在RtABD中，AD3.4. A【解析】ACADDB，CADC70，BDAB.CAD180707040.ADCBDAB，DABB35.CABCADDAB75.5. D6. C【解析】BC，ABAC.BDCD，ADBC.BADCAD.故A、B、D正确，C错误7. B
22、【解析】ABAC，A40，ABCACB(18040)70.CE平分ACB，ACEACB35.BDAC，ODC90.BOECOD903555.8. B【解析】DE垂直平分AB，EAEB.ABEA30.ABAC，ABCC.ABC(18030)75.EBCABCABE753045.9. D【解析】AD是等边ABC的中线，ADBC，BADCADBAC6030.ADC90.ADAE，ADEAED(180CAD)75.EDCADCADE907515.10. 11【解析】CD平分ACB交AB于点D，ACDDCB.DEBC，EDCDCB.EDCECD.DEEC6.AE5，ACAEEC5611.11. 证明：D
23、EAC，ADE2.12，ADE1.AEDE.12. 证明：ABC是等边三角形，ABCACB60.ADDC，DBCABC30.DBDE，EDBC30.ACBCDEEEDC30.EEDC.CDCE.第21课时直角三角形1. D【解析】A.324252，B.6282102，C.52122132.均能构成直角三角形，D.425262.故选D.2. D【解析】当5是直角边时，斜边，当5是斜边时，另一条直角边3，则第三边长为3或.3. A【解析】ABC是等腰直角三角形，BAC90，BC(180BAC)45.AD是底边BC上的高，ADB90，DABB45.ADBDBC5.4. C【解析】在RtABC中，C9
24、0，A30，AB16，BCAB8.DEAC，C90，DEBC.D是AC边的中点，ADCD.AEBE.DEBC4.5. C【解析】在RtABC中，CD是斜边AB上的高，ADC90.ACDB30(同角的余角相等).AD3 cm，在RtACD中，AC2AD6 cm，在RtABC中，AB2AC12 cm，BDABAD1239 cm.6. C【解析】在RtABC中，ACB90，CE为AB边上的中线，CE5.AECE5.AD3，DE2.CD为AB边上的高，在RtCDE中，CD.7. B【解析】B90，ACB60，A30.DE是斜边AC的垂直平分线，DADC.DCAA30，DCB30.DC2BD4.由勾股定
25、理得BC2，AC2BC4.8. 135【解析】ABD是等边三角形，ABDADB60，BABD.BABC，ABC90，BDBC，CBD30，BDCBCD(18030)75.ADCADBBDC135.9. (1)解：ACB90，AB.CD是AB边上的中线，CDAB；(2)证明：DCDB，AB90.B2.A290.DEAB，A190.12.第22课时解直角三角形及其应用1. D【解析】A.tan A，B.tan B，C.sin A，A、B、C错误，故选D.2. A3. A【解析】如解图，在正方形网格中，过点A作ADCB的延长线于点D，连接BD.则AD2，CD6.在RtACD中，tan ACB.第3题
26、解图4. D【解析】如解图，过点M作MAx轴于点A，由点M的坐标可得：MA2，OA，OM3，则cos .第4题解图5. D【解析】在ABC中，ACB90，sin A，CD平分ACB，A30，ACD45.BDCAACD，BDC304575.6. C【解析】ADBC，ADBADC90.AB4，BDAD，ADBD4.tan C，CD3.BCBDCD437.7. B【解析】设BC3x，则AB5x，AC4x，4x8.x2.AB5x10.在RtACB中，AB10，点D是AB中点，CDAB5.8. D【解析】如解图，过点B作BC地面于点C，在RtABC中，A30，BC3 米，sin A.即，AB6米第8题解
27、图9. D【解析】根据题意得：ABC，ACBC，AC200米，在RtABC中，BC(米).10. C【解析】如解图，过点A作ADOB于点D.在RtAOD中，ADO90，AOD30，OA2，ADOA1.在RtABD中，ADB90，BCABAOB753045，BDAB45，BDAD1.ABAD.即该船航行的距离(即AB的长)为 km.第10题解图第23课时全等三角形1. D【解析】ABCDEF，DEF的周长为12，ABC的周长为12.又AB3，BC4，AC5.2. C【解析】ABDACE，ABAC，BDCE，BADCAE.BAEBADDAE，CADCAEDAE，BAECAD.故A、B、D正确，C错
28、误3. A4. 证明：在ABC与BAD中，ABCBAD(SSS).ABDBAC.OAOB.5. 证明：BEAC，AEBD90.在RtADC与RtAEB中，RtADCRtAEB(HL).DACBAC，AC平分DAB.6. 证明：BECF，BCA90，BBCE90，BCEACF90.BACF，且ACBC，BECAFC90.BECCFA(AAS).7. 证明：AECF，AEEFCFEF，即AFCE.又AFDCEB，DFBE，ADFCBE(SAS).AC.ADCB.8. 证明：ADE1C2BDE，且12，CBDE.且AB，AEBE.BDEACE(AAS).DEEC.EDCC.第24课时尺规作图1. D
29、2. B【解析】作线段AB的垂直平分线的尺规作图，其中用到的依据有：同圆或等圆的半径相等；到线段两端距离相等的点在线段的垂直平分线上；两点确定一条直线3. C【解析】如解图，连接PQ，PC，由题意可知该尺规作图的步骤为过直线BC外一点A作BC的垂线，易知AD为QC的垂直平分线PQPC.第3题解图4. C【解析】如解图，过点D作DHAB于点H.由作图可知：PA平分CAB，DCAC，DHAB，DHDC2.SABDABDH828.第4题解图5. C【解析】在ABC中，B35，C50，BAC180BC95.由作图可知MN为AB的中垂线，DADB.DABB35.CADBACDAB60.6. 解：(1)补
30、全的图形如解图所示：第6题解图(2)直径所对的圆周角是直角；线段垂直平分线上的点到线段两个端点的距离相等第25课时图形的相似(含位似)1. A2. D【解析】由相似多边形的周长比等于相似比可知选项D正确3. D【解析】相似三角形的面积比等于相似比的平方，则选项D正确4. A【解析】直线ABCDEF，AC4，CE6，BD3，即，解得DF4.5.5. B【解析】由题意可得：CDAB2.6. B【解析】ACBD，CD，AB.AOCBOD.，CO6，DO15.7. A【解析】DEBC，ADDB23，ADEABC.SADESABC()2，SADESABC.SBECSABC，SBECSABC.SADESEBC415.8. C【解析】在ABC中，DEBC，ADEABC.，A错误；，B错误；，C正确；()2.D错误9. C【解析】A.ABCAED，AA，则可判断ADEACB，故A选项错误；B.ADEC，AA，则可判断ADEACB，故B选项错误；C.，不能判定ADEACB，故C选项正确；D.，且夹角AA，能确定ADEACB，故D选项错误10. D【解析】由题意可得AE2 m，CE0.5 m，DC1.5 m，EBAEDC，即，解得AB6 m.11. 14【解析】面积比等于相似比的平方，相似比为12，则面积比为14.12. 【解析】ABCACD，AB4，AC3，AD.
