1、2.2分层抽样与系统抽样学习目标1.理解并掌握系统抽样、分层抽样.2.会用系统抽样、分层抽样从总体中抽取样本.3.理解三种抽样的区别与联系.知识点一分层抽样1.分层抽样的概念将总体按其属性特征分成若干类型(有时称作层)，然后在每个类型中按照所占比例随机抽取一定的样本.这种抽样方法通常叫作分层抽样，有时也称为类型抽样.2.分层抽样的适用条件分层抽样尽量利用事先所掌握的各种信息，并充分考虑保持样本结构与总体结构的一致性，这对提高样本的代表性非常重要.当总体是由差异明显的几个部分组成时，往往选用分层抽样的方法.3.分层抽样的实施步骤第一步，按某种特征将总体分成若干部分(层)；第二步，计算抽样比.抽样
2、比；第三步，各层抽取的个体数各层总的个体数抽样比；第四步，依各层抽取的个体数，按简单随机抽样从各层抽取样本；第五步，综合每层抽样，组成样本.思考分层抽样的总体具有什么特性？答案分层抽样的总体由差异明显的几部分构成，也就是说当已知总体由差异明显的几部分组成时，为了使样本充分地反映总体的情况，常将总体分成几部分，然后按照各部分所占的比例进行抽样.知识点二系统抽样1.系统抽样的概念将总体中的个体进行编号，等距分组，在第一组中按照简单随机抽样抽取第一个样本，然后按分组的间隔(称为抽样距)抽取其他样本.这种抽样方法有时也叫等距抽样或机械抽样.2.系统抽样的步骤假设要从容量为N的总体中抽取容量为n的样本，
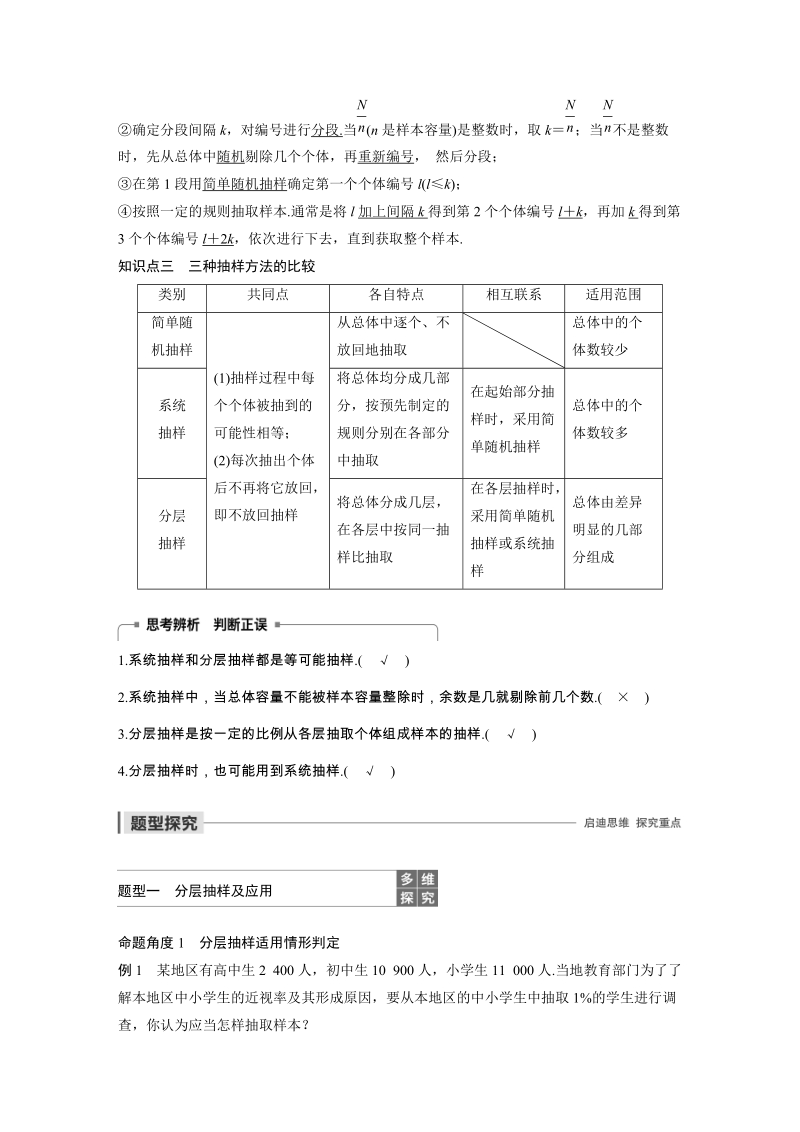
3、步骤为：先将总体的N个个体编号.有时可直接利用个体自身所带的号码，如学号、准考证号、门牌号等；确定分段间隔k，对编号进行分段.当(n是样本容量)是整数时，取k；当不是整数时，先从总体中随机剔除几个个体，再重新编号， 然后分段；在第1段用简单随机抽样确定第一个个体编号l(lk)；按照一定的规则抽取样本.通常是将l加上间隔k得到第2个个体编号lk，再加k得到第3个个体编号l2k，依次进行下去，直到获取整个样本.知识点三三种抽样方法的比较类别共同点各自特点相互联系适用范围简单随机抽样(1)抽样过程中每个个体被抽到的可能性相等；(2)每次抽出个体后不再将它放回，即不放回抽样从总体中逐个、不放回地抽取总
4、体中的个体数较少系统抽样将总体均分成几部分，按预先制定的规则分别在各部分中抽取在起始部分抽样时，采用简单随机抽样总体中的个体数较多分层抽样将总体分成几层，在各层中按同一抽样比抽取在各层抽样时，采用简单随机抽样或系统抽样总体由差异明显的几部分组成1.系统抽样和分层抽样都是等可能抽样.()2.系统抽样中，当总体容量不能被样本容量整除时，余数是几就剔除前几个数.()3.分层抽样是按一定的比例从各层抽取个体组成样本的抽样.()4.分层抽样时，也可能用到系统抽样.()题型一分层抽样及应用命题角度1分层抽样适用情形判定例1某地区有高中生2 400人，初中生10 900人，小学生11 000人.当地教育部门
5、为了了解本地区中小学生的近视率及其形成原因，要从本地区的中小学生中抽取1%的学生进行调查，你认为应当怎样抽取样本？解(1)从总体来看，因为不同年龄阶段的学生的近视情况可能存在明显差异，为了使样本具有较好的代表性，应该分高中、初中、小学三个层次分别抽样.(2)从三类学生的数量来看，人数较多，所以在各层抽样时可以采用系统抽样.(3)采用系统抽样分好组之后，确定第一组人选时，可以采用简单随机抽样.反思感悟分层抽样实质是利用已知信息尽量使样本结构与总体结构相似.在实际操作时，并不排斥与其他抽样方法联合使用.跟踪训练1为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了
6、解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大，则在下面的抽样方法中，最合理的抽样方法是()A.简单随机抽样 B.按性别分层抽样C.按学段分层抽样 D.系统抽样答案C解析当总体由差异明显的几部分组成时，按属性特征分层，所以应按学段分层抽样.命题角度2分层抽样具体实施步骤例2某学校有在职人员160人，其中行政人员有16人，教师有112人，后勤人员有32人.教育部门为了了解在职人员对学校机构改革的意见，要从中抽取一个容量为20的样本，请利用分层抽样的方法抽取，写出抽样过程.解抽样过程如下：第一步，确定抽样比，样本容量与总体容量的比为.第二步，确定分别从三类人员
7、中抽取的人数，从行政人员中抽取162(人)；从教师中抽取11214(人)；从后勤人员中抽取324(人).第三步，采用简单随机抽样的方法，抽取行政人员2人，教师14人，后勤人员4人.第四步，把抽取的个体组合在一起构成所需样本.反思感悟在分层抽样的过程中，为了保证每个个体被抽到的可能性是相同的，这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体容量之比.跟踪训练2某市的3个区共有高中学生20 000人，且3个区的高中学生人数之比为235，现要从所有学生中抽取一个容量为200的样本，调查该市高中学生的视力情况，试写出抽样过程.解(1)由于该市高中学生的视力有差异，按3个区分成三层，
8、用分层抽样法抽取样本.(2)确定每层抽取个体的人数，在3个区分别抽取的学生人数之比也是235，所以抽取的学生人数分别是20040；20060；200100.(3)在各层分别按系统抽样法抽取样本.(4)综合每层抽样，组成容量为200的样本.题型二系统抽样及应用例3为了了解参加某种知识竞赛的1 000名学生的成绩，从中抽取一个容量为50的样本，那么采用什么抽样方法比较恰当？简述抽样过程.解适宜选用系统抽样，抽样过程如下：(1)随机地将这1 000名学生编号为1,2,3，1000.(2)将总体按编号顺序均分成50个部分，每部分包括20个个体.(3)在第一部分的个体编号1,2,3，20中，利用简单随机
9、抽样抽取一个号码l.(4)以l为起始号码，每间隔20抽取一个号码，这样得到一个容量为50的样本：l，l20，l40，l980.引申探究在本例中，如果总体是1 002，其余条件不变，又该怎么抽样？解(1)将每个学生编一个号，由1至1 002.(2)利用随机数法剔除2个号.(3)将剩余的1 000名学生重新编号1至1 000.(4)按编号顺序均分成50个部分，每部分包括20个个体.(5)在第一部分的个体编号1,2,3，20中，利用简单随机抽样抽取一个号码l.(6)以l为起始号码，每间隔20抽取一个号码，这样得到一个容量为50的样本：l，l20，l40，l980.反思感悟当总体中的个体数不能被样本容
10、量整除时，需要在总体中剔除一些个体.由于剔除方法采用简单随机抽样，所以即使是被剔除的个体，在整个抽样过程中被抽到的机会和其他个体是一样的.跟踪训练3某工厂有1 003名工人，从中抽取10人参加体检，试用系统抽样进行具体实施.解(1)将每个工人编一个号，由1至1 003.(2)利用随机数法找到3个号将这3名工人剔除.(3)将剩余的1 000名工人重新编号1至1 000.(4)分段，取间隔k100，将总体均分为10组，每组100个工人.(5)从第一段即1号到100号中随机抽取一个号l.(6)按编号将l,100l,200l，900l，共10个号选出.这10个号所对应的工人组成样本.分层抽样时各层样本
11、数的确定典例一个单位有职工500人，其中不到35岁的有125人，35岁至50岁的有280人，50岁以上的有95人.为了了解这个单位职工与身体状态有关的某项指标，要从中抽取100名职工作为样本，职工年龄与这项指标有关，请分层并确定各层抽取人数.解(1)分层.按年龄将500名职工分成三层：不到35岁的职工；35岁至50岁的职工；50岁以上的职工.(2)确定每层抽取个体的个数.抽样比为，则在不到35岁的职工中抽取12525(人)；在35岁至50岁的职工中抽取28056(人)；在50岁以上的职工中抽取9519(人).引申探究把本题中的“其中不到35岁的有125人，35岁至50岁的有280人，50岁以上
12、的有95人”改为“不到35岁的人数、35岁至50岁的人数、50岁以上的人数的比为532”，其他条件不变，应怎样抽取？解用分层抽样来抽取样本，步骤是：(1)分层：按年龄将500名职工分成三层，各层人数：不到35岁的职工500250(人)；35岁至50岁的职工500150(人)；50岁以上的职工500100(人).(2)确定每层抽取个体的个数，抽样比为，则在不到35岁的职工中抽取25050(人)；在35岁至50岁的职工中抽取15030(人)；在50岁以上的职工中抽取10020(人).素养评析(1)分层抽样的关键：一是将总体按一定属性特征进行分层；二是计算各层抽取的样本数.(2)按照等比例的原则，进
13、行计算，体现了运算方法，运算法则的应用，充分体现了数学运算的核心素养.1.某校高三年级有男生500人，女生400人，为了解该年级学生的健康状况，从男生中任意抽取25人，从女生中任意抽取20人进行调查.这种抽样方法是()A.简单随机抽样 B.抽签法C.随机数法 D.分层抽样答案D解析从男生500人中抽取25人，从女生400人中抽取20人，抽取的比例相同，因此用的是分层抽样.2.检测员每10分钟从匀速传递的新产品生产流水线上抽取一件新产品进行某项指标检测，这样的抽样方法是()A.系统抽样法 B.抽签法C.随机数法 D.其他抽样方法答案A解析根据系统抽样的定义和性质进行判断即可.3.为了解1 200
14、名学生对学校食堂饭菜的意见，打算从中抽取一个样本容量为40的样本，考虑采用系统抽样，则分段间隔k为()A.10 B.20C.30 D.40答案C解析分段间隔k30.4.为了调查某省各城市PM2.5的值，按地域把36个城市分成甲、乙、丙三组，对应的城市数分别为6,12,18.若用分层抽样的方法抽取12个城市，则乙组中应抽取的城市数为_.答案4解析乙组城市数占总城市数的比例为，样本容量为12，故乙组中应抽取的城市数为124.5.某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查，已知该校一年级、二年级、三年级、四年级的本科生人数之比为4556，则应从一年级本科生中抽取_名学生.答案60解析根据题意，应从一年级本科生中抽取的人数为30060.1.系统抽样有以下特点：(1)适用于总体容量较大的情况；(2)剔除多余个体及第一段抽样都要用简单随机抽样，因而与简单随机抽样有密切联系；(3)是等可能抽样，每个个体被抽到的可能性都是；(4)是不放回抽样.在抽样时，只要第一段抽取的个体确定了，后面各段中要抽取的个体依照事先确定好的规律就自动地被抽出，因此简单易行.2.总体容量小，用简单随机抽样；总体容量大，用系统抽样；总体差异明显，用分层抽样.在实际抽样中，为了使样本具有代表性，通常要同时使用几种抽样方法.
