1、7.2棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积7.3球的表面积和体积基础过关1.某三棱锥的三视图如图所示，则该三棱锥的体积是()A. B. C. D.1解析如图，三棱锥的底面是一个直角边长为1的等腰直角三角形，有一条侧棱和底面垂直，且其长度为2，故三棱锥的高为2，故其体积V112，故选B.答案B2.已知长方体的过一个顶点的三条棱长的比是123，对角线的长是2，则这个长方体的体积是()A.6 B.12 C.24 D.48解析设长方体的过一个顶点的三条棱长分别为x、2x、3x(x0)，又对角线长为2，则x2(2x)2(3x)2(2)2，解得x2，三条棱长分别为2、4、6，V长方体24648.答案D
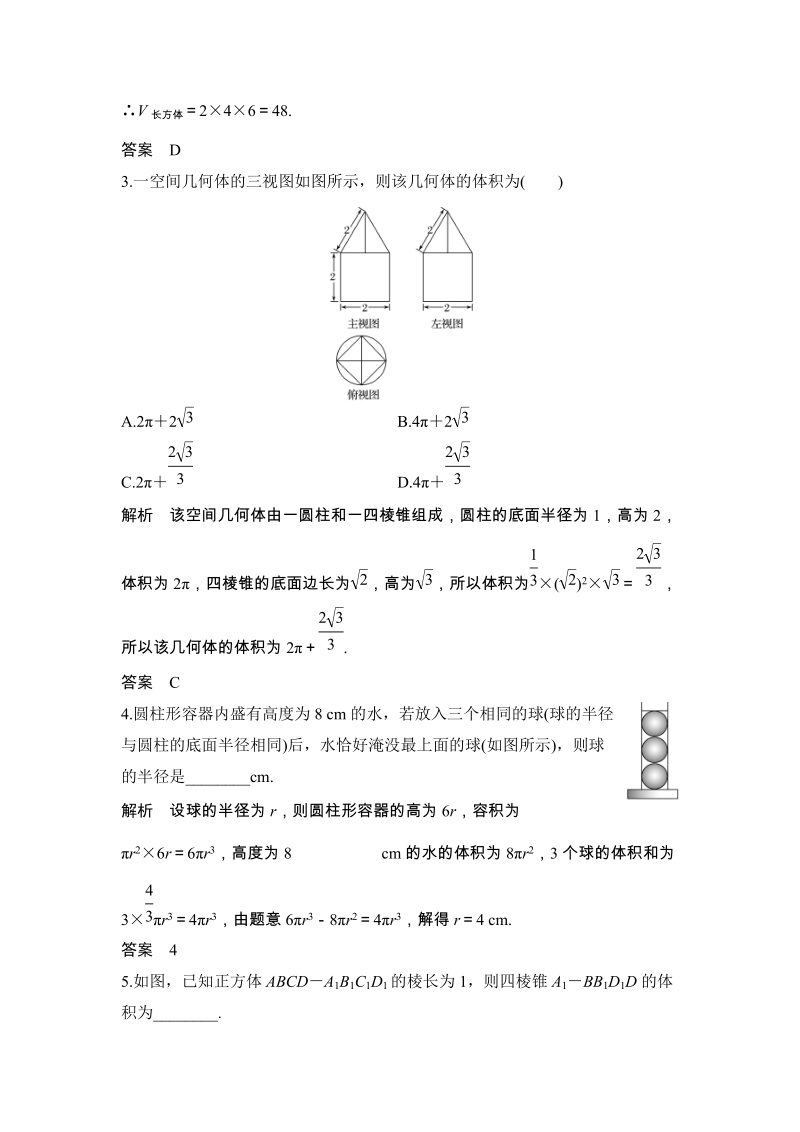
2、3.一空间几何体的三视图如图所示，则该几何体的体积为()A.22 B.42C.2 D.4解析该空间几何体由一圆柱和一四棱锥组成，圆柱的底面半径为1，高为2，体积为2，四棱锥的底面边长为，高为，所以体积为()2，所以该几何体的体积为2.答案C4.圆柱形容器内盛有高度为8 cm的水，若放入三个相同的球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的球(如图所示)，则球的半径是_cm.解析设球的半径为r，则圆柱形容器的高为6r，容积为r26r6r3，高度为8 cm的水的体积为8r2，3个球的体积和为3r34r3，由题意6r38r24r3，解得r4 cm.答案45.如图，已知正方体ABCDA1B
3、1C1D1的棱长为1，则四棱锥A1BB1D1D的体积为_.解析法一连接A1C1交B1D1于点E，则A1EB1D1，A1EBB1，则A1E平面BB1D1D，所以A1E为四棱锥A1BB1D1D的高，且A1E，矩形BB1D1D的长和宽分别为，1，故VA1BB1D1D1.法二连接BD1，则四棱锥A1BB1D1D分成两个三棱锥BA1DD1与BA1B1D1，VA1BB1D1DVBA1DD1VBA1B1D1111111.答案6.如图，在棱长为a的正方体ABCDA1B1C1D1中，求A到平面A1BD的距离d.解在三棱锥A1ABD中，AA1平面ABD，ABADAA1a，A1BBDA1Da，VA1ABDVAA1B
4、D，a2aaad.da.7.已知底面半径为 cm，母线长为 cm的圆柱，挖去一个以圆柱上底面圆心为顶点，下底面为底面的圆锥，求所得几何体的表面积及体积.解作轴截面如图，设挖去的圆锥的母线长为l，底面半径为r，则l3(cm)，r (cm).故几何体的表面积为Srlr22rAD3()22336(336)(cm2).几何体的体积为VV圆柱V圆锥r2ADr2AD332(cm3).能力提升8.已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为()A. B. C. D.解析如图画出圆柱的轴截面ABCD，O为球心.球半径ROA1，球心到底面圆的距离为OM.底面圆半径r，故圆柱
5、体积Vr2h1.答案B9.如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器厚度，则球的体积为()A. cm3 B. cm3C. cm3 D. cm3解析作出该球的轴截面图如图所示，依题意BE2，AECE4，设DEx，故AD2x，因为AD2AE2DE2，解得x3，故该球的半径AD5，所以VR3(cm3).答案A10.如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为_.解析正方体的棱长为2，以其所有面的中心为顶点的多面体是正八面体，其中正八面体的所有棱长都是，则该正八面体的体积为(
6、)22.答案11.已知三棱锥ABCD的所有棱长都为，则该三棱锥的外接球的表面积为_.解析如图，构造正方体ANDMFBEC.因为三棱锥ABCD的所有棱长都为，所以正方体ANDMFBEC的棱长为1.所以该正方体的外接球的半径为.易知三棱锥ABCD的外接球就是正方体ANDMFBEC的外接球，所以三棱锥ABCD的外接球的半径为.所以三棱锥ABCD的外接球的表面积为S球43.答案312.已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半，且AB18，BC24，AC30，求球的表面积和体积.解ABBCAC182430345，ABC是直角三角形，B90.球心O到截面ABC的投影O为截面圆的圆心，也
7、即是RtABC的外接圆的圆心，斜边AC为截面圆O的直径(如图所示).设OCr，OCR，则球半径R，截面圆半径r，在RtOCO中，由题设知sinOCO，OCO30，cos 30，即Rr，又2rAC30r15，代入得R10.球的表面积为S4R24(10)21 200.球的体积为VR3(10)34 000.创新突破13.有一个倒圆锥形容器，它的轴截面是一个正三角形，在容器内放一个半径为r的铁球，并注入水，使水面与球正好相切，然后将球取出，求这时容器中水的深度.解由题意知圆锥的轴截面为正三角形，如图所示为圆锥的轴截面.根据切线性质知，当球在容器内时，水深为3r，水面的半径为r，则容器内水的体积为VV圆锥V球(r)23rr3r3，而将球取出后，设容器内水的深度为h，则水面圆的半径为h，从而容器内水的体积是V(h)2hh3，由VV，得hr.即容器中水的深度为r.
