1、2018-2019学年广东省汕头市潮阳区高二（上）期末数学试卷（理科）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项符合题目要求.1（5分）已知集合Ax|x2k1，kz，Bx|x2x60，则AB（）A1，1B3，1，1C0，1，2D1，0，1，22（5分）一路口的红绿灯，红灯的时间为30秒，黄灯的时间为5秒，绿灯的时间为40秒当你到达此路口时，看见的不是绿灯的概率为（）ABCD3（5分）已知命题p：x1，x2R，（f（x1）f（x2）（x1x2）0，则p是（）Ax1，x2R，（f（x1）f（x2）（x1x2）0Bx1，x2R，（f（x1）f（x2）（
2、x1x2）0Cx1，x2R，（f（x1）f（x2）（x1x2）0Dx1，x2R，（f（x1）f（x2）（x1x2）04（5分）小吴一星期的总开支分布如图1所示，一星期的食品开支如图2所示，则小吴一星期的鸡蛋开支占总开支的百分比为（）A1%B2%C3%D5%5（5分）下列函数为奇函数的是（）Af（x）x3+3x2Bf（x）2x+2xCf（x）xsinxDf（x）ln6（5分）函数f（x）sinxcosx在下列哪个区间上是单调递减的（）A，0B0，CD7（5分）某程序框图如图所示，该程序运行后输出的k的值是（）A4B5C6D78（5分）“a”是“ln（2a1）0”成立的（）A充分不必要条件B充要条
3、件C必要不充分条件D既不充分也不必要条件9（5分）已知点M（3，8）在双曲线C：1（a0，b0）上，C的焦距为6，则它的离心率为（）A2B3C4D510（5分）已知实数x，y满足，则zx+的最大值为（）A7B1C10D011（5分）如图，四棱锥PABCD的底面ABCD是梯形，ABCD，若平面PAD平面PBCl，则（）AlCDBlBCCl与直线AB相交Dl与直线DA相交12（5分）若曲线与直线ykx1有两个不同的交点，则实数k的取值范围是（）ABCD二、填空题：本大题共4小题，每小题5分，共20分13（5分）已知地球表面及约是火星表面积的4倍，则地球体积是火星体积的 14（5分）已
4、知向量，间的夹角为，若（2，3），|，则 15（5分）九章算术中，将底面是直角三角形的直三棱柱称之为“堑堵”已知某“堑堵“的三视图如图所示，俯视图中间的实线平分矩形的面积，则该“堑堵”的表面积为 16（5分）已知抛物线y24x的焦点为F，点A（5，3），M为抛物线上一点且M不在直线AF上，则MAF周长的最小值为 三、解答题：本大题共70分，解答应写出文字说明、证明过程或演算步骤17（10分）已知在ABC中，角A，B，C所对的边分别为且a，b，c，且（1）求角A的大小；（2）若a6，sinB2sinC，求ABC的面积18（12分）已知圆的方程为：（x1）
5、2+y21求：（1）斜率为3且与圆相切直线的方程；（2）过定点（2，3）且圆相切的直线的方程19（12分）已知正项的等比数列an的前n项和为Sn，且（1）求数列an的通项公式；（2）若bnlog2an+3，数列的前n项和为Tn，求满足的正整数n的最小值20（12分）如图，四边形PDCE为矩形，四边形ABCD为梯形，平面PDCE平面ABCD，BADADC90，ABADCDa，PDa，M为PA中点（1）求证：AC平面MDE；（2）求直线ME与平面PBC所成角的正弦值21（12分）设函数f（x）（1）当a2时，求f（x）的单调区间；（2）当a0时，求不等式f（x）0的解集22（12分）已知椭圆+1（
6、ab0）的左、右焦点分别为F1，F2，离心率e，点P是椭圆上的一个动点，PF1F2面积的最大值是4（1）求椭圆的方程；（2）若A，B，C，D是椭圆上不重合的四点，AC与BD相交于点F1，且AC与BD垂直，又|AC|+|BD|，求此时直线AC的方程2018-2019学年广东省汕头市潮阳区高二（上）期末数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项符合题目要求.1（5分）已知集合Ax|x2k1，kz，Bx|x2x60，则AB（）A1，1B3，1，1C0，1，2D1，0，1，2【分析】化简集合B，根据交集的定义写出AB【解
7、答】解：集合Ax|x2k1，kz为奇数集，Bx|x2x60x|2x3，则AB1，1故选：A【点评】本题考查了集合的化简与运算问题，是基础题2（5分）一路口的红绿灯，红灯的时间为30秒，黄灯的时间为5秒，绿灯的时间为40秒当你到达此路口时，看见的不是绿灯的概率为（）ABCD【分析】用几何概型的概率公式计算即可【解答】解：由题意知红灯的时间为30秒，黄灯的时间为5秒，绿灯的时间为40秒；到达此路口时看见的不是绿灯的概率为P1故选：C【点评】本题考查了几何概型的概率计算问题，是基础题3（5分）已知命题p：x1，x2R，（f（x1）f（x2）（x1x2）0，则p是（）Ax1，x2R，（f（x1）f（x
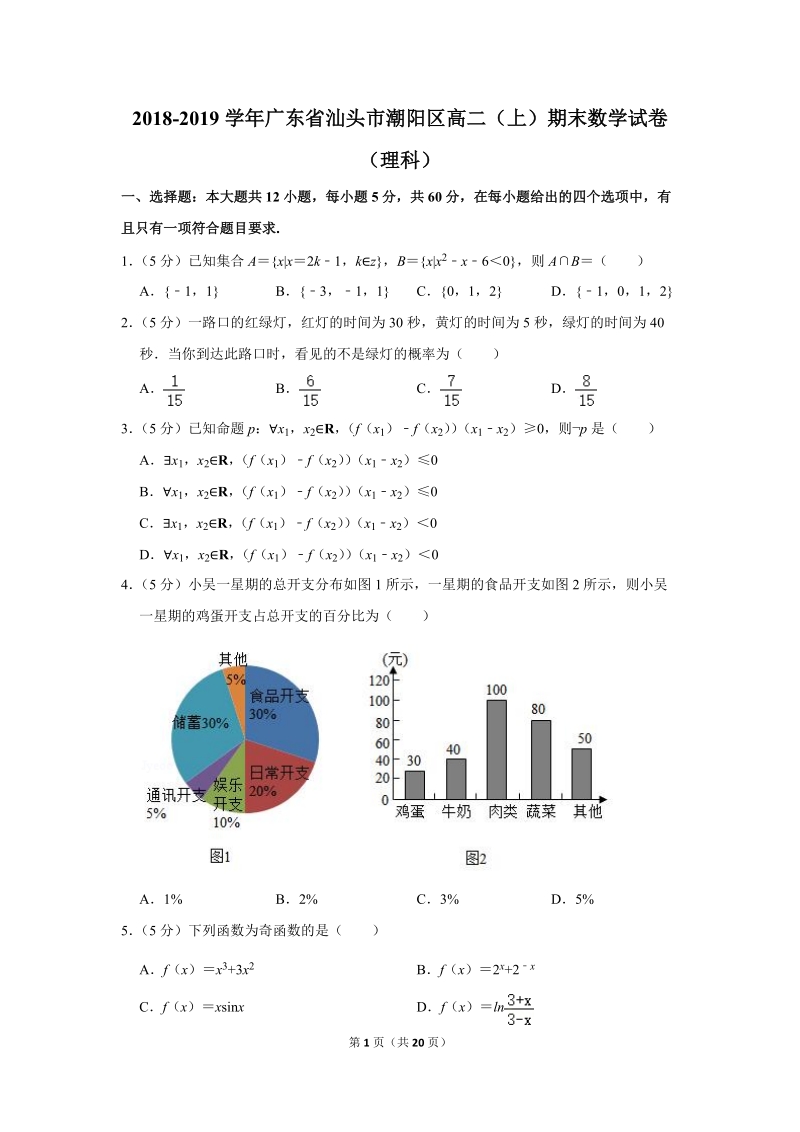
8、2）（x1x2）0Bx1，x2R，（f（x1）f（x2）（x1x2）0Cx1，x2R，（f（x1）f（x2）（x1x2）0Dx1，x2R，（f（x1）f（x2）（x1x2）0【分析】由全称命题的否定是特称命题，写出命题p的否定p来【解答】解：根据全称命题的否定是特称命题，得；命题p的否定是p：x1，x2R，（f（x1）f（x2）（x1x2）0故选：C【点评】本题考查了全称命题的否定命题是什么，解题时直接写出它的否定命题即可，是容易题4（5分）小吴一星期的总开支分布如图1所示，一星期的食品开支如图2所示，则小吴一星期的鸡蛋开支占总开支的百分比为（）A1%B2%C3%D5%【分析】由图1知食品开支
9、占总开支的30%，由图2知鸡蛋开支占食品开支的，由此求得鸡蛋开支占总开支的百分比【解答】解：由图1所示，食品开支占总开支的30%，由图2所示，鸡蛋开支占食品开支的，鸡蛋开支占总开支的百分比为30%3%故选：C【点评】本题考查了频率分布应用问题，是基础题5（5分）下列函数为奇函数的是（）Af（x）x3+3x2Bf（x）2x+2xCf（x）xsinxDf（x）ln【分析】举例说明A不是奇函数，利用定义证明B，C为偶函数，D为奇函数【解答】解：对于A，f（1）2，f（1）4，f（1）f（1），函数不是奇函数；对于B，函数定义域为R，f（x）2x+2（x）2x+2xf（x），函数为偶函数；对于C，函数
10、定义域为R，f（x）xsin（x）xsinxf（x），函数为偶函数；对于D，由0，得3x3，函数定义域为（3，3），而f（x），函数为奇函数故选：D【点评】本题考查函数奇偶性的性质与判断，训练了利用定义法判断函数的奇偶性，是基础题6（5分）函数f（x）sinxcosx在下列哪个区间上是单调递减的（）A，0B0，CD【分析】化函数f（x）为正弦型函数，再根据正弦函数的性质求f（x）的单调减区间【解答】解：函数f（x）sinxcosxsin（x），令+2kx+2k，kZ；解得+2kx+2k，kZ；令k0，得x，f（x）在区间，上是单调减函数故选：D【点评】本题考查了正弦函数的图象与性质的应用问题，
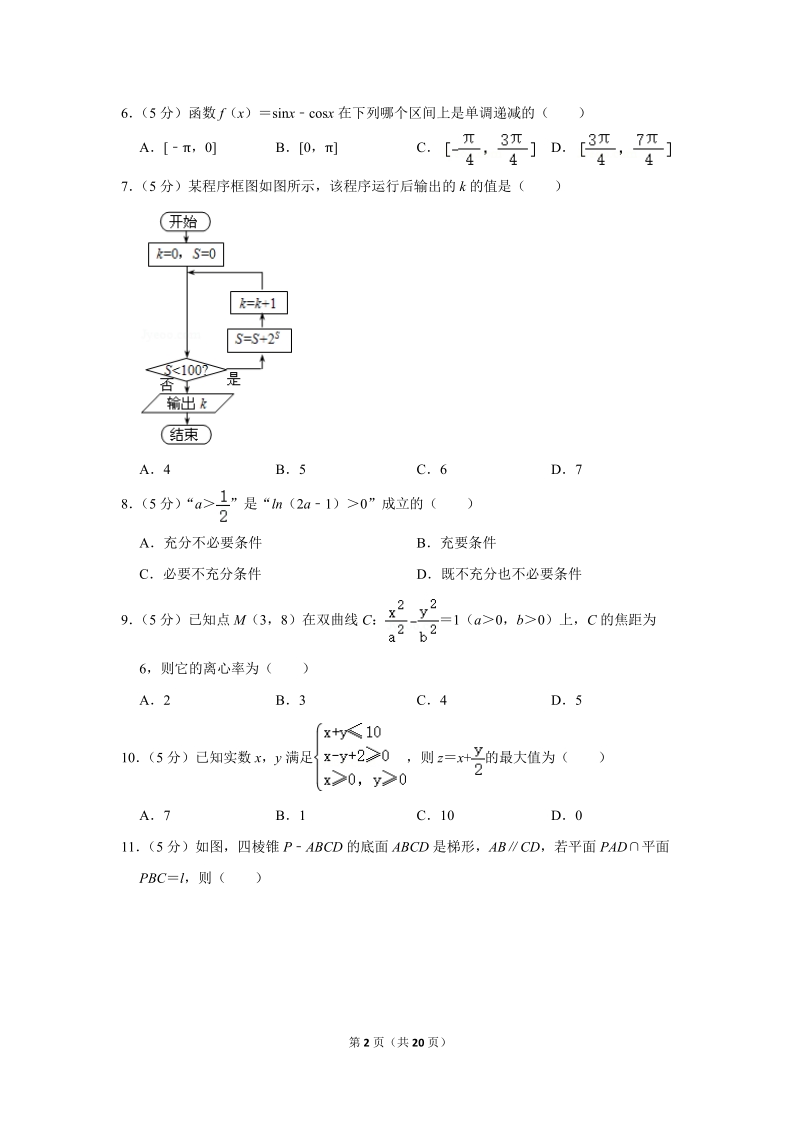
11、是基础题7（5分）某程序框图如图所示，该程序运行后输出的k的值是（）A4B5C6D7【分析】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量k的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案【解答】解：当S0时，满足继续循环的条件，故S1，k1；当S1时，满足继续循环的条件，故S3，k2；当S3时，满足继续循环的条件，故S11，k3；当S11时，满足继续循环的条件，故S2059，k4；当S2049时，不满足继续循环的条件，故输出的k值为4，故选：A【点评】本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答8（5分）“a”是“ln（
12、2a1）0”成立的（）A充分不必要条件B充要条件C必要不充分条件D既不充分也不必要条件【分析】由ln（2a1）0得a1，再根据小范围推出大范围得结果【解答】解：ln（2a1）0，2a11，a1，a推不出a1，a1a，“a”是“ln（2a1）0”的必要不充分条件故选：C【点评】本题考查了充分条件和必要条件的判断，考查了推理能力与计算能力，属于基础题9（5分）已知点M（3，8）在双曲线C：1（a0，b0）上，C的焦距为6，则它的离心率为（）A2B3C4D5【分析】由M在双曲线上，代入双曲线方程，又c3，即a2+b29，解方程可得a，由离心率公式可得所求值【解答】解：点M（3，8）在双曲线C：1（a
13、0，b0）上，可得1，C的焦距为6，即2c6，可得c3，即a2+b29由解得a1，b2，则e3，故选：B【点评】本题考查双曲线的方程和性质，考查离心率的求法，注意运用方程思想，考查运算能力，属于基础题10（5分）已知实数x，y满足，则zx+的最大值为（）A7B1C10D0【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案【解答】解：由约束条件作出可行域如图，A（10，0），化目标函数zx+为y2x+2z，由图可知，当直线y2x+2z过点A时，直线在y轴上的截距最大，z有最大值为10故选：C【点评】本题考查简单的线性规划
14、，考查了数形结合的解题思想方法，是中档题11（5分）如图，四棱锥PABCD的底面ABCD是梯形，ABCD，若平面PAD平面PBCl，则（）AlCDBlBCCl与直线AB相交Dl与直线DA相交【分析】可得AD与CB必相交于点M，则P是面平面PAD和平面PBC的公共点，又平面PAD平面PBCl【解答】解：四棱锥PABCD的底面ABCD是梯形，ABCDAD与CB必相交于点M，则P是面平面PAD和平面PBC的公共点，又平面PAD平面PBClPll与直线DA相交故选：D【点评】本题考查了空间几何体中的直线与平面的位置关系，属于中档题12（5分）若曲线与直线ykx1有两个不同的交点，则实数k的取值范围是（
15、）ABCD【分析】作出两个函数的图象，利用数形结合即可得到结论【解答】解：作出曲线 y的图象如图：直线ykx1过定点（0，1），当k0时，两个函数只有一个交点，不满足条件，当k0时，两个函数有2个交点，满足条件，当k0时，直线ykx1与y在x1相切时，两个函数只有一个交点，此时kx1，即kx2（1+k）x+30，判别式（1+k）212k0，解得k210k+10，k52或k5+2（舍去）综上满足条件的k的取值范围是（，0）（0，52），故选：D【点评】本题主要考查函数与方程的应用，利用数形结合以及分段函数的性质是解决本题的关键二、填空题：本大题共4小题，每小题5分，共20分13（5分）已知地球表
16、面及约是火星表面积的4倍，则地球体积是火星体积的8倍【分析】先利用已知条件得出地球半径与火星半径的倍数关系，再利用球体体积公式得出地球体积与火星体积的倍数关系【解答】解：设地球的半径为R，火星的半径为r，由已知条件得4R244r2，所以，R2r，所以，地球的体积为，因此，地球体积是火星体积的8倍，故答案为：8倍【点评】本题考查球体的表面积与体积，确定地球与火星半径之间的倍数关系，是解本题的关键，属于基础题14（5分）已知向量，间的夹角为，若（2，3），|，则【分析】可求出，并且，向量，间的夹角为，这样进行数量积的计算即可求出【解答】解：，且，间的夹角为；故答案为：【点评】考查根据向量坐标求向量
17、长度的方法，以及向量数量积的计算公式15（5分）九章算术中，将底面是直角三角形的直三棱柱称之为“堑堵”已知某“堑堵“的三视图如图所示，俯视图中间的实线平分矩形的面积，则该“堑堵”的表面积为6+4【分析】首先把几何体的三视图转换为几何体，进一步利用几何体的表面积公式求出结果【解答】解：根据几何体的三视图，如图所示：转换为几何体为：底面为腰长为的等腰直角三角形，高为2的三棱柱故：+6+4故答案为：6+4【点评】本题考查的知识要点：三视图和几何体的转换，几何体的体积和表面积公式的应用，主要考查学生的运算能力和转化能力，属于基础题型16（5分）已知抛物线y24x的焦点为F，点A（5，3），M为抛物线上
18、一点且M不在直线AF上，则MAF周长的最小值为11【分析】当MAx轴时，|MF|+|MA|取得最小值，从而得出三角形周长的最小值【解答】解：F（1，0），|AF|5，过M向抛物线的准线x1作垂线，垂足为B，则|MF|MB|，当A，B，M三点共线时，|MA|+|MB|取得最小值5+16，即|MF|+|MA|的最小值为6，MAF周长的最小值为为11故答案为：11【点评】本题考查了抛物线的定义与性质，属于中档题三、解答题：本大题共70分，解答应写出文字说明、证明过程或演算步骤17（10分）已知在ABC中，角A，B，C所对的边分别为且a，b，c，且（1）求角A的大小；（2）若a6，sinB2sinC，
19、求ABC的面积【分析】（1）直接利用三角函数关系式和正弦定理的应用求出结果（2）利用余弦定理和三角形的面积公式求出结果【解答】解：（1）在ABC中，角A，B，C所对的边分别为且a，b，c，且则：，整理得：，则：tanA，由于：0A，解得：A（2）a6，sinB2sinC，所以：b2c，所以：a2b2+c22bccosA，整理得：364c2+c22c2，解得：c所以b则：【点评】本题考查的知识要点：三角函数关系式的恒等变换，正弦定理和余弦定理及三角形面积公式的应用18（12分）已知圆的方程为：（x1）2+y21求：（1）斜率为3且与圆相切直线的方程；（2）过定点（2，3）且圆相切的直线的方程【分
20、析】（1）设斜率为3且与圆相切的直线方程，利用圆心到直线的距离dr求得切线方程；（2）设过定点且与圆相切的直线方程，利用圆心到直线的距离dr求得切线方程，注意斜率不存在时的情况【解答】解：（1）圆的方程为：（x1）2+y21，设斜率为3且与圆相切的直线方程为y3x+b，则圆心C（1，0）到该直线的距离为d1，解得b3，y3x3+或y3x3；（2）设过定点（2，3）且与圆相切的直线方程为y+3k（x2），即kxy2k30，则圆心C到该直线的距离为d1，解得k，切线方程为y+3（x2），即4x+3y+10；又当斜率k不存在时，直线x2也是圆的切线；综上，所求圆的切线为x2或4x+3y+10【点评】
21、本题考查了直线与圆相切的情况与应用问题，是基础题19（12分）已知正项的等比数列an的前n项和为Sn，且（1）求数列an的通项公式；（2）若bnlog2an+3，数列的前n项和为Tn，求满足的正整数n的最小值【分析】（1）正项的等比数列an的公比为q（q0），由等比数列的通项公式，解方程可得首项和公比，即可得到所求通项公式；（2）求得bnlog2an+3log22n2+3n2+3n+1，运用裂项相消求和可得Tn，解不等式即可得到所求最小值【解答】解：（1）正项的等比数列an的公比为q（q0），可得2a1qa1+a1q+，a1q22，解得a1，q2，则ana1qn12n2；（2）bnlog2an
22、+3log22n2+3n2+3n+1，前n项和为Tn+，满足，可得，解得n4，满足的正整数n的最小值为5【点评】本题考查等比数列的通项公式的运用，考查数列的求和方法：裂项相消求和，不等式的解法，考查运算能力属于中档题20（12分）如图，四边形PDCE为矩形，四边形ABCD为梯形，平面PDCE平面ABCD，BADADC90，ABADCDa，PDa，M为PA中点（1）求证：AC平面MDE；（2）求直线ME与平面PBC所成角的正弦值【分析】（1）连结PC，交DE于N，连结MN，推导出MNAC，由此能证明AC平面MDE（2）以D为原点，DA，DB，DP所在直线为x，y，z轴，建立空间直角坐标系，利用向
23、量法能求出直线ME与平面PBC所成角的正弦值【解答】证明：（1）连结PC，交DE于N，连结MN，在PAC中，M，N分别为PA，PC的中点，MNAC，AC平面MDE，MN平面MDE，AC平面MDE解：（2）以D为原点，DA，DB，DP所在直线为x，y，z轴，建立空间直角坐标系，则P（0，0，），B（a，a，0），C（0，2a，0），A（a，0，0），M（），E（0，2a，），（a，a，），（a，a，0），设平面PBC的法向量（x，y，z），则，取z1，得（，1），（，2a，a），设直线ME与平面PBC所成角为，则sin|cos|，直线ME与平面PBC所成角的正弦值为【点评】本题考查线面平行的证明
24、，考查线面角的正弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题21（12分）设函数f（x）（1）当a2时，求f（x）的单调区间；（2）当a0时，求不等式f（x）0的解集【分析】（1）a2时，根据一次函数和二次函数的单调性即可找出f（x）的单调区间；（2）a0时，可将原不等式转化为，或，然后可将a分成0a1和a1两种情况，分别解出不等式组，的解，再求并集即可【解答】解：（1）a2时，；根据一次函数和二次函数的单调性得，f（x）在（，1，（1，+）上单调递减；f（x）的单调递减区间为（，1，（1，+）；（2）a0时，不等式转化为，或；若0
25、a1时，解得，xa；解得，x1，不等式的解集为（，a）（1，+）；若a1时，解得，x1；解得，xa，不等式的解集为（，1（a，+）【点评】考查分段函数的单调性的判断，一次函数和二次函数的单调性，以及一元二次不等式的解法22（12分）已知椭圆+1（ab0）的左、右焦点分别为F1，F2，离心率e，点P是椭圆上的一个动点，PF1F2面积的最大值是4（1）求椭圆的方程；（2）若A，B，C，D是椭圆上不重合的四点，AC与BD相交于点F1，且AC与BD垂直，又|AC|+|BD|，求此时直线AC的方程【分析】（1）由椭圆的离心率公式和当P位于椭圆的短轴的端点时，PF1F2面积取得最大值，由三角形的面积公式和
26、基本量的关系，解方程可得a，b，进而得到所求椭圆方程；（2）讨论直线AC，BD的斜率是否存在，设出直线方程，联立椭圆方程，运用弦长公式，解方程即可得到所求方程【解答】解：（1）由题意可得e，当P位于椭圆的短轴的端点时，PF1F2面积的最大值是4，即有b2c4，又a2b2c2，解得a4，b2，则椭圆方程为+1；（2）由（1）知F1（2，0），ACBD，当直线AC，BD中一条直线斜率不存在时，|AC|+|BD|14，不合题意；当直线AC斜率为k，k0时，其方程为yk（x+2），将该方程带入椭圆方程并整理得（3+4k2）x2+16k2x+16k2480，若设A（x1，y1），B（x2，y2），则x1+x2，x1x2，|AC|x1x2|；直线BD的方程为y（x+2），同理可得|BD|；|AC|+|BD|，解得k21，即直线AC的方程为y（x+2）【点评】本题考查三角形的面积公式，椭圆离心率的概念，椭圆的标准方程，a，b，c三个系数的几何意义，直线的点斜式方程，以及弦长公式，属于中档题
