1、2020中考备考训练圆一选择题（共13小题）1如图，以点P为圆心作圆，所得的圆与直线l相切的是（）A以PA为半径的圆B以PB为半径的圆C以PC为半径的圆D以PD为半径的圆2已知圆锥的底面半径为2cm，母线长为3cm，则它的侧面展开图的面积为（）A18cm2B12cm2C6cm2D3cm23如图，O是ABC的外接圆，AD是O的直径，若O的半径为5，AC8则cosB的值是（）ABCD4九章算术是我国古代内容极为丰富的数学名著，书中有这样一个问题：“今有勾八步，股十五步，问勾中容圆，径几何？”其意思是：“如图，今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆
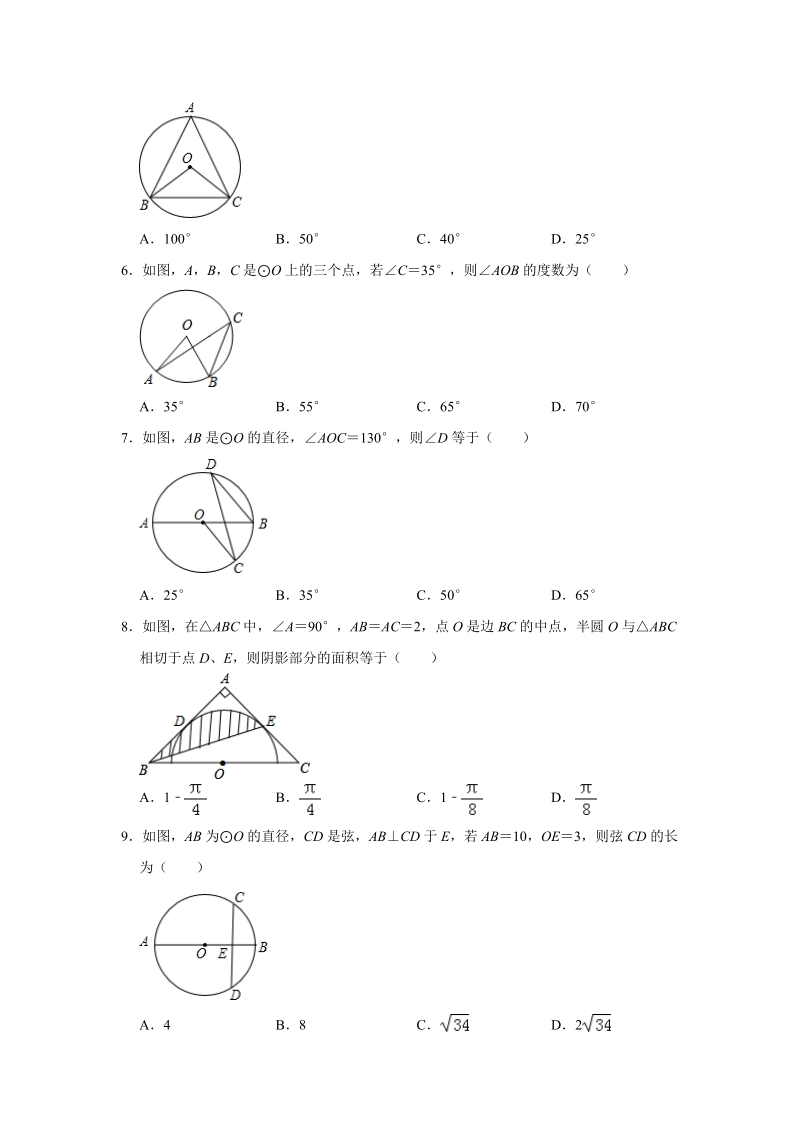
2、形（内切圆）直径是多少？”此问题中，该内切圆的直径是（）A5步B6步C8步D10步5如图，在O中，BOC100，则A等于（）A100B50C40D256如图，A，B，C是O上的三个点，若C35，则AOB的度数为（）A35B55C65D707如图，AB是O的直径，AOC130，则D等于（）A25B35C50D658如图，在ABC中，A90，ABAC2，点O是边BC的中点，半圆O与ABC相切于点D、E，则阴影部分的面积等于（）A1BC1D9如图，AB为O的直径，CD是弦，ABCD于E，若AB10，OE3，则弦CD的长为（）A4B8CD210如图，若AB是O的直径，CD是O的弦，ABD58，则C的度
3、数为（）A116B58C42D3211如图，O的半径OC垂直于弦AB，D是优弧AB上的一点（不与点A、B重合），若AOC50，则CDB等于（）A25B30C40D5012如图，等边三角形ABC内接于O，连接OB，OC，那么BOC的度数是（）A150B120C90D6013如图，AB为O直径，CD为O的弦，ACD28，则BAD的度数为（）A28B56C62D72二填空题（共15小题）14若圆锥的底面半径是10，侧面展开图是一个半圆，则该圆锥的母线长为 15如图，PA，PB是O的切线，A，B为切点，AC是O的直径，BAC15，则P的度数为 16如图所示的网格是正方形网格，线段AB绕点A顺时针旋转（
4、0180）后与O相切，则的值为 17阅读下面材料：在数学课上，老师提出利用尺规作图完成下面问题：已知：ACB是ABC的一个内角求作：APBACB小明的做法如下：如图作线段AB的垂直平分线m；作线段BC的垂直平分线n，与直线m交于点O；以点O为圆心，OA为半径作ABC的外接圆；在弧ACB上取一点P，连结AP，BP所以APBACB老师说：“小明的作法正确”请回答：（1）点O为ABC外接圆圆心（即OAOBOC）的依据是 ；（2）APBACB的依据是 18如图，正六边形ABCDEF内接于O，O的半径为1，则的长为 19如图，O的半径为6，OA与弦AB的夹角是30，则弦AB的长度是 20如图，在扇形OA
5、B中，AOB90，OA3，将扇形OAB绕点A逆时针旋转n（0n180）后得到扇形OAB，当点O在弧AB上时，n为 ，图中阴影部分的面积为 21两圆半径分别为3cm和7cm，当圆心距为9cm时，两圆的位置关系是 22若圆锥的底面周长为2cm，将其展开后所得扇形的半径为6cm，则圆锥的侧面积为 cm223如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型若该圆的半径为1，扇形的圆心角等于60，则这个扇形的半径R的值是 24如图，梯形ABCD中，ADBC，C90，ABAD4，BC6，以A为圆心在梯形内画出一个最大的扇形（图中阴影部分）的面积是 25李红同学为了在新年晚会上表演节目，
6、她利用半径为40cm的扇形纸片制作一个圆锥形纸帽（如图，接缝处不重叠），如果圆锥底面半径为10cm，那么这个圆锥的侧面积是 cm226如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，P为切点，如果AB8cm，小圆半径为3cm，那么大圆半径为 cm27如图，PA、PB切O于点A、B，点C是O上一点，且ACB65，则P 度28已知：如图，在22的网格中，每个小正方形的边长都是1，图中的阴影部分图案是由一个点为圆心，半径分别为1和2的圆弧围成，则阴影部分的面积为 三解答题（共22小题）29一些不便于直接测量的圆形孔道的直径可以用如下方法测量如图，把一个直径为10mm的小钢球紧贴在孔道边缘
7、，测得钢球顶端离孔道外端的距离为8mm，求这个孔道的直径AB30如图，在RtABE中，B90，以AB为直径的O交AE于点C，CE的垂直平分线FD交BE于点D，连接CD（1）判断CD与O的位置关系，并证明；（2）若ACAE12，求O的半径31数学课上学习了圆周角的概念和性质：“顶点在圆上，两边与圆相交”，“同弧所对的圆周角相等”，小明在课后继续对圆外角和圆内角进行了探究下面是他的探究过程，请补充完整：定义概念：顶点在圆外，两边与圆相交的角叫做圆外角，顶点在圆内，两边与圆相交的角叫做圆内角如图1，M为所对的一个圆外角（1）请在图2中画出所对的一个圆内角；提出猜想（2）通过多次画图、测量，获得了两个
8、猜想：一条弧所对的圆外角 这条弧所对的圆周角；一条弧所对的圆内角 这条弧所对的圆周角；（填“大于”、“等于”或“小于”）推理证明：（3）利用图1或图2，在以上两个猜想中任选一个进行证明；问题解决经过证明后，上述两个猜想都是正确的，继续探究发现，还可以解决下面的问题（4）如图3，F，H是CDE的边DC上两点，在边DE上找一点P使得FPH最大请简述如何确定点P的位置（写出思路即可，不要求写出作法和画图）32如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分如果M是O中弦CD的中点，EM经过圆心O交O于点E，CD10，EM25求O的半径33如图，AB是O的直径，C，D是O上两点，且，过点C的
9、直线CFAD于点F，交AB的延长线于点E，连接AC（1）求证：EF是O的切线；（2）连接FO，若sinE，O的半径为r，请写出求线段FO长的思路34九章算术是中国传统数学重要的著作，奠定了中国传统数学的基本框架九章算术中记载：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，间径几何？”（如图）阅读完这段文字后，小智画出了一个圆柱截面示意图（如图），其中BOCD于点A，求间径就是要求O的直径再次阅读后，发现AB 寸，CD 寸（一尺等于十寸），通过运用有关知识即可解决这个问题请你补全题目条件，并帮助小智求出O的直径35如图，已知ABC是等边三角形，以AB为直径作O，交BC边于点D，交
10、AC边于点F，作DEAC于点E（1）求证：DE是O的切线；（2）若ABC的边长为4，求EF的长度36如图，在平面直角坐标系中，直径为2的A经过坐标系原点O（0，0），与x轴交于点B，与y轴交于点C（0，）（1）求点B的坐标；（2）如图，过点B作A的切线交直线OA于点P，求点P的坐标；（3）过点P作A的另一条切线PE，请直接写出切点E的坐标37如图，在平面直角坐标系xOy中，以点A（2，3）为圆心的A交x轴于点B，C，BC8，求A的半径38如图，在ABC中，BABC，以AB为直径的O分别交AC，BC于点D，E，BC的延长线与O的切线AF交于点F（1）求证：ABC2CAF；（2）若AC2，CE：E
11、B1：4，求CE，AF的长39如图，方格纸中每个小正方形的边长均为1，ABC的顶点均在小正方形的顶点处（1）以点A为旋转中心，把ABC顺时针旋转90，画出旋转后的ABC；（2）在（1）的条件下，求点C运动到点C所经过的路径长40如图，O的半径为3，点P是弦AB延长线上的一点，连接OP，若OP4，P30，求弦AB的长41如图，AB是O的直径，弦CDAB于点H，点G在弧BD上，连接AG，交CD于点K，过点G的直线交CD延长线于点E，交AB延长线于点F，且EGEK（1）求证：EF是O的切线；（2）若O的半径为13，CH12，ACEF，求OH和FG的长42在平面直角坐标系中，等腰RtOAB斜边OB在y
12、轴上，且OB4（1）画出OAB绕原点O顺时针旋转90后得到的三角形OAB；（2）求点A在旋转过程中经过的路径长43如图，DE是O的直径，CE与O相切，E为切点连接CD交O于点B，在EC上取一个点F，使EFBF（1）求证：BF是O的切线；（2）若SAMCSAMO+SOMCSAOC，DE9，求BF的长44已知：O是ABC的外接圆，ABAC，点M为O上一点，且在弦BC下方（1）如图，若ABC60，BM1，CM3，则AM的长为 ；（2）如图，若ABC45，BM1，CM3，则AM的长为 ；（3）如图，若ABC30，BM1，CM3，则AM的长为 ；（4）如图，若ABCn，BMa，CMb，（其中ab），求出
13、AM的长（答案用含有a，b及n的三角函数的代数式表示）45如图，CD与AB是O内两条相交的弦，且AB为O的直径，CEAB于点E，CE5，连接AC、BD（1）若，则cosA ；（2）在（1）的条件下，求BE的长46如图，在ABC中，ACB90，O为BC边上一点，以O为圆心，OB为半径作半圆与AB边和BC边分别交于点D、点E，连接CD，且CDCA，BD，tanADC2（1）求证：CD是半圆O的切线；（2）求半圆O的直径；（3）求AD的长47如图所示的直面直角坐标系中，OAB的三个顶点坐标分别为O（0，0），A（1，3）B（3，2）（1）将OAB绕原点O逆时针旋转90画出旋转后的OAB；（2）求出点
14、B到点B所走过的路径的长48如图，在矩形ABCD中，点O在对角AC上，以OA长为半径的O与AD、AC分别交于点E、F，且ACBDCE（1）求证：CE是O的切线；（2）若，AE7，求O的直径49在ABC中，A90，AB4，AC3，M是AB上的动点（不与A，B重合），过M点作MNBC交AC于点N以MN为直径作O，并在O内作内接矩形AMPN令AMx（1）用含x的代数式表示MNP的面积S；（2）当x为何值时，O与直线BC相切；（3）在动点M的运动过程中，记MNP与梯形BCNM重合的面积为y，试求y关于x的函数表达式，并求x为何值时，y的值最大，最大值是多少？50已知：如图，ABC内接于O，连接AO并延
15、长交BC于点D，若AO5，BC8，ADB90，求ABC的面积2020中考备考训练圆参考答案与试题解析一选择题（共13小题）1如图，以点P为圆心作圆，所得的圆与直线l相切的是（）A以PA为半径的圆B以PB为半径的圆C以PC为半径的圆D以PD为半径的圆【分析】根据直线与圆的位置关系的判定方法进行判断【解答】解：PBl于B，以点P为圆心，PB为半径的圆与直线l相切故选：B【点评】本题考查了直线与圆的位置关系：判断直线和圆的位置关系：设O的半径为r，圆心O到直线l的距离为d若直线l和O相交dr；直线l和O相切dr；直线l和O相离dr2已知圆锥的底面半径为2cm，母线长为3cm，则它的侧面展开图的面积为
16、（）A18cm2B12cm2C6cm2D3cm2【分析】利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算【解答】解：它的侧面展开图的面积2236（cm2）故选：C【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长3如图，O是ABC的外接圆，AD是O的直径，若O的半径为5，AC8则cosB的值是（）ABCD【分析】连接CD，则可得ACD90，且BD，在RtADC中可求得CD，则可求得cosD，即可求得答案【解答】解：如图，连接CD，ADO的直径，ACD90，且BD，在R
17、tACD中，AD5210，AC8，CD6，cosD，cosBcosD，故选：B【点评】本题主要考查圆周角定理及三角函数的定义，构造直角三角形是解题的关键4九章算术是我国古代内容极为丰富的数学名著，书中有这样一个问题：“今有勾八步，股十五步，问勾中容圆，径几何？”其意思是：“如图，今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆形（内切圆）直径是多少？”此问题中，该内切圆的直径是（）A5步B6步C8步D10步【分析】由勾股定理可求得斜边长，分别连接圆心和三个切点，设内切圆的半径为r，利用面积相等可得到关于r的方程，可求得内切圆的半径，则可求得内切圆的直径
18、【解答】解：如图，在RtABC中，AC8，BC15，C90，AB17，SABCACBC81560，设内切圆的圆心为O，分别连接圆心和三个切点，及OA、OB、OC，设内切圆的半径为r，SABCSAOB+SBOC+SAOCr（AB+BC+AC）20r，20r60，解得r3，内切圆的直径为6步，故选：B【点评】本题主要考查三角形的内切圆，连接圆心和切点，把三角形的面积分成三个三个角形的面积得到关于r的方程是解题的关键5如图，在O中，BOC100，则A等于（）A100B50C40D25【分析】根据圆周角定理可求得A50【解答】解：BOC100，ABOC50故选：B【点评】本题利用了圆周角定理：在同圆或
19、等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半6如图，A，B，C是O上的三个点，若C35，则AOB的度数为（）A35B55C65D70【分析】由A，B，C是O上的三个点，若C35，直接利用圆周角定理求解即可求得答案【解答】解：A，B，C是O上的三个点，C35，AOB2C70故选：D【点评】此题考查了圆周角定理此题比较简单，注意掌握数形结合思想的应用7如图，AB是O的直径，AOC130，则D等于（）A25B35C50D65【分析】由AB是O的直径，AOC130，可得BOC180AOC50，然后由圆周角定理即可求得答案【解答】解：AB是O的直径，AOC130，BOC180AOC
20、50，DBOC25故选：A【点评】此题考查了圆周角定理此题难度不大，注意掌握数形结合思想的应用8如图，在ABC中，A90，ABAC2，点O是边BC的中点，半圆O与ABC相切于点D、E，则阴影部分的面积等于（）A1BC1D【分析】首先连接OD，OE，易得BDFEOF，继而可得S阴影S扇形DOE，即可求得答案【解答】解：连接OD，OE，半圆O与ABC相切于点D、E，ODAB，OEAC，在ABC中，A90，ABAC2，四边形ADOE是正方形，OBD和OCE是等腰直角三角形，ODOEADBDAEEC1，ABCEOC45，ABOE，DBFOEF，在BDF和EOF中，BDFEOF（AAS），S阴影S扇形D
21、OE12故选：B【点评】此题考查了扇形的面积，切线的性质、全等三角形的判定与性质以及正方形的性质此题难度适中，注意掌握数形结合思想的应用9如图，AB为O的直径，CD是弦，ABCD于E，若AB10，OE3，则弦CD的长为（）A4B8CD2【分析】连接OC，由AB的长求出半径OC的长，根据AB与CD垂直，利用垂径定理得到E为CD的中点，在直角三角形COE中，由OC与OE的长，利用勾股定理求出CE的长，即可确定出CD的长【解答】解：连接OC，直径AB10，OC5，ABCD，E为CD的中点，即CEDECD，在RtOCE中，OC5，OE3，根据勾股定理得：CE4，则CD2CE8故选：B【点评】此题考查了
22、垂径定理，以及勾股定理，熟练掌握定理是解本题的关键10如图，若AB是O的直径，CD是O的弦，ABD58，则C的度数为（）A116B58C42D32【分析】由AB是O的直径，推出ADB90，再由ABD58，求出A32，根据圆周角定理推出C32【解答】解：AB是O的直径，ADB90，ABD58，A32，C32故选：D【点评】本题主要考查圆周角定理，余角的性质，关键在于推出A的度数，正确的运用圆周角定理11如图，O的半径OC垂直于弦AB，D是优弧AB上的一点（不与点A、B重合），若AOC50，则CDB等于（）A25B30C40D50【分析】连接OB，根据垂径定理即可推出BOCAOC50，然后根据圆周
23、角定理即可推出CDB的度数【解答】解：连接OB，O的半径OC垂直于弦AB，AOC50，BOCAOC50，CDBBOC25故选A【点评】本题主要考查垂径定理，圆周角定理，关键在于正确的做出辅助线，求出BOCAOC5012如图，等边三角形ABC内接于O，连接OB，OC，那么BOC的度数是（）A150B120C90D60【分析】根据圆周角的定理可知，圆周角等于圆心角的一半，即可得出BOC2BAC，又ABC为等边三角形，可得A60，故可得出BOC120，即答案选B【解答】解：已知ABC为等边三角形，故A60，又ABC内接于O，A为圆周角，BOC为圆心角，故BOC2A120故选：B【点评】本题主要考查了
24、在圆内接三角形中圆周角定理，要求熟练掌握等边三角形的性质13如图，AB为O直径，CD为O的弦，ACD28，则BAD的度数为（）A28B56C62D72【分析】连接BD，根据直径所对的圆周角是直角，构造直角三角形ABD，再根据同弧所对的圆周角相等，求得B的度数，即可求得BAD的度数【解答】解：连接BDAB为O直径ADB90BACD28BAD90B62故选：C【点评】考查了圆周角定理的推论构造直径所对的圆周角是圆中常见的辅助线之一二填空题（共15小题）14若圆锥的底面半径是10，侧面展开图是一个半圆，则该圆锥的母线长为20【分析】侧面展开后得到一个半圆，半圆的弧长就是底面圆的周长依此列出方程即可【
25、解答】解：设母线长为x，根据题意得2x225，解得x10故答案为20【点评】本题考查了圆锥的计算，解题的关键是明白侧面展开后得到一个半圆就是底面圆的周长，难度不大15如图，PA，PB是O的切线，A，B为切点，AC是O的直径，BAC15，则P的度数为30【分析】先利用切线的性质得到CAP90，则利用互余计算出PAB75，再根据切线长定理得到PAPB，然后根据等腰三角形的性质和三角形内角和计算P的度数【解答】解：PA为切线，OAPA，CAP90，PAB90BAC901575，PA，PB是O的切线，PAPB，PBAPAB75，P180757530故答案为30【点评】本题考查了切线的性质：圆的切线垂直
26、于经过切点的半径16如图所示的网格是正方形网格，线段AB绕点A顺时针旋转（0180）后与O相切，则的值为60或120【分析】线段AB绕点A顺时针旋转（0180）后与O相切，切点为C和C，连接OC、OC，根据切线的性质得OCAB，OCAB，利用直角三角形30度的判定或三角函数求出OAC30，从而得到BAB60，同理可得OAC30，则BAB120【解答】解：线段AB绕点A顺时针旋转（0180）后与O相切，切点为C和C，连接OC、OC，则OCAB，OCAB，在RtOAC中，OC1，OA2，OAC30，BAB60，同理可得OAC30，BAB120，综上所述，的值为60或120故答案为60或120【点评
27、】本题考查了切线的性质：圆的切线垂直于经过切点的半径也考查了旋转的性质和直角三角形的性质17阅读下面材料：在数学课上，老师提出利用尺规作图完成下面问题：已知：ACB是ABC的一个内角求作：APBACB小明的做法如下：如图作线段AB的垂直平分线m；作线段BC的垂直平分线n，与直线m交于点O；以点O为圆心，OA为半径作ABC的外接圆；在弧ACB上取一点P，连结AP，BP所以APBACB老师说：“小明的作法正确”请回答：（1）点O为ABC外接圆圆心（即OAOBOC）的依据是线段垂直平分线上的点与这条线段两个端点的距离相等；等量代换；（2）APBACB的依据是同弧所对的圆周角相等【分析】（1）根据线段
28、的垂直平分线的性质定理以及等量代换即可得出结论（2）根据同弧所对的圆周角相等即可得出结论【解答】解：（1）如图2中，MN垂直平分AB，EF垂直平分BC，OAOB，OBOC（线段垂直平分线上的点与这条线段两个端点的距离相等），OAOBOC（等量代换）故答案为线段垂直平分线上的点与这条线段两个端点的距离相等；等量代换（2），APBACB（同弧所对的圆周角相等）故答案为同弧所对的圆周角相等【点评】本题考查作图复杂作图、线段的垂直平分线的性质、三角形的外心等知识，解题的关键是熟练掌握三角形外心的性质，属于中考常考题型18如图，正六边形ABCDEF内接于O，O的半径为1，则的长为【分析】求出圆心角AOB
29、的度数，再利用弧长公式解答即可【解答】解：ABCDEF为正六边形，AOB36060，的长为故答案为：【点评】此题将扇形的弧长公式与多边形的性质相结合，构思巧妙，利用了正六边形的性质19如图，O的半径为6，OA与弦AB的夹角是30，则弦AB的长度是6【分析】过O作OCAB于C，根据垂径定理求出AB2AC，根据含30角的直角三角形性质求出OC，根据勾股定理求出AC，即可得出答案【解答】解：过O作OCAB于C，OC过O，AB2AC，OA6，A30，OCOA3，由勾股定理得：AC3，AB2AC6故答案为：6【点评】本题考查了勾股定理，含30角的直角三角形性质，垂径定理的应用，能根据垂径定理得出AB2A
30、C是解此题的关键20如图，在扇形OAB中，AOB90，OA3，将扇形OAB绕点A逆时针旋转n（0n180）后得到扇形OAB，当点O在弧AB上时，n为60，图中阴影部分的面积为3【分析】连接OO，可知OOA为等边三角形，可求得n，连接AB、AB，可知弓形AB和弓形AB的面积相等，所以可知阴影部分的面积等于扇形BAB的面积，计算扇形BAB的面积可求得答案【解答】解：连接OO，由旋转的性质可知OAOA，又OOOA，OOA为等边三角形，n60，连接AB、AB，可知BAB60，S弓形AOBS弓形AOB，且AB3，S阴影S扇形BAB3故答案为：60；3【点评】本题主要考查旋转的性质及扇形的面积，由旋转得到
31、S弓形AOBS弓形AOB是解题的关键21两圆半径分别为3cm和7cm，当圆心距为9cm时，两圆的位置关系是相交【分析】由两圆半径分别为3cm和7cm，圆心距为9cm，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系【解答】解：两圆半径分别为3cm和7cm，两圆半径和为：3+710（cm），差为：734（cm），圆心距为9cm，两圆的位置关系是：相交故答案为：相交【点评】此题考查了圆与圆的位置关系注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系22若圆锥的底面周长为2cm，将其展开后所得扇形的半径为6cm，则圆锥的侧面积为6cm2【分析】侧面展开后
32、所得扇形的半径即为圆锥的母线长，那么圆锥的侧面积底面周长母线长，把相应数值代入即可求解【解答】解：圆锥的侧面积266cm2，故答案为：6【点评】本题考查了圆锥的计算，牢记圆锥的侧面积的计算方法是解题的关键23如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型若该圆的半径为1，扇形的圆心角等于60，则这个扇形的半径R的值是6【分析】圆的周长就是扇形的弧长，根据弧长的计算公式即可求得半径的长【解答】解：圆的周长212扇形的弧长为，2，解得：R6故答案为6【点评】本题主要考查三视图的知识和圆锥侧面面积的计算，正确理解圆的周长就是扇形的弧长是解题的关键24如图，梯形ABCD中，ADB
33、C，C90，ABAD4，BC6，以A为圆心在梯形内画出一个最大的扇形（图中阴影部分）的面积是4【分析】扇形面积公式：S，梯形的计算问题一般要转换成平行四边形和三角形的问题来解决【解答】解：过点A向BC作垂线，垂足为E，ADCE4，BC6，所以BE2，EAB30，DAB120，根据勾股定理可知AE216412，扇形面积为4【点评】主要考查了扇形的面积公式和梯形中的计算问题25李红同学为了在新年晚会上表演节目，她利用半径为40cm的扇形纸片制作一个圆锥形纸帽（如图，接缝处不重叠），如果圆锥底面半径为10cm，那么这个圆锥的侧面积是400cm2【分析】利用圆锥的侧面积公式可以直接求出面积【解答】解：
34、圆锥侧面积公式为：s侧面积rR1040400故填：400【点评】此题主要考查了圆锥的侧面积公式求法，注意公式的灵活应用26如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，P为切点，如果AB8cm，小圆半径为3cm，那么大圆半径为5cm【分析】连接OP，OA，根据切线的性质和垂径定理得到直角三角形OAP，在直角三角形中用勾股定理求出大圆的半径【解答】解：如图：连接OA，OP，AB是大O的切线，OPAB，且OP3，AP4，在RtOAP中，OA5大圆的半径是5cm故答案为：5【点评】本题考查的是切线的性质，利用切线的性质得到直角三角形，在直角三角形中用勾股定理计算求出大圆的半径27如图，
35、PA、PB切O于点A、B，点C是O上一点，且ACB65，则P50度【分析】连接OA，OB根据圆周角定理和四边形内角和定理求解【解答】解：连接OA，OBPA、PB切O于点A、B，则PAOPBO90，由圆周角定理知，AOB2C130，P+PAO+PBO+AOB360，P180AOB50【点评】本题利用了切线的概念，圆周角定理，四边形的内角和为360度求解28已知：如图，在22的网格中，每个小正方形的边长都是1，图中的阴影部分图案是由一个点为圆心，半径分别为1和2的圆弧围成，则阴影部分的面积为2【分析】若连接正方形的对角线，可发现阴影部分的面积是圆（以A为圆心、正方形边长为半径的圆）与正方形的面积差
36、，由此得解【解答】解：如图；S弓形OBS弓形OD，S阴影S扇形ABDSABD22222【点评】此题的计算过程并不复杂，关键是能够发现弓形OD和弓形OB的关系三解答题（共22小题）29一些不便于直接测量的圆形孔道的直径可以用如下方法测量如图，把一个直径为10mm的小钢球紧贴在孔道边缘，测得钢球顶端离孔道外端的距离为8mm，求这个孔道的直径AB【分析】先求出钢珠的半径及OD的长，连接OA，过点O作ODAB于点D，则AB2AD，在RtAOD中利用勾股定理即可求出AD的长，进而得出AB的长【解答】解：连接OA，过点O作ODAB于点D，则AB2AD，钢珠的直径是10mm，钢珠的半径是5mm，钢珠顶端离零
37、件表面的距离为8mm，OD3mm，在RtAOD中，AD4mm，AB2AD248mm【点评】本题考查的是垂径定理的应用及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键30如图，在RtABE中，B90，以AB为直径的O交AE于点C，CE的垂直平分线FD交BE于点D，连接CD（1）判断CD与O的位置关系，并证明；（2）若ACAE12，求O的半径【分析】（1）连接OC，由于FD是CE的垂直平分线，所以EDCE，又因为AOCA，A+E90，所以OCA+DCE90，所以CD与O相切（2）连接BC，易知ACB90，所以ACBABE，所以，由于ACAE12，所以OAAB，【解答】解：（1）连接
38、OC，如图1所示FD是CE的垂直平分线，DCDE，EDCE，OAOC，AOCA，RtABE中，B90，A+E90，OCA+DCE90，OCCD，CD与O相切（2）连接BC，如图2所示AB是O直径，ACB90，ACBABE，ACAE12，AB212，AB2，OA【点评】本题考查圆的综合问题，涉及垂直平分线的性质，圆周角定理，相似三角形的性质与判定等知识，需要学生灵活运用所学知识31数学课上学习了圆周角的概念和性质：“顶点在圆上，两边与圆相交”，“同弧所对的圆周角相等”，小明在课后继续对圆外角和圆内角进行了探究下面是他的探究过程，请补充完整：定义概念：顶点在圆外，两边与圆相交的角叫做圆外角，顶点在
39、圆内，两边与圆相交的角叫做圆内角如图1，M为所对的一个圆外角（1）请在图2中画出所对的一个圆内角；提出猜想（2）通过多次画图、测量，获得了两个猜想：一条弧所对的圆外角小于这条弧所对的圆周角；一条弧所对的圆内角大于这条弧所对的圆周角；（填“大于”、“等于”或“小于”）推理证明：（3）利用图1或图2，在以上两个猜想中任选一个进行证明；问题解决经过证明后，上述两个猜想都是正确的，继续探究发现，还可以解决下面的问题（4）如图3，F，H是CDE的边DC上两点，在边DE上找一点P使得FPH最大请简述如何确定点P的位置（写出思路即可，不要求写出作法和画图）【分析】（1）在O内任取一点M，连接AM，BM；（2）观察图形，可知：一条弧所对的圆外角小于这条弧所对的圆周角；一条弧所对的圆内角大于这条弧所对的圆周角，此问得解；（3）（i）BM与O相交于点C，连接AC，利用三角形外角的性质可得出ACBM+MAC，进而可证出ACBM；（ii）延长BM交O于点C，连接AC，利用三角形外角的性质可得出AMBACB+CAM，进而可证出AMBACB；（4）由（2）的结论，可知：当过点F，H的圆与DE相切时，切点即为所求的点P【解答】解：（1）如图2所示
