1、中考数学二轮复习重要考点精析方案设计题型一、中考专题诠释方案设计型问题，是指根据问题所提供的信息，运用学过的技能和方法，进行设计和操作，然后通过分析、计算、证明等，确定出最佳方案的一类数学问题。随着新课程改革的不断深入，一些新颖、灵活、密切联系实际的方案设计问题正越来越受到中考命题人员的喜爱，这些问题主要考查学生动手操作能力和创新能力，这也是新课程所要求的核心内容之一。二、解题策略和解法精讲方案设计型问题涉及生产生活的方方面面，如：测量、购物、生产配料、汽车调配、图形拼接等。所用到的数学知识有方程、不等式、函数、解直角三角形、概率和统计等知识。这类问题的应用性非常突出，题目一般较长，做题之前要
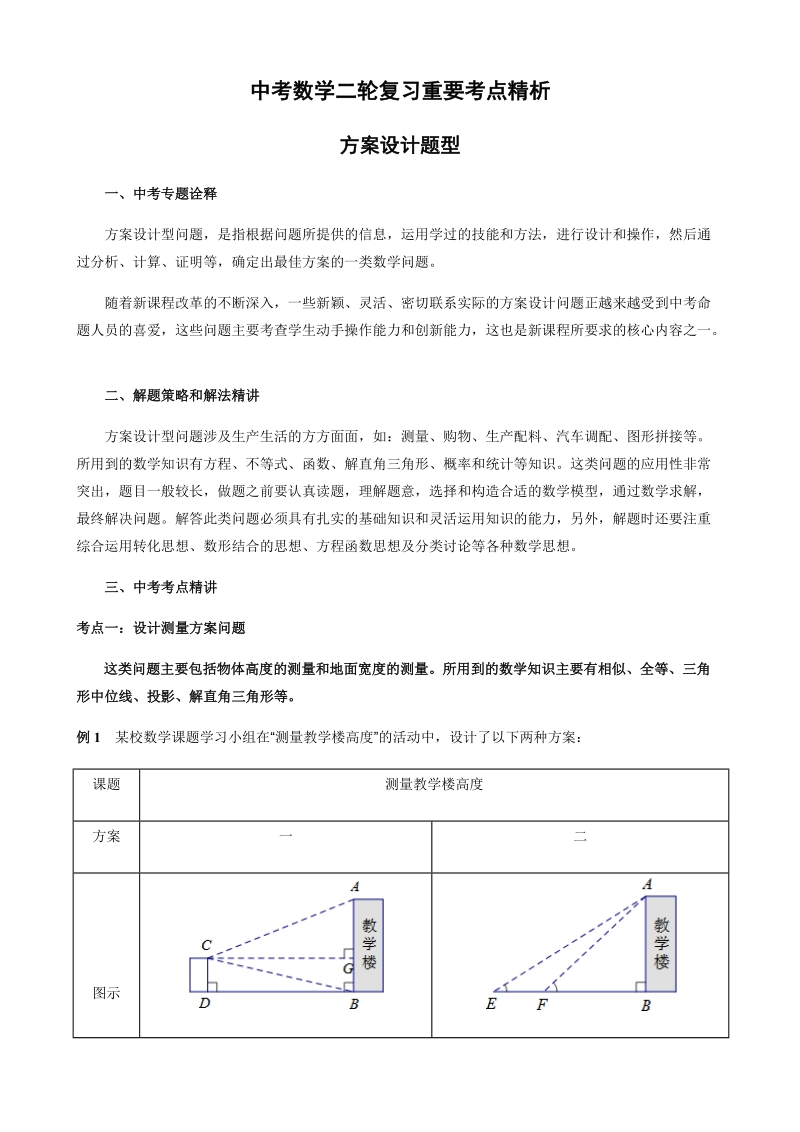
2、认真读题，理解题意，选择和构造合适的数学模型，通过数学求解，最终解决问题。解答此类问题必须具有扎实的基础知识和灵活运用知识的能力，另外，解题时还要注重综合运用转化思想、数形结合的思想、方程函数思想及分类讨论等各种数学思想。 三、中考考点精讲考点一：设计测量方案问题这类问题主要包括物体高度的测量和地面宽度的测量。所用到的数学知识主要有相似、全等、三角形中位线、投影、解直角三角形等。例1 某校数学课题学习小组在“测量教学楼高度”的活动中，设计了以下两种方案：课题测量教学楼高度方案一二图示测得数据CD=6.9m，ACG=22，BCG=13，EF=10m，AEB=32，AFB=43参考数据sin220
3、.37，cos220.93，tan220.40sin130.22，cos130.97tan130.23sin320.53，cos320.85，tan320.62sin430.68，cos430.73，tan430.93请你选择其中的一种方法，求教学楼的高度（结果保留整数）思路分析：若选择方法一，在RtBGC中，根据CG=即可得出CG的长，同理，在RtACG中，根据tanACG= 可得出AG的长，根据AB=AG+BG即可得出结论若选择方法二，在RtAFB中由tanAFB=可得出FB的长，同理，在RtABE中，由tanAEB=可求出EB的长，由EF=EB-FB且EF=10，可知 =10，故可得出A
4、B的长解：若选择方法一，解法如下：在RtBGC中，BGC=90，BCG=13，BG=CD=6.9，CG=30，在RtACG中，AGC=90，ACG=22，tanACG=，AG=30tan22300.40=12，AB=AG+BG=12+6.919（米）答：教学楼的高度约19米若选择方法二，解法如下：在RtAFB中，ABF=90，AFB=43，tanAFB=，FB=，在RtABE中，ABE=90，AEB=32，tanAEB=，EB=，EF=EB-FB且EF=10，-=10，解得AB=18.619（米）答：教学楼的高度约19米对应训练1如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他
5、们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60已知A点的高度AB为3米，台阶AC的坡度为1：（即AB：BC=1：），且B、C、E三点在同一条直线上请根据以上条件求出树DE的高度（侧倾器的高度忽略不计）解：如图，过点A作AFDE于F，则四边形ABEF为矩形，AF=BE，EF=AB=3，设DE=x，在RtCDE中，CE=x，在RtABC中，AB=3，BC=3，在RtAFD中，DF=DE-EF=x-3，AF=（x-3），AF=BE=BC+CE，（x-3）=3+x，解得x=9答：树高为9米考点二：设计搭配方案问题这类问题
6、不仅在中考中经常出现，大家在平时的练习中也会经常碰到。它一般给出两种元素，利用这两种元素搭配出不同的新事物，设计出方案，使获利最大或成本最低。解题时要根据题中蕴含的不等关系，列出不等式（组），通过不等式组的整数解来确定方案。例2 某校七年级准备购买一批笔记本奖励优秀学生，在购买时发现，每本笔记本可以打九折，用360元钱购买的笔记本，打折后购买的数量比打折前多10本（1）求打折前每本笔记本的售价是多少元？（2）由于考虑学生的需求不同，学校决定购买笔记本和笔袋共90件，笔袋每个原售价为6元，两种物品都打九折，若购买总金额不低于360元，且不超过365元，问有哪几种购买方案？思路分析：（1）设打折前
7、售价为x，则打折后售价为0.9x，表示出打折前购买的数量及打折后购买的数量，再由打折后购买的数量比打折前多10本，可得出方程，解出即可；（2）设购买笔记本y件，则购买笔袋（90-y）件，根据购买总金额不低于360元，且不超过365元，可得出不等式组，解出即可解：（1）设打折前售价为x，则打折后售价为0.9x，由题意得，解得：x=4，经检验得：x=4是原方程的根，答：打折前每本笔记本的售价为4元（2）设购买笔记本y件，则购买笔袋（90-y）件，由题意得，36040.9y+60.9（90-y）365，解得：67y70，x为正整数，x可取68，69，70，故有三种购买方案：方案一：购买笔记本68本，
8、购买笔袋22个；方案二：购买笔记本69本，购买笔袋21个；方案三：购买笔记本70本，购买笔袋20个；点评：本题考查了分式方程的应用、一元一次不等式组的应用，解答此类应用类题目，一定要先仔细审题，有时需要读上几遍，找到解题需要的等量关系或不等关系对应训练2 5月12日是母亲节，小明去花店买花送给母亲，挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花，已知康乃馨每支5元，兰花每支3元，小明只有30元，希望购买花的支数不少于7支，其中至少有一支是康乃馨（1）小明一共有多少种可能的购买方案？列出所有方案；（2）如果小明先购买一张2元的祝福卡，再从（1）中任选一种方案购花，求他能实现购买愿望的概
9、率解：（1）设购买康乃馨x支，购买兰花y支，由题意，得，x、y为正整数，当x=1时，y=6，7，8符合题意，当x=2时，y=5，6符合题意，当x=3时，y=4，5符合题意，当x=4时，y=3符合题意，当x=5时，y=1舍去，当x=6时，y=0舍去共有8种购买方案，方案1：购买康乃馨1支，购买兰花6支；方案2：购买康乃馨1支，购买兰花7支；方案3：购买康乃馨1支，购买兰花8支；方案4：购买康乃馨2支，购买兰花5支；方案5：购买康乃馨2支，购买兰花6支；方案6：购买康乃馨3支，购买兰花4支；方案7：购买康乃馨3支，购买兰花5支；方案8：购买康乃馨4支，购买兰花3支；（2）由题意，得，购花的方案有：
10、方案1：购买康乃馨1支，购买兰花6支；方案2：购买康乃馨1支，购买兰花7支；方案4：购买康乃馨2支，购买兰花5支；方案5：购买康乃馨2支，购买兰花6支；小明实现购买方案的愿望有5种，而总共有8中购买方案，小明能实现购买愿望的概率为P=考点三：设计销售方案问题在商品买卖中，更多蕴含着数学的学问。在形形色色的让利、打折、买一赠一、摸奖等促销活动中，大家不能被表象所迷惑，需要理智的分析。通过计算不同的销售方案盈利情况，可以帮助我们明白更多的道理。近来还出现运用概率统计知识进行设计的问题。例3四川省第十二届运动会将于2014年8月18日在我市隆重开幕，根据大会组委会安排，某校接受了开幕式大型团体操表演
11、任务为此，学校需要采购一批演出服装，A、B两家制衣公司都愿成为这批服装的供应商经了解：两家公司生产的这款演出服装的质量和单价都相同，即男装每套120元，女装每套100元经洽谈协商：A公司给出的优惠条件是，全部服装按单价打七折，但校方需承担2200元的运费；B公司的优惠条件是男女装均按每套100元打八折，公司承担运费另外根据大会组委会要求，参加演出的女生人数应是男生人数的2倍少100人，如果设参加演出的男生有x人（1）分别写出学校购买A、B两公司服装所付的总费用y1（元）和y2（元）与参演男生人数x之间的函数关系式；（2）问：该学校购买哪家制衣公司的服装比较合算？请说明理由思路分析：（1）根据总
12、费用=男生的人数男生每套的价格+女生的人数女生每套的价格就可以分别表示出y1（元）和y2（元）与男生人数x之间的函数关系式；（2）根据条件可以知道购买服装的费用受x的变化而变化，分情况讨论，当y1y2时，当y1=y2时，当y1y2时，求出x的范围就可以求出结论解：（1）总费用y1（元）和y2（元）与参演男生人数x之间的函数关系式分别是：y1=0.7120x+100（2x-100）+2200=224x-4800，y2=0.8100（3x-100）=240x-8000；（2）由题意，得当y1y2时，即224x-4800240x-8000，解得：x200当y1=y2时，即224x-4800=240x
13、-8000，解得：x=200当y1y2时，即224x-4800240x-8000，解得：x200即当参演男生少于200人时，购买B公司的服装比较合算；当参演男生等于200人时，购买两家公司的服装总费用相同，可任一家公司购买；当参演男生多于200人时，购买A公司的服装比较合算点评：本题考查了根据条件求一次函数的解析式的运用，运用不等式求设计方案的运用，解答本题时根据数量关系求出解析式是关键，建立不等式计算优惠方案是难点对应训练3为了迎接“十一”小长假的购物高峰某运动品牌专卖店准备购进甲、乙两种运动鞋其中甲、乙两种运动鞋的进价和售价如下表：运动鞋价格甲乙进价（元/双）mm-20售价（元/双）240
14、160已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同（1）求m的值；（2）要使购进的甲、乙两种运动鞋共200双的总利润（利润=售价-进价）不少于21700元，且不超过22300元，问该专卖店有几种进货方案？（3）在（2）的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠a（50a70）元出售，乙种运动鞋价格不变那么该专卖店要获得最大利润应如何进货？解：（1）依题意得，整理得，3000（m-20）=2400m，解得m=100，经检验，m=100是原分式方程的解，所以，m=100；（2）设购进甲种运动鞋x双，则乙种运动鞋（200-x）双，根据题
15、意得，解不等式得，x95，解不等式得，x105，所以，不等式组的解集是95x105，x是正整数，105-95+1=11，共有11种方案；（3）设总利润为W，则W=（140-a）x+80（200-x）=（60-a）x+16000（95x105），当50a60时，60-a0，W随x的增大而增大，所以，当x=105时，W有最大值，即此时应购进甲种运动鞋105双，购进乙种运动鞋95双；当a=60时，60-a=0，W=16000，（2）中所有方案获利都一样；当60a70时，60-a0，W随x的增大而减小，所以，当x=95时，W有最大值，即此时应购进甲种运动鞋95双，购进乙种运动鞋105双考点四：设计图案
16、问题图形的分割、拼接问题是考查动手操作能力与空间想能力的一类重要问题，在各地的中考试题中经常出现。这类问题大多具有一定的开放性，要求学生多角度、多层次的探索，以展示思维的灵活性、发散性、创新性。例4 下面给出的正多边形的边长都是20cm，请分别按下列要求设计一种剪拼方法（用虚线表示你的设计方案，把剪拼线段用粗黑实线，在图中标注出必要的符号和数据，并作简要说明（1）将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型，使它的表面积与原正方形面积相等；（2）将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型，使它的表面积与原正三角形的面积相等；（3）将图3中的正五边形纸片剪拼成一个底
17、面是正五边形的直五棱柱模型，使它的表面积与原正五边形的面积相等思路分析：（1）在正方形四个角上分别剪下一个边长为5的小正方形，拼成一个正方形作为直四棱柱的底面即可；（2）在正三角形的每一角上找出到顶点距离是5的点，然后作边的垂线，剪下后拼成一个正三角形，作为直三棱柱的一个底面即可；（3）在正五边形的每一角上找出到顶点距离是5的点，然后作边的垂线，剪下后拼成一个正五边形，作为直五棱柱的一个底面即可解：（1）如图1，沿黑线剪开，把剪下的四个小正方形拼成一个正方形，再沿虚线折叠即可；（2）如图，2，沿黑线剪开，把剪下的三部分拼成一个正三角形，再沿虚线折叠即可；（3）如图3，沿黑线剪开，把剪下的五部分
18、拼成一个正五边形，再沿虚线折叠即可点评：本题考查了图形的剪拼，解题的关键在于根据拼成棱柱的表面积与原图形的面积相等，从而判断出剪下的部分拼成的图形应该是棱柱的一个底面对应训练4如图，有一张一个角为30，最小边长为2的直角三角形纸片，沿图中所示的中位线剪开后，将两部分拼成一个四边形，所得四边形的周长是（）A8或2 B10或4+2 C10或2D8或4+2 4D四、中考演练1为了落实 “惠民政策”，某市今年计划开发建设A、B两种户型的“廉租房”共40套投入资金不超过200万元，又不低于198万元开发建设办公室预算：一套A型“廉租房”的造价为5.2万元，一套B型“廉租房”的造价为4.8万元（1）请问有
19、几种开发建设方案？（2）哪种建设方案投入资金最少？最少资金是多少万元？（3）在（2）的方案下，为了让更多的人享受到“惠民”政策，开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金每套A户型“廉租房”的造价降低0.7万元，每套B户型“廉租房”的造价降低0.3万元，将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”，如果同时建设A、B两种户型，请你直接写出再次开发建设的方案解：（1）设建设A型x套，则B型（40-x）套，根据题意得，解不等式得，x15，解不等式得，x20，所以，不等式组的解集是15x20，x为正整数，x=15、16、17、18、19、20，答：共有6种方案；（2
20、）设总投资W万元，建设A型x套，则B型（40-x）套，W=5.2x+4.8（40-x）=0.4x+192，0.40，W随x的增大而增大，当x=15时，W最小，此时W最小=0.415+192=198万元；（3）设再次建设A、B两种户型分别为a套、b套，则（5.2-0.7）a+（4.8-0.3）b=150.7+（40-15）0.3，整理得，a+b=4，a=1时，b=3，a=2时，b=2，a=3时，b=1，所以，再建设方案：A型住房1套，B型住房3套；A型住房2套，B型住房2套；A型住房3套，B型住房1套2. 如图，A、B两地之间有一座山，汽车原来从A地到B地经过C地沿折线ACB行驶，现开通隧道后，
21、汽车直接沿直线AB行驶已知AC=10千米，A=30，B=45则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果保留根号）解：过C作CDAB于D，在RtACD中，AC=10，A=30，DC=ACsin30=5，AD=ACcos30=5，在RtBCD中，B=45，BD=CD=5，BC=5，则用AC+BC-（AD+BD）=10+5-（5+5）=5+5-5（千米）答：汽车从A地到B地比原来少走（5+5-5）千米3地震后，政府为安置灾民，从某厂调拨了用于搭建板房的板材5600m2和铝材2210m，计划用这些材料在某安置点搭建甲、乙两种规格的板房共100间，若搭建一间甲型板房或一间乙型板房所需板材和
22、铝材的数量如下表所示：板房规格板材数量（m2）铝材数量（m）甲型4030乙型6020请你根据以上信息，设计出甲、乙两种板房的搭建方案解：设甲种板房搭建x间，则乙种板房搭建（100-x）间，根据题意得：，解得：20x21，x只能取整数，则x=20，21，共有2种搭建方案，方案1甲种板房搭建20间，乙种板房搭建80间，方案2甲种板房搭建21间，乙种板房搭建79间4某公司有甲种原料260kg，乙种原料270kg，计划用这两种原料生产A、B两种产品共40件生产每件A种产品需甲种原料8kg，乙种原料5kg，可获利润900元；生产每件B种产品需甲种原料4kg，乙种原料9kg，可获利润1100元设安排生产A
23、种产品x件（1）完成下表甲（kg）乙（kg）件数（件）A5xxB4（40-x）40-x（2）安排生产A、B两种产品的件数有几种方案？试说明理由；（3）设生产这批40件产品共可获利润y元，将y表示为x的函数，并求出最大利润解：（1）表格分别填入：A甲种原料8x，B乙种原料9（40-x）；（2）根据题意得，由得，x25，由得，x22.5，不等式组的解集是22.5x25，x是正整数，x=23、24、25，共有三种方案；方案一：A产品23件，B产品17件，方案二：A产品24件，B产品16件；方案三：A产品25件，B产品15件；（3）y=900x+1100（40-x）=-200x+44000，-2000
24、，y随x的增大而减小，x=23时，y有最大值，y最大=-20023+44000=39400元5地震给人民的生命财产带来巨大损失某市民政部门将租用甲、乙两种货车共16辆，把粮食266吨、副食品169吨全部运到灾区已知一辆甲种货车同时可装粮食18吨、副食品10吨；一辆乙种货车同时可装粮食16吨、副食11吨（1）若将这批货物一次性运到灾区，有哪几种租车方案？（2）若甲种货车每辆需付燃油费1500元；乙种货车每辆需付燃油费1200元，应选（1）中的哪种方案，才能使所付的费用最少？最少费用是多少元？解：（1）设租用甲种货车x辆，租用乙种货车为（16-x）辆，根据题意得，由得，x5，由得，x7，所以，5x
25、7，x为正整数，x=5或6或7，因此，有3种租车方案：方案一：组甲种货车5辆，乙种货车11辆；方案二：组甲种货车6辆，乙种货车10辆；方案三：组甲种货车7辆，乙种货车9辆；（2）方法一：由（1）知，租用甲种货车x辆，租用乙种货车为（16-x）辆，设两种货车燃油总费用为y元，由题意得，y=1500x+1200（16-x），=300x+19200，3000，当x=5时，y有最小值，y最小=3005+19200=20700元；方法二：当x=5时，16-5=11，51500+111200=20700元；当x=6时，16-6=10，61500+101200=21000元；当x=7时，16-7=9，715
26、00+91200=21300元；答：选择（1）中的方案一租车，才能使所付的费用最少，最少费用是20700元6如图，小明在楼上点A处测量大树的高，在A处测得大树顶部B的仰角为25，测得大树底部C的俯角为45已知点A距地面的高度AD为12m，求大树的高度BC（最后结果精确到0.1）解：过A作AEBC于E，则四边形ADCE是矩形，CE=AD=12m在RtACE中，EAC=45，AE=CE=12m，在RtAEB中，BAE=25，BE=AEtan25120.47=5.64mBC=BE+CE5.64+1217.6答：大树的高度约为17.6m点评：此题考查了仰角与俯角的知识此题难度适中，注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键
