1、2020年人教版八年级数学上册第12章 全等三角形单元测试卷一选择题（共10小题）1下列说法正确的是（）A全等三角形的三条边相等，三个角也相等B判定两个三角形全等的条件中至少有一个是等边C面积相等的两个图形是全等形D全等三角形的面积和周长都相等2下列说法正确的是（）A两个等边三角形一定全等B腰对应相等的两个等腰三角形全等C形状相同的两个三角形全等D全等三角形的面积一定相等3如图，点B、C分别在线段NM、NA上，在ABC中，A：ABC：BCA3：5：10，且ABCMNC，则BCM：NBA等于（）A1：2B1：3C1：4D1：54如图，RtABCRtDEF，E55，则A的度数为（）A25B35C4
2、5D555如图，下列条件中，不能证明ABDACD的是（）AABAC，BDCDBBC，BADCADCBC，BDCDDADBADC，DBDC6下列两个三角形中，一定全等的是（）A两个等腰三角形B两个等腰直角三角形C两个等边三角形D两个周长相等的等边三角形7如图，CDAB，BEAC，垂足分别为D、E，BE、CD相交于点O如果ABAC，那么图中全等的直角三角形的对数是（）A1B2C3D48下列条件中能说明两个直角三角形全等的是（）A锐角分别相等B一条直角边分别相等C斜边分别相等D两直角边分别相等9下列画图语句中正确的是（）A画射线OP5cmB画射线OA的反向延长线C画出A、B两点的中点D画出A、B两点
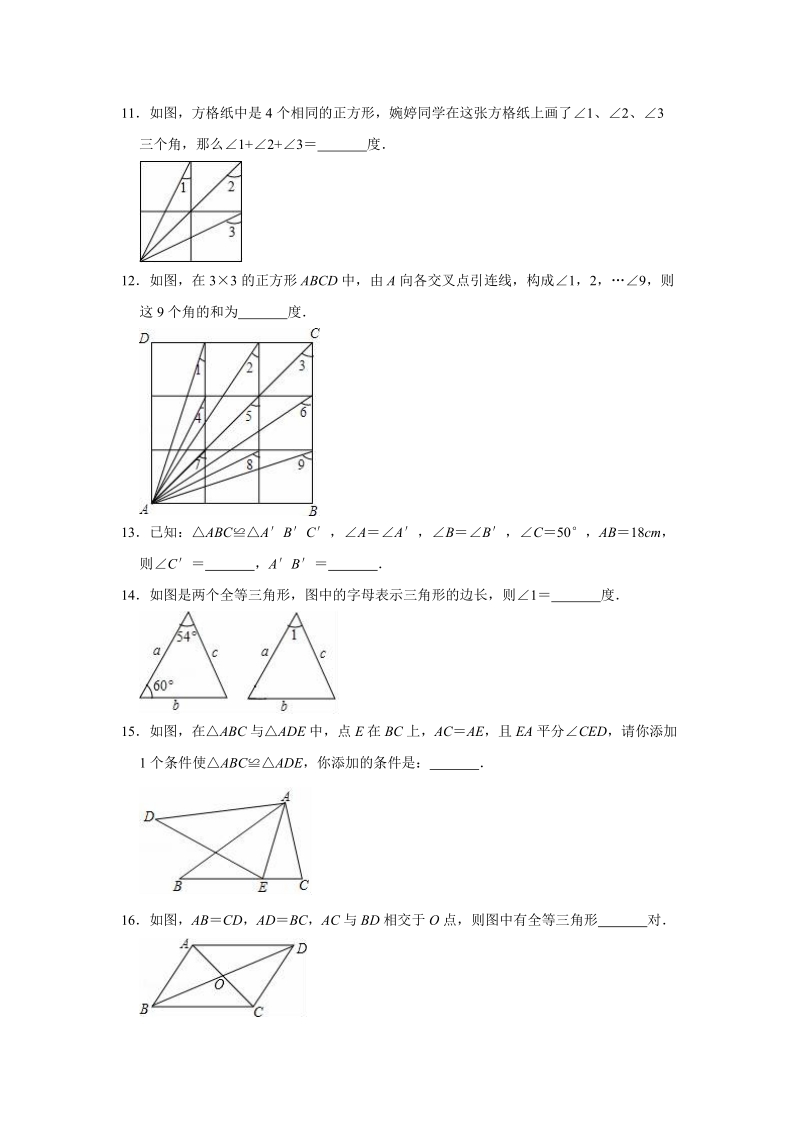
3、的距离10下列作图语句正确的是（）A作线段AB，使ABB延长线段AB到C，使ACBCC作AOB，使AOBD以O为圆心作弧二填空题（共8小题）11如图，方格纸中是4个相同的正方形，婉婷同学在这张方格纸上画了1、2、3三个角，那么1+2+3 度12如图，在33的正方形ABCD中，由A向各交叉点引连线，构成1，2，9，则这9个角的和为 度13已知：ABCABC，AA，BB，C50，AB18cm，则C ，AB 14如图是两个全等三角形，图中的字母表示三角形的边长，则1 度15如图，在ABC与ADE中，点E在BC上，ACAE，且EA平分CED，请你添加1个条件使ABCADE，你添加的条件是： 16如图，
4、ABCD，ADBC，AC与BD相交于O点，则图中有全等三角形 对17如图，在RtABC和RtDCB中，ABDC，AD90，AC与BD交于点O，则有 ，其判定依据是 ，还有 ，其判定依据是 18在RtABC和RtDEF中，ABDE，AD90，再补充一个条件 ，便可得RtABCRtDEF三解答题（共8小题）19如图，ACFDBE，其中点A、B、C、D在一条直线上（1）若BEAD，F62，求A的大小；（2）若AD9cm，BC5cm，求AB的长20如图1，ABC与DBC全等，且ACBDBC90，AB6，AC4如图2，将DBC沿射线BC方向平移得到D1B1C1，连接AC1，BD1（1）求证：BD1AC1
5、且BD1AC1；（2）DBC沿射线BC方向平移的距离等于 时，点A与点D1之间的距离最小21已知：如图，点E、F在线段BD上，BEDF，ABCD，AC求证：ABFCDE22已知，如图，ABAE，ABDE，ECB70，D110，求证：ABCEAD23如图，已知AB，OAOB，AD与BC相交于点E，试证明：（1）OADOBC；（2）AEBE24如图，在ABC和ABD中，BACABD90，点E为AD边上的一点，且ACAE，连接CE交AB于点G，过点A作AFAD交CE于点F（1）求证：AGEAFC；（2）若ABAC，求证：ADAF+BD25如图，有一湖的湖岸在A、B之间呈一段圆弧状，A、B间的距离不能
6、直接测得你能用已学过的知识或方法设计测量方案，求出A、B间的距离吗？26如图，A、B两建筑物位于河的两岸，要测得它们之间的距离，可以从B点出发沿河岸画一条射线BF，在BF上截取BCCD，过D作DEAB，使E、C、A在同一直线上，则DE的长就是A、B之间的距离，请你说明道理2020年人教版八年级数学上册第12章 全等三角形单元测试卷参考答案与试题解析一选择题（共10小题）1下列说法正确的是（）A全等三角形的三条边相等，三个角也相等B判定两个三角形全等的条件中至少有一个是等边C面积相等的两个图形是全等形D全等三角形的面积和周长都相等【分析】根据全等形的概念和性质进行解答，注意全等中的对应不能忽略【
7、解答】解：全等三角形的三条对应边相等，三个对应角也相等，A不正确；判定两个三角形全等的条件中至少有一个是等边，B正确；面积相等的两个图形不一定是全等形，C不正确；全等三角形的面积和周长都相等，D正确，故选：BD【点评】本题考查的是全等形的性质，能够完全重合的两个图形叫做全等形，全等形的对应边相等，对应角也相等，面积和周长都相等2下列说法正确的是（）A两个等边三角形一定全等B腰对应相等的两个等腰三角形全等C形状相同的两个三角形全等D全等三角形的面积一定相等【分析】根据全等图形的判定和性质对各个选项进行判断即可【解答】解：两个等边三角形边长不一定相等，所以不一定全等，A错误；腰对应相等的两个等腰三
8、角形对应角不一定相等，所以不一定全等，B错误；形状相同的两个三角形对应边不一定相等，所以不一定全等，C错误；全等三角形的面积一定相等，所以D正确，故选：D【点评】本题考查的是全等图形的判定和性质，对应角相等、对应边相等的两个图形确定，全等形的周长和面积相等3如图，点B、C分别在线段NM、NA上，在ABC中，A：ABC：BCA3：5：10，且ABCMNC，则BCM：NBA等于（）A1：2B1：3C1：4D1：5【分析】由三角形内角和定理求出A、ABC、ACB的度数，由全等三角形的性质、三角形的外角性质、等腰三角形的性质求出BCM和NBA的度数，即可得出答案【解答】解：A：ABC：ACB3：5：1
9、0，A+ABC+ACB180，A30，ABC50，ACB100，MNCABC，NABC50，MA30，CNBC，MCAM+N80，CBNN50，BCMACBMCA20，NBACBN+ABC50+50100，BCM：NBA1：5，故选：D【点评】本题考查的是全等三角形的性质、等腰三角形的性质以及三角形的外角性质，掌握全等三角形的对应角相等是解题的关键4如图，RtABCRtDEF，E55，则A的度数为（）A25B35C45D55【分析】根据三角形内角和定理求出EDF，根据全等三角形的性质解答【解答】解：EFD90，E55，EDF905535，RtABCRtDEF，AEDF35，故选：B【点评】本题
10、考查的是全等三角形的性质，三角形内角和定理，掌握全等三角形的对应角相等是解题的关键5如图，下列条件中，不能证明ABDACD的是（）AABAC，BDCDBBC，BADCADCBC，BDCDDADBADC，DBDC【分析】根据公共边AD和各选项中给出的条件分别证明ABDACD即可解题【解答】解：A、在ABD和ACD中，ABDACD；（SSS）；故A正确；B、在ABD和ACD中，ABDACD；（AAS）；故A正确；C、在ABD和ACD中，ASS不能证明三角形全等，故C错误；D、在ABD和ACD中，ABDACD；（SAS）；故D正确；故选：C【点评】本题考查了SSS，AAS，SAS证明三角形全等的方法
11、，本题中牢记ASS不能求证三角形全等是解题的关键6下列两个三角形中，一定全等的是（）A两个等腰三角形B两个等腰直角三角形C两个等边三角形D两个周长相等的等边三角形【分析】由全等三角形的判定方法得出A、B、C不正确，D正确，即可得出结论【解答】解：两个等腰三角形不一定全等，选项A不正确；两个等腰直角三角形一定相似，不一定全等，选项B不正确；两个等边三角形一定相似，不一定全等，选项C不正确；两个周长相等的等边三角形的边长相等，两个周长相等的等边三角形一定全等，选项D正确；故选：D【点评】本题考查了全等三角形的判定方法、等边三角形的性质、等腰直角三角形的性质、等腰三角形的性质；熟记全等三角形的判定方
12、法是解决问题的关键7如图，CDAB，BEAC，垂足分别为D、E，BE、CD相交于点O如果ABAC，那么图中全等的直角三角形的对数是（）A1B2C3D4【分析】共有4对分别为ADCAEB，BODCOERtADORtAEO，ABOACO；做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找【解答】解：CDAB，BEAC，ADCAEE90，在ADC和AEB中，ADCAEB（AAS）；ADAE，CB，ABAC，BDCE，在BOD和COE中，BODCOE（AAS）；OBOC，ODOE，在RtADO和RtAEO中，RtADORtAEO（HL）；在ABO和ACO中，ABOACO（SSS）共有4对
13、全等三角形故选：D【点评】本题考查三角形全等的判定方法，熟练掌握全等三角形的判定方法是解题的关键8下列条件中能说明两个直角三角形全等的是（）A锐角分别相等B一条直角边分别相等C斜边分别相等D两直角边分别相等【分析】依据全等三角形的判定定理进行判断即可【解答】解：A、没有边对应相等，不一定全等，B、一条直角边和一组直角相等，不一定全等；C、一组斜边和一组直角相等，不一定全等；D、两直角边分别相等，依据SAS可证明两个三角形全等故选：D【点评】本题主要考查的是全等三角形的判定，熟练掌握全等三角形的判定定理是解题的关键9下列画图语句中正确的是（）A画射线OP5cmB画射线OA的反向延长线C画出A、B
14、两点的中点D画出A、B两点的距离【分析】利用射线的定义，线段中点及距离的定义判定即可【解答】解：A、画射线OP5cm，错误，射线没有长度，B、画射线OA的反向延长线，正确C、画出A、B两点的中点，错误，中点是线段的不是两点的，D、画出A、B两点的距离，错误，画出的是线段不是距离故选：B【点评】本题主要考查了射线及线段的中点，距离，解题的关键是熟记射线的定义，线段中点及距离的定义10下列作图语句正确的是（）A作线段AB，使ABB延长线段AB到C，使ACBCC作AOB，使AOBD以O为圆心作弧【分析】根据基本作图的方法，逐项分析，从而得出正确的结论【解答】解：A、应为：作线段AB，使AB，故本选项
15、错误；B、应为：延长线段AB到C，BCAB，故本选项错误；C、作AOB，使AOB，故本选项正确；D、需要说明半径的长，故选项错误故选：C【点评】本题考查尺规作图的定义：只能用没有刻度的直尺和圆规二填空题（共8小题）11如图，方格纸中是4个相同的正方形，婉婷同学在这张方格纸上画了1、2、3三个角，那么1+2+3135度【分析】根据ABCEDC得到3BAC，求出1+390，根据等腰直角三角形的性质得到245，计算即可【解答】解：由题意可知ABCEDC，3BAC，又1+BAC90，1+390，DFDC，245，1+2+3135度，故答案为：135【点评】本题考查的是全等三角形的判定和性质、等腰直角三
16、角形的性质，根据题意和图形证明ABCEDC是解题的关键12如图，在33的正方形ABCD中，由A向各交叉点引连线，构成1，2，9，则这9个角的和为405度【分析】根据题意和全等三角形的判定定理找出全等三角形，根据全等三角形的性质计算即可得到答案【解答】解：观察图形可知：1所在的三角形与9所在的三角形全等，1与9的余角相等，也就是1与9互余，同理：2与6互余4与8互余，又357451+990、2+690、4+890、3+790、545，1+2+3+9405故答案为：405【点评】考查三角形全等的性质的运用：由三角形全等得到对应角角相等认真观察图形，发现并利用全等三角形是正确解决本题的关键13已知：
17、ABCABC，AA，BB，C50，AB18cm，则C50，AB18cm【分析】根据全等三角形的对应边相等、对应角相等解答【解答】解：ABCABC，C50，AB18cm，CC50，ABAB18cm，故答案为：50；18cm【点评】本题考查的是全等三角形的性质，掌握全等三角形的对应边相等、对应角相等是解题的关键14如图是两个全等三角形，图中的字母表示三角形的边长，则154度【分析】根据全等三角形的对应角相等解答【解答】解：两个三角形全等，154，故答案为：54【点评】本题考查的是全等三角形的性质，掌握全等三角形的对应角相等是解题的关键15如图，在ABC与ADE中，点E在BC上，ACAE，且EA平分
18、CED，请你添加1个条件使ABCADE，你添加的条件是：BD【分析】根据角平分线的定义、等腰三角形的性质得到AEDC，利用AAS定理证明ABCADE【解答】解：添加BD或BCDE或BACDAE或BADEAC（答案不唯一），EA平分CED，AEDAEC，ACAE，CAEC，AEDC，当BD时，在ABC和ADE中，ABCADE（AAS），故答案为：BD【点评】本题考查的是全等三角形的判定，掌握角平分线的定义、等腰三角形的性质、全等三角形的判定定理是解题的关键16如图，ABCD，ADBC，AC与BD相交于O点，则图中有全等三角形4对【分析】利用全等三角形的判定及性质做题，做题时，从已知开始结合全等的
19、判定方法由易到难逐个找寻，要不重不漏【解答】解：ABCD，ADBC，又BDDB，ABDCDB，进而可得ADCABC，AODBOC，ABOCDO，共4对故答案为4【点评】本题考查了全等三角形的判定；做题时注意由易到难进行，这是比较关键的17如图，在RtABC和RtDCB中，ABDC，AD90，AC与BD交于点O，则有ABCDCB，其判定依据是HL，还有ABODCO，其判定依据是AAS【分析】根据已知条件，利用HL可直接判定ABCDCB，然后利用全等三角形的对应边相等，根据AAS可判定ABODCO【解答】解：在RtABC和RtDCB中，ABDC，AD90，BC是RtABC和RtDCB的公共边，根据
20、HL，ABCDCB；由ABCDCB（已证）得ABDC，在ABO 和DCO 中，AD90，AOBDOC（对顶角），依据是AAS可判定ABODCO故答案为：ABD；DCB；HL；ABO；DCO【点评】此题主要考查学生对全等三角形判定这一知识点的理解和掌握，解答此题的关键是先利用HL求证ABCDCB，然后利用全等三角形对应边相等，利用AAS来求证ABODCO 的18在RtABC和RtDEF中，ABDE，AD90，再补充一个条件答案不唯一，如BCEF等，便可得RtABCRtDEF【分析】由直角三角形全等的判定方法HL，即可得出结论【解答】解：补充一个条件BCEF，便可得RtABCRtDEF；理由如下：
21、在RtABC和RtDEF中，RtABCRtDEF（HL）【点评】本题考查了直角三角形全等的判定方法；熟练掌握直角三角形全等的判定方法是解决问题的关键三解答题（共8小题）19如图，ACFDBE，其中点A、B、C、D在一条直线上（1）若BEAD，F62，求A的大小；（2）若AD9cm，BC5cm，求AB的长【分析】（1）根据全等三角形的性质得到FCAEBD90，根据直角三角形的性质计算即可；（2）根据全等三角形的性质得到CABD，结合图形得到ABCD，计算即可【解答】解：（1）BEAD，EBD90，ACFDBE，FCAEBD90，A90F28；（2）ACFDBE，CABD，CACBBDBC，即AB
22、CD，AD9cm，BC5cm，AB+CD954cm，AB2cm【点评】本题考查的是全等三角形的性质，掌握全等三角形的对应边相等、对应角相等是解题的关键20如图1，ABC与DBC全等，且ACBDBC90，AB6，AC4如图2，将DBC沿射线BC方向平移得到D1B1C1，连接AC1，BD1（1）求证：BD1AC1且BD1AC1；（2）DBC沿射线BC方向平移的距离等于2时，点A与点D1之间的距离最小【分析】（1）根据全等三角形的性质、平移的性质得到四边形BD1C1A为平行四边形，根据平行四边形的性质证明结论；（2）根据勾股定理计算即可【解答】（1）证明：由图1可知，ACBDBC，ABCD，ACBD
23、，ABCDCB，ABCD，由平移的性质可知，CDC1D，CDC1D，ABC1D，ABC1D，四边形BD1C1A为平行四边形，BD1AC1且BD1AC1；（2）解：当点C于点B重合时，点A与点D1之间的距离最小，DBC沿射线BC方向平移的距离BC2，故答案为：2【点评】本题考查的是全等三角形的性质、平移的性质、平行四边形的判定和性质，掌握全等三角形的性质定理、平移的性质是解题的关键21已知：如图，点E、F在线段BD上，BEDF，ABCD，AC求证：ABFCDE【分析】两角及其中一个角的对边对应相等的两个三角形全等，据此利用AAS进行判定即可【解答】证明：BEDF，BE+EFDF+EF，即BFDE
24、，ABCD，BD，在ABF和CDE中，ABFCDE（AAS）【点评】此题考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解本题的关键22已知，如图，ABAE，ABDE，ECB70，D110，求证：ABCEAD【分析】由ECB70得ACB110，再由ABDE，证得CABE，再结合已知条件ABAE，可利用AAS证得ABCEAD【解答】证明：由ECB70得ACB110又D110ACBDABDECABE在ABC和EAD中ABCEAD（AAS）【点评】本题是全等三角形证明的基础题型，在有些条件还需要证明时，应先把它们证出来，再把条件用大括号列出来，根据等三角形证明的方法判定即可23如图，已知AB，
25、OAOB，AD与BC相交于点E，试证明：（1）OADOBC；（2）AEBE【分析】（1）根据ASA证明OADOBC；（2）可通过证明ACEBDE获得【解答】解：（1）在OAD和OBC中，OADOBC（ASA）（2）由（1）得OADOBCOCOD，OAOCOBOD，即ACBD在ACE和BDE中，ACEBDE（AAS），AEBE【点评】本题考查了全等三角形的判定和性质学会分析是关键全等三角形的判定条件有四种：SSS，SAS，ASA，AAS24如图，在ABC和ABD中，BACABD90，点E为AD边上的一点，且ACAE，连接CE交AB于点G，过点A作AFAD交CE于点F（1）求证：AGEAFC；（2
26、）若ABAC，求证：ADAF+BD【分析】（1）根据等腰三角形的性质得到CAEG，利用ASA定理证明AGEAFC；（2）延长AF至点H，使AHAD，证明CAHBAD，根据全等三角形的性质得到CHBD，ACHABD90，得到CHAB，证明HCHF，结合图形证明结论【解答】证明：（1）CABFAE90，CABFAGFAEFAG，即CAFEAG，ACAE，ACFAEG，在AGE和AFC中，AGEAFC（ASA）；（2）延长AF至点H，使AHAD，在CAH和BAD中，CAHBAD（SAS）CHBD，ACHABD90，CHAB，CHAHAG，AGEAFC，AGEAFC，AGFAFG，HCFHFC，HCH
27、F，AHAF+HFAF+CH，ADAF+BD【点评】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键25如图，有一湖的湖岸在A、B之间呈一段圆弧状，A、B间的距离不能直接测得你能用已学过的知识或方法设计测量方案，求出A、B间的距离吗？【分析】过点B作AB的垂线BF，在BF上取两点C、D，使CDBC，再定出BF的垂线DE，使A、C、E在一条直线上，可证EDCABC，即可证明DEBA【解答】解：要测量A、B间的距离，可用如下方法：过点B作AB的垂线BF，在BF上取两点C、D，使CDBC，再作出BF的垂线DE，使A、C、E在一条直线上，ACBECD，CBCD，ABC
28、EDC，EDCABC（ASA）DEBA答：测出DE的长就是A、B之间的距离【点评】本题考查了全等三角形在实际生活中的应用，全等三角形的证明，全等三角形对应边相等的性质，本题中求证EDCABC是解题的关键26如图，A、B两建筑物位于河的两岸，要测得它们之间的距离，可以从B点出发沿河岸画一条射线BF，在BF上截取BCCD，过D作DEAB，使E、C、A在同一直线上，则DE的长就是A、B之间的距离，请你说明道理【分析】根据BCCD，CEDCAB，ACBECD，即可求证ABCEDC，根据全等三角形对应边相等的性质可以求得ABDE【解答】解：DEAB，CEDCAB，ABCEDC（AAS），ABED，答：DE的长就是A、B之间的距离【点评】本题考查了全等三角形在实际生活中的应用，考查了全等三角形的证明和对应边相等的性质，本题中正确的求证ABCEDC是解题的关键
