1、章末检测一、选择题1.观察图中四个几何体，其中判断正确的是()A.(1)是棱台B.(2)是圆台C.(3)是棱锥D.(4)不是棱柱答案C解析结合柱、锥、台、球的定义可知(3)是棱锥，(4)是棱柱，故选C.2.如图，OAB是水平放置的OAB的直观图，则OAB的面积为()A.6B.3C.6D.12答案D解析由斜二测画法规则可知，OAB为直角三角形，且两直角边长分别为4和6，故面积为12.3.设m，n是两条不同的直线，是两个不同的平面()A.若m，n，则mnB.若m，m，则C.若mn，m，则nD.若m，则m答案C解析A项，当m，n时，m，n可能平行，可能相交，也可能异面，故错误；B项，当m，m时，可能
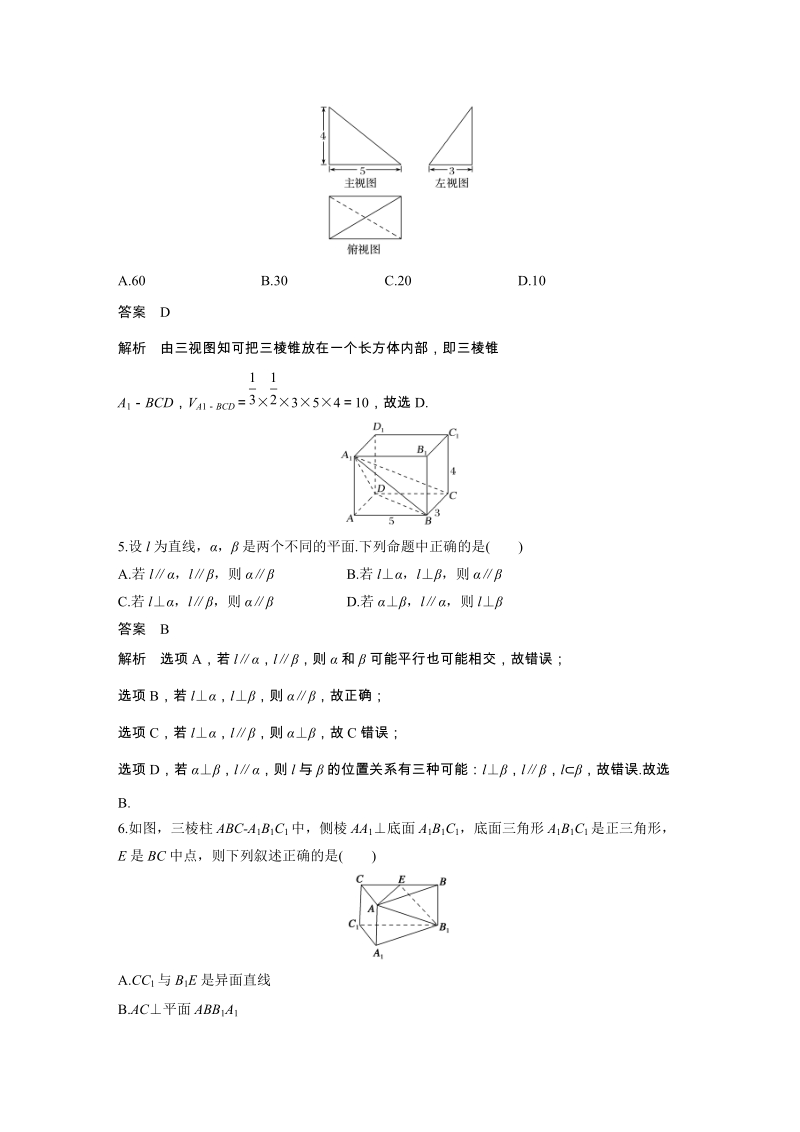
2、平行也可能相交，故错误；C项，当mn，m时，n，故正确；D项，当m，时，m可能与平行，可能在内，也可能与相交，故错误.故选C.4.某三棱锥的三视图如图所示，则该三棱锥的体积为()A.60 B.30 C.20 D.10答案D解析由三视图知可把三棱锥放在一个长方体内部，即三棱锥A1BCD，VA1BCD35410，故选D.5.设l为直线，是两个不同的平面.下列命题中正确的是()A.若l，l，则B.若l，l，则C.若l，l，则D.若，l，则l答案B解析选项A，若l，l，则和可能平行也可能相交，故错误；选项B，若l，l，则，故正确；选项C，若l，l，则，故C错误；选项D，若，l，则l与的位置关系有三种可
3、能：l，l，l，故错误.故选B.6.如图，三棱柱ABC-A1B1C1中，侧棱AA1底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC中点，则下列叙述正确的是()A.CC1与B1E是异面直线B.AC平面ABB1A1C.AE，B1C1为异面直线，且AEB1C1D.A1C1平面AB1E答案C解析由已知ACAB，E为BC中点，故AEBC，又BCB1C1，AEB1C1，C正确.7.已知m，n为异面直线，m平面，n平面.直线l满足lm，ln，l，l，则()A.且lB.且lC.与相交，且交线垂直于lD.与相交，且交线平行于l答案D解析根据所给的已知条件作图，如图所示.由图可知与相交，且交线平行于l
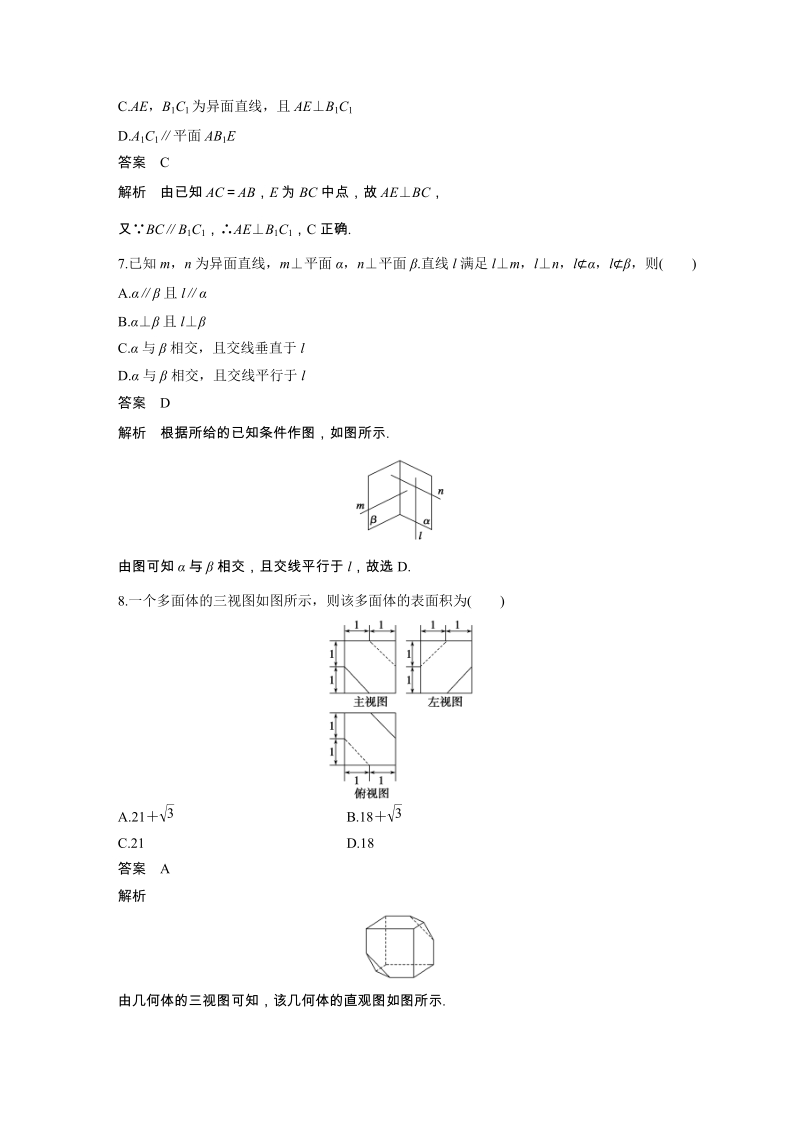
4、，故选D.8.一个多面体的三视图如图所示，则该多面体的表面积为()A.21B.18C.21D.18答案A解析由几何体的三视图可知，该几何体的直观图如图所示.因此该几何体的表面积为6(4)2()221.故选A.9.如图，在四边形ABCD中，ADBC，ADAB，BCD45，BAD90，将ABD沿BD折起，使平面ABD平面BCD，构成三棱锥ABCD，则在三棱锥ABCD中，下列命题正确的是()A.平面ABD平面ABCB.平面ADC平面BDCC.平面ABC平面BDCD.平面ADC平面ABC答案D解析如图，在平面图形中CDBD，折起后仍然满足CDBD，由于平面ABD平面BCD，故CD平面ABD，CDAB.
5、又ABAD，故AB平面ADC，又AB平面ABC，所以平面ADC平面ABC.10.已知三棱锥S-ABC的所有顶点都在球O的球面上，ABC是边长为1的正三角形，SC为球O的直径，且SC2，则此棱锥的体积为()A.B.C.D.答案A解析利用三棱锥的体积变换求解.由于三棱锥S-ABC与三棱锥O-ABC底面都是ABC，O是SC的中点，因此三棱锥S-ABC的高是三棱锥O-ABC高的2倍，所以三棱锥S-ABC的体积也是三棱锥O-ABC体积的2倍.在三棱锥O-ABC中，其棱长都是1，如图所示，SABCAB2，高OD，VS-ABC2VO-ABC2.二、填空题11.设平面平面，A、C，B、D，直线AB与CD交于点
6、S，且点S位于平面，之间，AS8，BS6，CS12，则SD_.答案9解析由面面平行的性质得ACBD，解得SD9.12.如图所示，在正方体ABCDA1B1C1D1中，M，N分别是棱AA1和AB上的点，若B1MN是直角，则C1MN等于_.答案90解析B1C1平面A1ABB1，MN平面A1ABB1，B1C1MN，又B1MN为直角.B1MMN，而B1MB1C1B1.MN平面MB1C1又MC1平面MB1C1，MNMC1，C1MN90.13.如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下面及母线均相切.记圆柱O1O2的体积为V1，球O的体积为V2，则的值是_.答案解析设球半径为R，则圆柱底面圆半径为
7、R，母线长为2R，又V1R22R2R3，V2R3，所以.14.下列四个命题：若ab，a，则b；若a，b，则ab；若a，则a平行于内所有的直线；若a，ab，b，则b.其中正确命题的序号是_.答案解析中b可能在内；a与b可能异面；a可能与内的直线异面.三、解答题15.如图，三棱柱ABC-A1B1C1的侧棱与底面垂直，AC9，BC12，AB15，AA112，点D是AB的中点.(1)求证：ACB1C；(2)求证：AC1平面CDB1.证明(1)C1C平面ABC，C1CAC.AC9，BC12，AB15，AC2BC2AB2，ACBC.又BCC1CC，AC平面BCC1B1，而B1C平面BCC1B1，ACB1C
8、.(2)连接BC1交B1C于O点，连接OD.如图，O，D分别为BC1，AB的中点，ODAC1.又OD平面CDB1，AC1平面CDB1.AC1平面CDB1.16.由四棱柱ABCDA1B1C1D1截去三棱锥C1B1CD1后得到的几何体如图所示.四边形ABCD为正方形，O为AC与BD的交点，E为AD的中点，A1E平面ABCD.(1)证明：A1O平面B1CD1；(2)设M是OD的中点，证明：平面A1EM平面B1CD1.证明(1)取B1D1的中点O1，连接CO1，A1O1，由于ABCDA1B1C1D1是四棱柱，所以A1O1OC，A1O1OC，因此四边形A1OCO1为平行四边形，所以A1OO1C，又O1C
9、平面B1CD1，A1O平面B1CD1，所以A1O平面B1CD1.(2)因为ACBD，E，M分别为AD和OD的中点，所以EMBD，又A1E平面ABCD，BD平面ABCD，所以A1EBD，因为B1D1BD，所以EMB1D1，A1EB1D1，又A1E，EM平面A1EM，A1EEME，所以B1D1平面A1EM，又B1D1平面B1CD1，所以平面A1EM平面B1CD1.17.如图，在三棱锥PABC中，PAAB，PABC，ABBC，PAABBC2，D为线段AC的中点，E为线段PC上一点. (1)求证：PABD；(2)求证：平面BDE平面PAC；(3)当PA平面BDE时，求三棱锥EBCD的体积.(1)证明P
10、AAB，PABC，AB平面ABC，BC平面ABC，且ABBCB，PA平面ABC，又BD平面ABC，PABD.(2)证明ABBC，D是AC的中点，BDAC.由(1)知PA平面ABC，PA平面PAC，平面PAC平面ABC.平面PAC平面ABCAC，BD平面ABC，BDAC，BD平面PAC.BD平面BDE，平面BDE平面PAC，(3)解PA平面BDE，又平面BDE平面PACDE，PA平面PAC，PADE.由(1)知PA平面ABC，DE平面ABC.D是AC的中点，E为PC的中点，DEPA1.D是AC的中点，SBCDSABC221，VEBCDSBCDDE11.18.如图(1)，在RtABC中，C90，D
11、，E分别为AC，AB的中点，点F为线段CD上的一点，将ADE沿DE折起到A1DE的位置，使A1FCD，如图(2).(1)求证：DE平面A1CB；(2)求证：A1FBE；(3)线段A1B上是否存在点Q，使A1C平面DEQ？说明理由.(1)证明D，E分别为AC，AB的中点，DEBC.又DE平面A1CB，DE平面A1CB.(2)证明由已知得ACBC且DEBC，DEAC.DEA1D，DECD.DE平面A1DC.而A1F平面A1DC，DEA1F.又A1FCD，DECDD，A1F平面BCDE，A1FBE.(3)解线段A1B上存在点Q，使A1C平面DEQ.理由如下：如图，分别取A1C，A1B的中点P，Q，则PQBC.又DEBC，DEPQ.平面DEQ即为平面DEP.由(2)知，DE平面A1DC，DEA1C.又P是等腰三角形DA1C底边A1C的中点，A1CDP.又DEDP=D，A1C平面DEP.从而A1C平面DEQ.故线段A1B上存在点Q(中点)，使得A1C平面DEQ.
