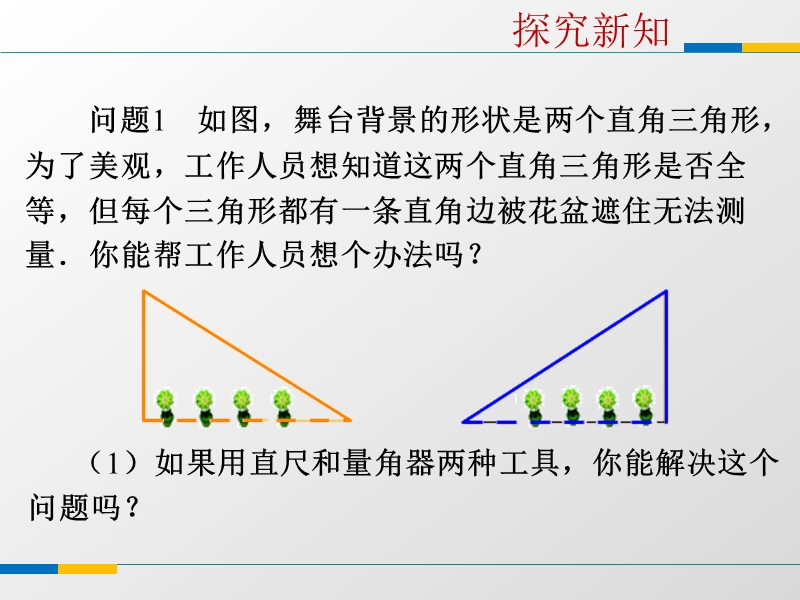
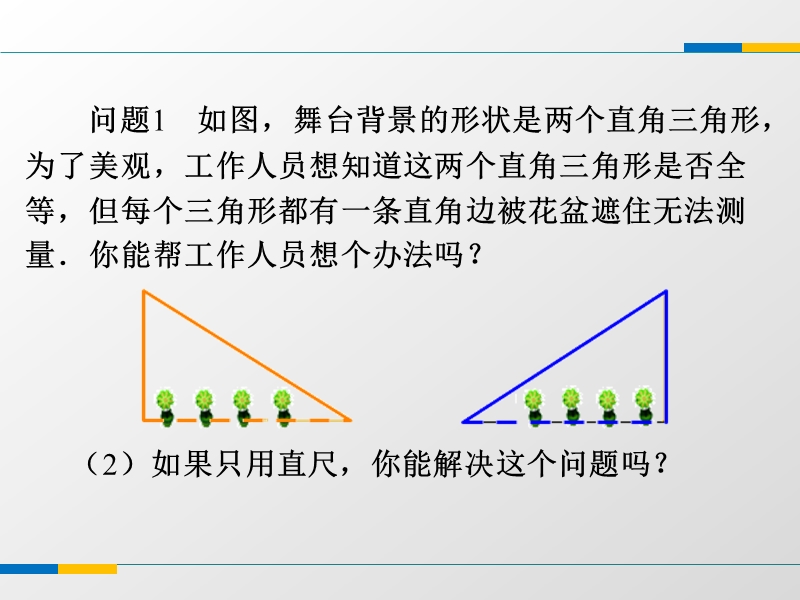
1、2.8 直角三角形全等的判定,问题1 如图，舞台背景的形状是两个直角三角形， 为了美观，工作人员想知道这两个直角三角形是否全 等，但每个三角形都有一条直角边被花盆遮住无法测 量你能帮工作人员想个办法吗？,（1）如果用直尺和量角器两种工具，你能解决这个 问题吗？,探究新知,（2）如果只用直尺，你能解决这个问题吗？,问题1 如图，舞台背景的形状是两个直角三角形， 为了美观，工作人员想知道这两个直角三角形是否全 等，但每个三角形都有一条直角边被花盆遮住无法测 量你能帮工作人员想个办法吗？,问题2 任意画一个RtABC，使C =90，再画 一个RtABC，使C=90，BC=BC， AB=AB，然后把画
2、好的RtABC剪下来放到 RtABC上，你发现了什么？,RtABC RtABC,（1） 画MCN =90； （2）在射线CM上取BC=BC； （3） 以B为圆心，AB为半径画弧，交射线C N于点A； （4）连接AB,现象：两个直角三角形能重合说明：这两个直角三角形全等,画法：,实验探索,斜边和一条直角边分别相等的两个直角三角形全等 （简写为“斜边、直角边”或“HL”）,几何语言： 在RtABC 和 RtABC中， AB =AB，BC =BC， RtABC RtABC（HL） ,探究归纳,证明： ACBC，BDAD， C 和D 都是直角 在RtABC 和 RtBAD 中，AB =BA，AC =B
3、D， RtABC RtBAD（HL） BC =AD（全等三角形对应边相等）,例1 如图，ACBC，BDAD，AC =BD求证：BC =AD,学以致用,变式1 如图，ACBC，BDAD，要证ABC BAD，需要添加一个什么条件？请说明理由 （1） （ ）； （2） （ ）； （3） （ ）； （4） （ ）,AD = BC,AC = BD,DAB = CBA,DBA = CAB,HL,HL,AAS,AAS,变式训练,问题3 如图，要在S 区建一个广告牌P，使它到 两条高速公路的距离相等，离两条公路交叉处500 m， 请你帮忙设计一下，这个广告牌P 应建于何处（在图上 标出它的位置，比例尺为1：2
4、0 000）？,继续探究,问题4 交换角的平分线的性质中的已知和结论， 你能得到什么结论，这个新结论正确吗？,在一个角的内部, 且到角的两边距离相等的点在这个角的平分线上.,如图, PD=PE, PDOA, PEOB,垂足分别是D, E(已知), 点P在AOB的平分线上. (在一个角的内部,且到角的两边距离相等的点在这个角的平分线上).,这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.,角的内部到角的两边距离相等的点在角的平分线上,探究归纳,已知: 如图所示, PD=PE, PDOA,PEOB, 垂足分别是D,E. 求证: 点P在AOB的平分线上.,证明： PDOA ，PEO
5、B POD和POE都是Rt PD=PE,OP=OP RtPODRtPOE(HL) POD= POE OC是AOB的平分线 点P在AOB的平分线上,探索证明,例2 如图, ABC的角平分线BM, CN相交于点P, 求证：点P到三边AB、BC、CA 的距离相等.,证明：过点P作PDAB于D，PEBC于E，PFAC于F BM为ABC的角平分线 PD=PE 同理, PE=PF. PDPE=PF 即点P到三边AB、BC、CA的距离相等,学以致用,X,1判断题：（1）如图，若QM =QN，则OQ 平分AOB；( ),课堂练习,X,1判断题：（2）如图，若QMOA 于M，QNOB 于N，则OQ是AOB 的平
6、分线； ( ),1判断题：（3）已知：Q 到OA 的距离等于2 cm， 且Q 到OB 距离等于2 cm，则Q 在AOB 的平分线上( ),2. 如图，有两个长度相同的滑梯，左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，两个滑梯 的倾斜角ABC 和DFE 的大小有什么关系？为什么？,ABC +DFE =90,证明： ACAB，DEDF， CAB 和FDE 都是直角 在RtABC 和 RtDEF 中，, RtABC RtDEF（HL）,2. 如图，有两个长度相同的滑梯，左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，两个滑梯 的倾斜角ABC 和DFE 的大小有什么关系？为什么？,证明： ABC =DEF （全等三角形对应角相等） DEF +DFE =90， ABC +DFE =90,2. 如图，有两个长度相同的滑梯，左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，两个滑梯 的倾斜角ABC 和DFE 的大小有什么关系？为什么？,（1）“HL”判定方法应满足什么条件？与之前所学的四种判定方法有什么不同？ （2）判定两个直角三角形全等有哪些方法？,课堂小结,（3）角平分线的性质定理的掌握与应用,教科书作业题第2、3、4题,课后作业,
