 2019-2020学年北京市海淀区清华大学附中九年级(上)开学数学试卷(解析版)
2019-2020学年北京市海淀区清华大学附中九年级(上)开学数学试卷(解析版)
《2019-2020学年北京市海淀区清华大学附中九年级(上)开学数学试卷(解析版)》由会员分享,可在线阅读,更多相关《2019-2020学年北京市海淀区清华大学附中九年级(上)开学数学试卷(解析版)(33页珍藏版)》请在七七文库上搜索。
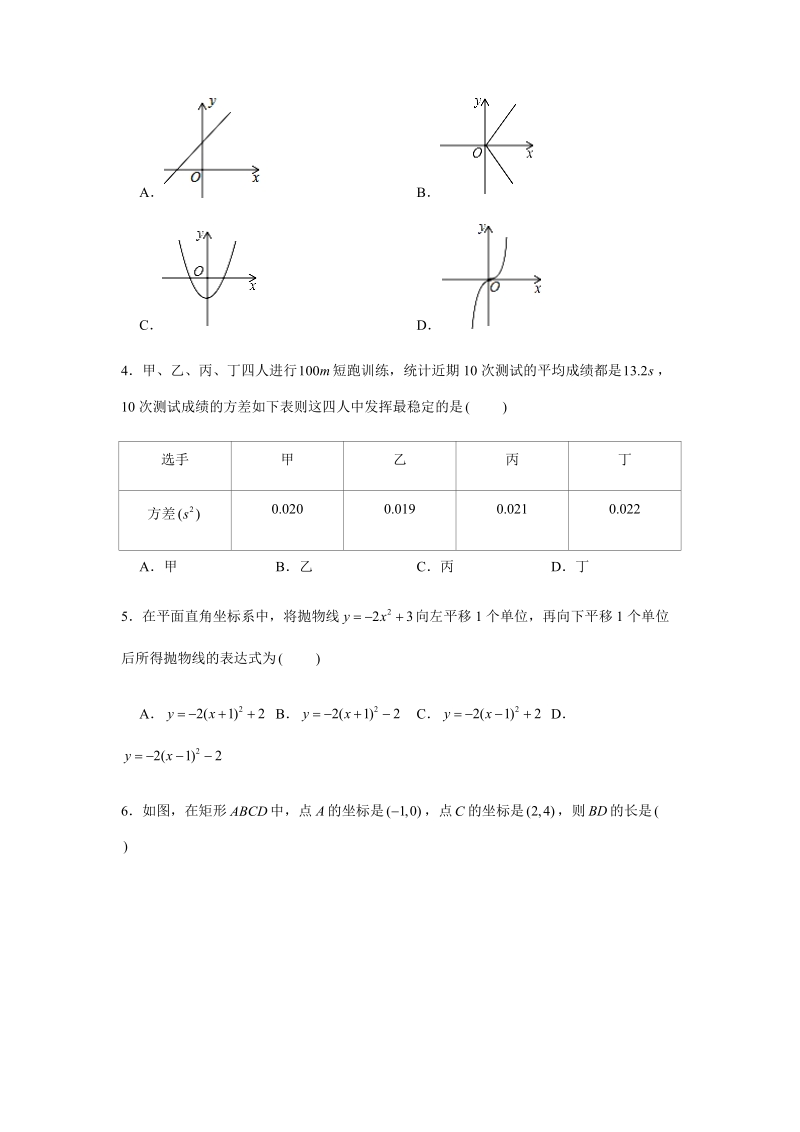
1、2019-2020学年北京市海淀区清华大学附中九年级(上)开学数学试卷一、选择题(本题共24分,每小题3分)1下列四组数,可作为直角三角形三边长的是A、B、C、D、2已知(如图,按图2图3所示的尺规作图痕迹,(不需借助三角形全等)就能推出四边形是平行四边形的依据是A两组对边分别平行的四边形是平行四边形B对角线互相平分的四边形是平行四边形C一组对边平行且相等的四边形是平行四边形D两组对边分别相等的四边形是平行四边形3下列各图象中,不是关于的函数图象的是ABCD4甲、乙、丙、丁四人进行短跑训练,统计近期10次测试的平均成绩都是,10次测试成绩的方差如下表则这四人中发挥最稳定的是选手甲乙丙丁方差0.
2、0200.0190.0210.022A甲B乙C丙D丁5在平面直角坐标系中,将抛物线向左平移1个单位,再向下平移1个单位后所得抛物线的表达式为ABCD6如图,在矩形中,点的坐标是,点的坐标是,则的长是A6B5CD72018年我国科技实力进一步增强,嫦娥探月、北斗组网、航母海试、鲲龙击水、港珠澳大桥正式通车,这些成就的取得离不开国家对科技研发的大力投入下图是2014年年我国研究与试验发展经费支出及其增长速度情况年我国研究与试验发展经费支出为19657亿元,比上年增长,其中基础研究经费1118亿元根据统计图提供的信息,下列说法中合理的是A2014年年,我国研究与试验发展经费支出的增长速度始终在增加B
3、2014年年,我国研究与试验发展经费支出增长速度最快的年份是2017年C2014年年,我国研究与试验发展经费支出增长最多的年份是2017年D2018年,基础研究经费约占该年研究与试验发展 经费支出的二、填空题(本题共24分,每小题3分)8如果关于的方程没有实数根,则的取值范围为9若直线下移后经过点,则平移后的直线解析式为10如图是二次函数图象的一部分,对称轴为直线,抛物线与轴的交点为、,则、两点的距离是11已知一组数据1,4,3,5,若它的平均数是3,则这组数据的中位数是12若二次函数的图象与轴交于,则的值是13如图,正方形的顶点,分别在轴,轴上,是菱形的对角线若,则点的坐标是14直线与直线在
4、同一平面直角坐标系中的图象如图所示,则关于的不等式的解集为15如图,的周长为17,点,在边上,的平分线垂直于,垂足为点,的平分线垂直于,垂足为点,若,则的长度为三、解答题16解方程:17如图,在中,垂足分别为,求证:18已知,求代数式的值19二次函数的图象经过点,(1)求、的值;(2)求该二次函数图象的顶点坐标和对称轴20已知关于的一元二次方程(1)证明:不论为何值时,方程总有实数根;(2)当为何整数时,方程有两个不相等的整数根21在直角坐标系中,已知一次函数的图象与轴交于点,交轴交于点(1)求,两点的坐标;(2)在给定的平面直角坐标系中画出该函数的图象;(3)根据图象回答:当时,的取值范围是
5、22如图,中,分别是,的中点(1)求证:四边形是菱形;(2)如果,求四边形的面积23有这样一个问题,探究函数的图象与性质,小张根据学习函数的经验,对函数的图象与性质进行了研究,下面是小张的探究过程,请补充完整:(1)函数的自变量取值范围是(2)下表是与的几组对应值:0123430003求的值;(3)如图,在平面直角坐标系中,算出了以上表中各对对应值为坐标的点,根据算出的点,画出该函数的图象;(4)进一步探究发现,该函数图象在第四象限内的最低点是,结合函数的图象,写出该函数的其他性质(一条即可);(5)根据图象回答:方程有个实数解24据北京晚报介绍自2009年故宫博物院年度接待观众首次突破100
6、0万人次之后,每年接待量持续增长,到2018年突破1700万人次,成为世界上接待量最多的博物馆,特别是随着我在故官修文物,上新了,故宫等一批电视文博节目的播出,社会上再次掀起故宫热于是故宫文创营销人员为开发针对不同年龄群体的文创产品,随机调查了部分参观故官的观众的年龄,整理并绘制了如下统计图表2018年参观故宫观众年龄频数分布直方图 年龄岁频数人数频率800.240350.17537合计2001000请根据图表信息回答下列问题:(1)求表中,的值;(2)补全频数分布直方图;(3)从数据上看,年轻观众已经成为参观故宫的主要群体,如果今年参观故宫人数达到2000万人次,那么其中年轻观众预计约有万人
7、次25在平面直角坐标系中,抛物线(1)求抛物线的对称轴(用含的代数式表示)(2)若点向右平移4个长度单位,得到点若抛物线经过点,求的值;抛物线与线段恰有一个交点,结合函数图象,直接写出的取值范围26四边形是正方形,是对角线,是平面内一点,且,过点作,且连接、,是的中点,作射线交于点(1)如图1,若点,分别在,边上求证:;(2)如图2,若点在四边形内,点在直线的上方,求与的和的度数27在平面直角坐标系中,为直线上一点,是直线外一点,且直线与轴不平行,若为某个矩形的对角线,且该矩形的边均与某条坐标轴垂直,则称该矩形为直线的“伴随矩形”如图为直线的“伴随矩形”的示意图(1)已知点在直线上,点的坐标为
8、若点的纵坐标为0,则以为对角线的直线的“伴随矩形”的面积是;若以为对角线的直线的“伴随矩形”是正方形,求直线的表达;(2)点在直线上,且点的纵坐标为4,若在以点,为顶点的四边形上存在一点,使得以为对角线的直线的“伴随矩形”为正方形,直接写出的取值范围2019-2020学年北京市海淀区清华大学附中九年级(上)开学数学试卷参考答案与试题解析一、选择题(本题共24分,每小题3分)1下列四组数,可作为直角三角形三边长的是A、B、C、D、【解答】解:、,此组数据不能构成直角三角形,故本选项错误;、,此组数据不能构成直角三角形,故本选项错误;、,此组数据不能构成直角三角形,故本选项错误;、,此组数据能构成
9、直角三角形,故本选项正确故选:2已知(如图,按图2图3所示的尺规作图痕迹,(不需借助三角形全等)就能推出四边形是平行四边形的依据是A两组对边分别平行的四边形是平行四边形B对角线互相平分的四边形是平行四边形C一组对边平行且相等的四边形是平行四边形D两组对边分别相等的四边形是平行四边形【解答】解:由图可知先作的垂直平分线,再连接的中点与点,并延长使,可得:,进而得出四边形是平行四边形,故选:3下列各图象中,不是关于的函数图象的是ABCD【解答】解:由函数的定义可知,每一个给定的,都有唯一确定的值与其对应的才是函数,故选项、中的函数图象都是关于的函数,中的不是,故选:4甲、乙、丙、丁四人进行短跑训练
10、,统计近期10次测试的平均成绩都是,10次测试成绩的方差如下表则这四人中发挥最稳定的是选手甲乙丙丁方差0.0200.0190.0210.022A甲B乙C丙D丁【解答】解:,方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好乙最稳定故选:5在平面直角坐标系中,将抛物线向左平移1个单位,再向下平移1个单位后所得抛物线的表达式为ABCD【解答】解:将抛物线向左平移1个单位,再向下平移1个单位,所得抛物线的函数表达式是:即故选:6如图,在矩形中,点的坐标是,点的坐标是,则的长是A6B5CD【解答】解:点的坐标是,点的坐标是,线段,四边形是矩形,故选:7201


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2019 2020 学年 北京市 海淀区 清华大学 附中 九年级 开学 数学试卷 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-108991.html