 鲁京津琼专用2020版高考数学大一轮复习第六章数列微专题七放缩法在证明中的应用课件
鲁京津琼专用2020版高考数学大一轮复习第六章数列微专题七放缩法在证明中的应用课件
《鲁京津琼专用2020版高考数学大一轮复习第六章数列微专题七放缩法在证明中的应用课件》由会员分享,可在线阅读,更多相关《鲁京津琼专用2020版高考数学大一轮复习第六章数列微专题七放缩法在证明中的应用课件(15页珍藏版)》请在七七文库上搜索。
微专题七 放缩法在证明中的应用,第六章 数列,解题策略 放缩法是不等式证明的重要方法,其中的放缩技巧既有模式可循但更有创意之变,如何灵活运用放缩法解题是衡量解题者思维好坏的标杆 常见的放缩形式有:,另外,利用重要不等式放缩、导数应用中有关ln x型的放缩(如:ln(1x)0)等也是常见的放缩方式 利用放缩法证明不等式的难点是放缩的“度”不好把握,放大了或放小了都得不出所证不等式,这样需要回头调整,留一项或几项不放缩逐步试验向所证结论靠扰,下面举例说明,又易知当n1,2,3时,不等式显然成立,


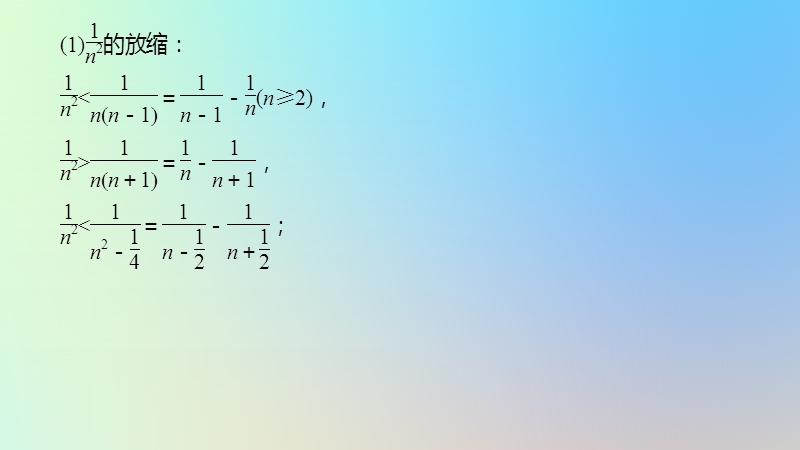
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 鲁京津琼 专用 2020 高考 数学 一轮 复习 第六 数列 专题 七放缩法 证明 中的 应用 课件
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-107050.html