1、 - 1 - 2019-2020 学年度秋四川省棠湖中学高三期中考试 理科数学试题理科数学试题 第第 I I 卷卷( (选择题选择题 共共 6060 分）分） 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分.在每个小题所给出的四个选项中，只 有一项是符合 题目要求的，把正确选项的代号填在答题卡的指定位置.） 1已知集合lg(1)Ax yx，1,0,1,2,3B ，则BA A1,0 B1,0,1 C1,2,3 D2,3 2若1()(1)aibii（, a bR，i 为虚数单位），则复数abi在复平面内对应的点所在的象限为 A第一象限 B第二象限 C第三象限 D第四象限 3已知实数
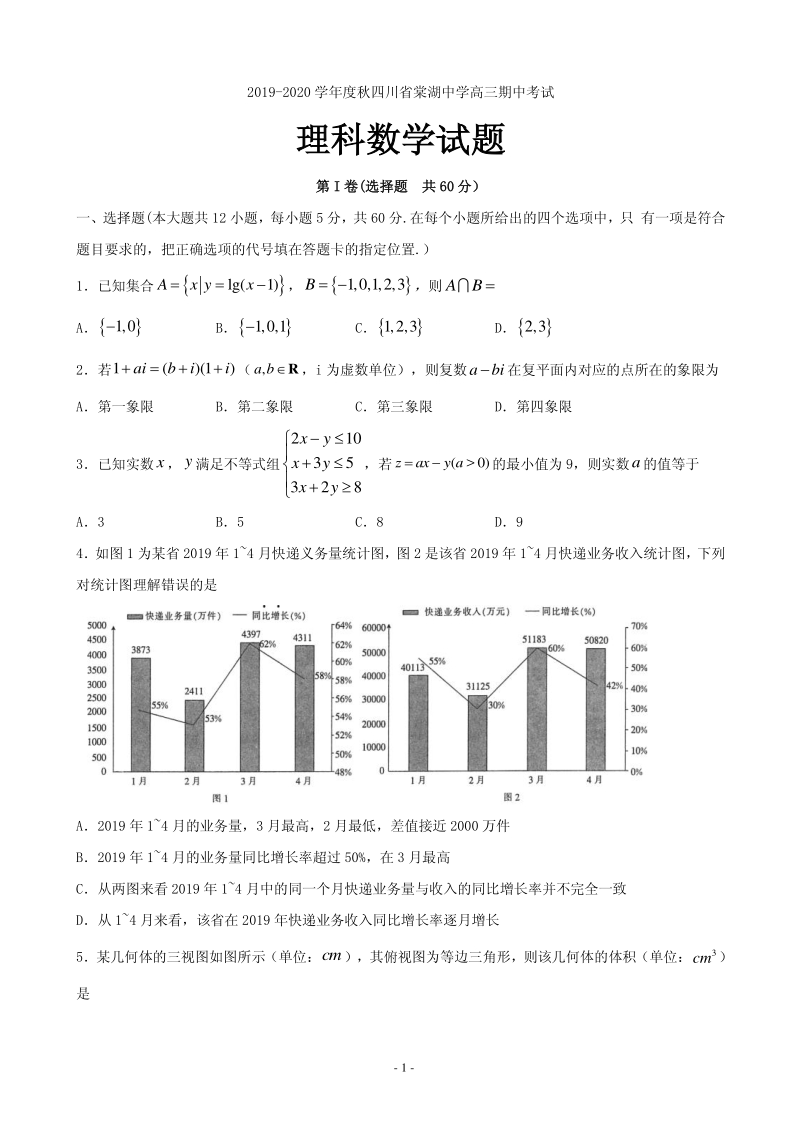
2、x，y满足不等式组 210 35 328 xy xy xy ，若 ( 0)zaxy a 的最小值为 9，则实数a的值等于 A3 B5 C8 D9 4如图 1 为某省 2019 年 14 月快递义务量统计图，图 2 是该省 2019 年 14 月快递业务收入统计图，下列 对统计图理解错误的是 A2019 年 14 月的业务量，3 月最高，2 月最低，差值接近 2000 万件 B2019 年 14 月的业务量同比增长率超过 50%，在 3 月最高 C从两图来看 2019 年 14 月中的同一个月快递业务量与收入的同比增长率并不完全一致 D从 14 月来看，该省在 2019 年快递业务收入同比增长率
3、逐月增长 5某几何体的三视图如图所示（单位：cm），其俯视图为等边三角形，则该几何体的体积（单位： 3 cm） 是 - 2 - A4 3 B 10 3 3 C2 3 D 8 3 3 6已知点(3, 2)P为双曲线 2 2 2 1 x y a 上一点，则它的离心率为 A. 3 2 B. 2 3 3 C.3 D.2 3 7设函数 3 f x2xa3 xsinxax，若 f x为奇函数，则曲线 yf x在点0,0处的切线方程 为 Ay x By2x Cy3x Dy4x 8已知正项等比数列 n a的前n项和为 n S，且 24 74SS，则公比q的值为 A1 B1或 1 2 C 3 2 D 3 2 9
4、十三届全国人大二次会议于2019年3月5日至15日在北京召开，会议期间工作人员将其中的5个代表 团人员（含A、B两市代表团）安排至a，b，c三家宾馆入住，规定同一个代表团人员住同一家宾馆， 且每家宾馆至少有一个代表团入住，若A、B两市代表团必须安排在a宾馆入住，则不同的安排种数为 A6 B12 C16 D18 10已知( )2sin()f xx同时满足下列三个条件： 12 4f xf x 时， 12 xx 的最小值为 2 3 yfx 是偶函数：(0) 6 ff 若 ( )f x在0, ) t有最小值，则实数t的取值范围可以是 A0, 6 B0, 3 C, 6 3 D; 3 2 11设圆锥曲线C
5、的两个焦点分别为 12 ,F F，若曲线C上存在点P满足 1122 :4:3:2PFFFPF ，则 曲线C的离心率等于 A. 1 2 或 3 2 B. 1 2 或 2 3 C. 1 2 D. 2 3 12不等式 3 ln1 x x eaxx 对任意 (1,)x恒成立，则实数a的取值范围 A(,1 e B 2 (,2e C(, 2 D(, 3 第第卷（非选择题共卷（非选择题共 9090 分）分） 二、填空题(本大题共 4 小题，每小题 5 分，满分 20 分） - 3 - 13已知向量3,4a ，1, r bk ，且a b ，则 4 r r ab 与a的夹角为_ 14已知 2 3 n x x 的
6、展开式中第 5 项为常数项，则该式中所有项系数的和为_. 15已知正三棱柱 111 ABCABC底面边长为2 3，高为 3，圆O是三角形ABC的内切圆，点P是圆O上 任意一点，则三棱锥 111 PABC的外接球的体积为_ 16已知直线l:y=k(x-2)与抛物线C:y 2=8x 交于A,B两点，F为抛物线C的焦点，若|AF|=3|BF|，则直线 l的倾斜角为_。 三、解答题（共三、解答题（共 7070 分，解答应写出文字说明、证明过程或演算步骤，第分，解答应写出文字说明、证明过程或演算步骤，第 17 2117 21 题为必考题，每个试题题为必考题，每个试题 考生都必须作答，第考生都必须作答，第
7、 2222、2323 题为选考题，考生根据要求作题为选考题，考生根据要求作答答. .） 17.（本大题满分 12 分） 每年七月份，我国 J 地区有 25 天左右的降雨时间，如图是 J 地区 S 镇 2000-2018 年降雨量（单位：mm）的 频率分布直方图，试用样本频率估计总体概率，解答下列问题： （）假设每年的降雨天气相互独立，求 S 镇未来三年里至少有两年的降雨量不超过 350mm 的概率； ()在 S 镇承包了 20 亩土地种植水果的老李过去种植的甲品种水果，平均每年的总利润为 31.1 万元而 乙品种水果的亩产量 m（kg/亩）与降雨量之间的关系如下面统计表所示，又知乙品种水果的单
8、位利润为 32-0.01m（元/kg），请帮助老李排解忧愁，他来年应该种植哪个品种的水果可以使利润 （万元）的 期望更大？（需说明理由）； 降雨量 100，200） 200，300） 300，400） 400，500） 亩产量 500 700 600 400 18（本大题满分 12 分） - 4 - 在ABC中，角A，B，C的对边分别是a，b，c，且3 cos23cosaCbcA （）求角A的大小；()若2a ，求ABC面积的最大值 19（本大题满分 12 分） 如图，在四棱锥PABCD中，PA平面ABCD，ABAD，ACCD，60ABC， PAABBC，E是PC的中点 （）求PB和平面PAD
9、所成的角的大小 ()求二面角APDC的正弦值 20（本大题满分 12 分） 已知椭圆 22 22 :1(0) xy Cab ab ， 3c ，左、右焦点为 12 ,F F，点 , ,P A B在椭圆C上，且点,A B关于原点对称，直线,PA PB的斜率的乘积为 1 4 . （）求椭圆C的方程； ()已知直线l经过点2,2Q，且与椭圆C交于不同的两点,M N，若 16 3 QM QN ，判断直线l的斜 率是否为定值？若是，请求出该定值；若不是，请说明理由. 21（本大题满分 12 分） 已知函数 1 ln2 x f xa xbeaxa （e为自然对数的底，a，b为常数且,Ra b） （）当0a
10、时，讨论函数 fx在区间1,上的单调性； ()当2b 时，若对任意的1x， 0f x 恒成立，求实数a的取值范围 （二）选考题：共（二）选考题：共 1010 分，请考生在第分，请考生在第 2222、2323 题中任选一题作答题中任选一题作答. .如果多做，则按所做的第一题计分如果多做，则按所做的第一题计分. . 22. 选修 4-4：坐标系与参数方程（10 分） 在直角坐标系xOy中，已知曲线 1 C的参数方程： 2 1 2 2 2 xt yt （t为参数），以坐标原点为极点，x轴正 - 5 - 半轴为极轴建立极坐标系，曲线 2 C的极坐标方程为2 sin(0) 4 aa . （）若曲线 1
11、C与曲线 2 C相切，求a的值； ()若曲线 1 C与曲线 2 C交于,A B两点，且| |6AB ，求a的值. 23已知, a b为正实数，函数( ) |2 |f xxaxb. （）求函数 ( )f x的最大值； ()若函数 ( )f x的最大值为 1，求 22 4ab的最小值. - 6 - 20192019- -20202020 学年度秋四川省棠湖中学高三期中考试学年度秋四川省棠湖中学高三期中考试 理科数学试题参考答案理科数学试题参考答案 1-5:DABDA 6-10:BCCBD 11-12:AD 13 4 14-32 15 20 5 3 16 3 或 2 3 17（1）频率分布直方图中第
12、四组的频率为1 1000.0020.0040.0030.1 该地区在梅雨季节的降雨量超过350mm的概率为50 0.0030.10.25 所以该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率为 23 23 33 111915 1 444646432 CC （或0.15625.） （2）据题意，总利润为20320.01nn元，其中500,700,600,400n . 所以随机变量（万元）的分布列如下表： 27 35 31.2 22.4 P 0.2 0.4 0.3 0.1 故总利润（万元）的期望 27 0.235 0.431.2 0.322.4 0.1E 5.4 14.09.362.
13、2431（万元） 因为3128，所以老李应该种植乙品种杨梅可使总利润（万元）的期望更大. 18：（）由正弦定理可得：3sin cos2sin cos3sin cosACBACA 从而可得：3sin2sin cosA CBA，即3sin2sin cosBBA 又B为三角形内角，所以sin0B ，于是 3 cos 2 A 又A为三角形内角，所以 6 A （）由余弦定理： 222 2cosabcbcA得： 22 3 4223 2 bcbcbcbc， 所以4 23bc ，所以 1 sin23 2 SbcA. 19解：（1）在四棱锥PABCD中，PA平面ABCD，AB平面ABCD， - 7 - PAAB
14、又ABAD，PAADA，AB平面PAD 故PB在平面PAD内的射影为PA，从而APB为PB和平面PAD所成的角 在Rt PAB中，ABPA，故45APB 所以PB和平面PAD所成的角的大小为45 （2）在四棱锥PABCD中，PA平面ABCD，CD平面ABCD，PACD 由条件ACCD，PAACA，CD 平面PAC 又AE 平面PAC，CDAE由PAABBC，60ABC，可得ACPA E是PC的中点，PCAE又CDPCC，AE 平面PCD 过点E作EMPD，垂足为M，连接AM，如图所示 AE 平面PCD，AM在平面PCD内的射影是EM， AMPDAME是二面角APDC的平面角 由已知30CAD，
15、设1CD ， 则3PAAC，2AD，6PC ，7PD RtPAC中， 16 22 AEPC 在Rt ADP中，AMPD，AM PDAP AD，得 2 21 7 AM 在Rt AEM中， 14 sin 4 AE AME AM 所以二面角APDC的正弦值为 14 4 20（1）由题意知： 2 2 1 4 PAPB b kk a ，又3c ， 222 abc - 8 - 可得： 2 4a ， 2 1b ， 2 3c 椭圆C的方程为： 2 2 1 4 x y （2）设直线l的方程为：22yk x 将其代入 2 2 1 4 x y，整理可得： 22 1416 (1)kxkk x 2 16(1)40k 则
16、 2 2 2 1614 1416 140kkkk ，得： 3 8 k 设 11 ,M x y， 22 ,N xy 则 12 2 161 1 4 k k xx k ， 22 12 22 4 483 16 14 1414 kk k x x kk 又 16 3 QM QN ，且,0QM QN 16 3 QM QN 又 11 2,2QMxy， 22 2,2QNxy 所以 1212 16 2222 3 xxyy 又 11 22yk x， 22 22yk x 22 1212121212 16 222222 1241 3 xxyyxxkx xxxk 2 2 22 4 483 16116 241 1 41 4
17、3 kk k k k kk 化简得： 2 2 16 1 16 143 k k ，解得： 2 2k 3 8 k 2k 直线l的斜率为定值 2 21（1）由题知0a 时， 1 2 x f xbex ， 1 2 x f xbe ，0x ， 当0b 时，得函数 fx在1,上单调递减； 当0b 时，由 0f x ，得 2 1xln b ，由 2 11ln b ，得2b ， .当02b时，函数 fx在区间 2 1,1ln b 上单调递减，在区间 2 1,ln b 上单调递增； .当2b 时，函数 fx在区间1,上单调递增 - 9 - （2）2b 时， 1 2e2 x f xalnxaxa ， 则 1 1
18、2e2 22 x x xaxaa f xea xx ， 由（1）知，函数 1 2e2 x yx 在区间1,上单调递增， 所以当1x 时， 10 2e22e20 x x ，即 1 exx ， 2 2221 xaxaxax f x xx 当2a 时， 0f x 在区间1，上恒成立，即 fx在1，上单调递增， 10f xf（合题意） 当2a 时， 由 2f xa ，得 1 2 2ex a fx x ，且 fx在1，上单调递增， 又10a ， 10 1 a ee ， 120fa， 1 210 a fae ， 故 fx在1,a上存在唯一的零点 0 x，当 0 1xx ，时， 0fx ， 即 f x在 0
19、 1,xx上递减，此时 10f xf，知 fx在 0 1,xx上递减， 此时 10f xf与已知矛盾（不合题意）， 综上：满足条件的实数a的取值范围是,2 22（1）直线 1 C的直角坐标方程为10xy 圆 2 C的普通方程为 22 2 22 22 xayaa 因为直线l与圆 2 C相切，所以 22 1 22 2 42 aa aa （2）把 1 C的参数方程： 2 1 2 2 2 xt yt （t为参数）代入曲线 2 C的普通方程： 得 2 2210tta ，故 121 2 2,21ttt ta ， - 10 - 2 12121 2 642ABttttt ta 23解：（1）因为 22f xxaxbab， 所以函数 fx的最大值为2ab. （2）由（1）可知，21ab， 因为 22 a4b4ab ， 所以()() 22222 2 a4ba4b4aba2b ， 所以 2 22 2421abab， 即 22 1 4 2 ab， 且当 1 2 2 ab时取“”， 所以 22 4ab的最小值为 1 2 .
