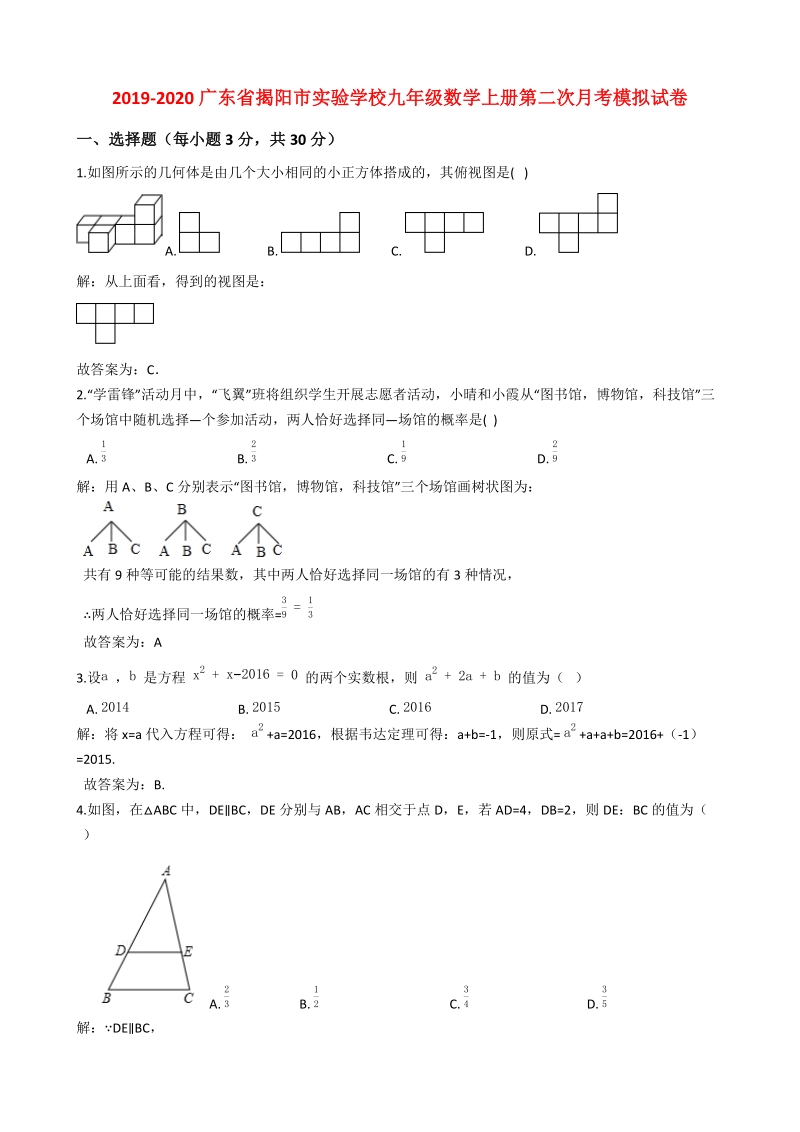
1、2019-2020广东省揭阳市实验学校九年级数学上册第二次月考模拟试卷一、选择题（每小题3分，共30分）1.如图所示的几何体是由几个大小相同的小正方体搭成的，其俯视图是( ) A.B.C.D.解：从上面看，得到的视图是： 故答案为：C2.“学雷锋”活动月中，“飞翼”班将组织学生开展志愿者活动，小晴和小霞从“图书馆，博物馆，科技馆”三个场馆中随机选择个参加活动，两人恰好选择同场馆的概率是( ) A.13B.23C.19D.29解：用A、B、C分别表示“图书馆，博物馆，科技馆”三个场馆画树状图为： 共有9种等可能的结果数，其中两人恰好选择同一场馆的有3种情况， 两人恰好选择同一场馆的概率=39=1
2、3 故答案为：A3.设a ，b 是方程 x2+x2016=0 的两个实数根，则 a2+2a+b 的值为（ ） A.2014B.2015C.2016D.2017解：将x=a代入方程可得： a2 +a=2016，根据韦达定理可得：a+b=-1，则原式= a2 +a+a+b=2016+（-1）=2015. 故答案为：B.4.如图，在ABC中，DEBC，DE分别与AB，AC相交于点D，E，若AD=4，DB=2，则DE：BC的值为（ ） A.23B.12C.34D.35解：DEBC， ADEABC，DEBC=ADAB=ADAD+DB=46=23.故答案为：A.5.如图，两张等宽的纸条交叉重叠在一起，重叠
3、的部分为四边形ABCD， 若测得A， C之间的距离为6cm， 点B，D之间的距离为8cm，则线段AB的长为（ ） A.5 cm B.4.8 cm C.4.6 cmD.4 cm解：作ARBC于R，ASCD于S，连接AC、BD交于点O 由题意知：ADBC，ABCD，四边形ABCD是平行四边形，两个矩形等宽，AR=AS，ARBC=ASCD，BC=CD，平行四边形ABCD是菱形，ACBD，在RtAOB中，OA=3，OB=4，AB= 32+42 =5，故答案为：A6.如图，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF.把纸片展平，再一次折叠纸片，使点A落在EF上的点A处，并使折痕经过点B，得到折
4、痕BM.若矩形纸片的宽AB=4，则折痕BM的长为( ) A.833B.433C.8D.83解：对折矩形纸片ABCD，使AD与BC重合，AB=4， BE= 12 AB=2，BEF=90，把纸片展平，再一次折叠纸片，使点A落在EF上的点A处，并使折痕经过点B，AB=AB=4，BAM=A=90，ABM=MBA，EAB=30，EBA=60，ABM=30，在RtABM中，AB=BM cosABM，即4=BM cos30，解得：BM= 833 ，故答案为：A.7.某测量队在山脚A处测得山上树顶仰角为45（如图），测量队在山坡上前进600米到D处，再测得树顶的仰角为60，已知这段山坡的坡角为30，如果树高为
5、15米，则山高为（ ）（精确到1米， 3 1.732）. A.585米B.1014米C.805米D.820米解：过点D作DFAC于F, 在直角ADF中,AF=ADcos30=300 3 米,DF= 12 AD=300米,设FC=x,则AC=300 3 +x,在直角BDE中,BE= 3 DE= 3 x,则BC=300+ 3 x,在直角ACB中,BAC=45,这个三角形是等腰直角三角形,AC=BC,300 3 +x=300+ 3 x,解得:x=300,BC=AC=300+300 3 ,山高是300+300 3 -15=285+300 3 805（米）,故答案为：C.8.如图，已知点A是一次函数y2
6、x的图象与反比例函数y kx 的图象在第一象限内的交点，ABx轴于点B，点C在x轴的负半轴上，且ACBOAB，OAB的面积为4，则点C的坐标为（ ） A.（8，0）B.（6，0）C.（ 112 ，0）D.（ 92 ，0）解：A在直线y2x上， 设AB2x，OBx，OAB的面积为4， 12 x2x4，解得：x2，AB4，OB2，ABOB，ABOABO90，ACBOAB，AOBCAB， ABBC OBAB ， 42+OC 24 ，OC6，即C的坐标是（6，0），故答案为：B.9.已知二次函数yax2bxc的图象如图所示，有以下结论：abc0；abc0；2ab；4a2bc0；若点(2，y1)和( 1
7、3 ，y2)在该图象上，则y1y2. 其中正确的结论个数是 ( ) A.1个B.2个C.3个D.4个解：抛物线开口向下， a0，对称轴x= -b2a 0，b0，abc0，故不正确；对称轴x= -b2a =1，b=2a，令x=1时，此时y=ab+c，由图象可知ab+c0，故正确；当x1时，y随着x的增大而增大，2 13 ，y 1 0,x0) ， y2=2kx(xk2x 的 x 的取值范围； （2）求这两个函数的表达式； （3）点 P 在线段 AB 上，且 SAOP:SBOP=1:2 ，求点 P 的坐标. （1）解：观察图象可知当 x1 或 0x k2x（2）解：把 A(1,4) 代入 y=k2x
8、 ，得 k2=4 ， y=4x ，点 B(4,n) 在 y=4x 上， n=1 ， B(4,1) ，把 A(1,4) ， B(4,1) 代入 y=k1x+b1 得k1+b=44k1+b=1 ，解得 k1=1b=3 ， y=x+3 （3）解：设 AB 与 y 轴交于点 C ， 点 C 在直线 y=x+3 上， C(0,3) ，SAOB=12OC(|xA|+|xB|)=123(1+4)=7.5 ，又 SAOD:SBOP=1:2 ， SAOP=137.5=2.5 ， SBOP=5 ，又 SAOC=1231=1.5 ，点 P 在第一象限， SCOP=2.51.5=1 ，又 OC=3 ， 123xP=1
9、 ，解得 xP=23 ，把 xP=23 代入 y=x+3 ，得 yP=73 ， P(23,73) .五解答题（每小题10分，共24分）24.如图，在平面直角坐标系中，抛物线y=x2+ax+b交x轴于A（1，0），B（3，0）两点，点P是抛物线上在第一象限内的一点，直线BP与y轴相交于点C （1）求抛物线y=x2+ax+b的解析式； （2）当点P是线段BC的中点时，求点P的坐标； （3）在（2）的条件下，求sinOCB的值 （1）解：将点A、B代入抛物线y=x2+ax+b可得， ，解得，a=4，b=3，抛物线的解析式为：y=x2+4x3（2）解：点C在y轴上， 所以C点横坐标x=0，点P是线段B
10、C的中点，点P横坐标xP= = ，点P在抛物线y=x2+4x3上，yP= 3= ，点P的坐标为（ ， ）（3）解：点P的坐标为（ ， ），点P是线段BC的中点， 点C的纵坐标为2 0= ，点C的坐标为（0， ），BC= = ，sinOCB= = = 25.如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A（0，2）和C（2 3 ，0），点D是对角线AC上一动点（不与A，C重合），连结BD，作DEDB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF（1）填空：点B的坐标为_；（2）是否存在这样的点D，使得DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请
11、说明理由；（3）求证： DEDB = 33 ；设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用的结论），并求出y的最小值（1）（2 3 ，2）（2）解：存在理由如下：连接BE，取BE的中点K，连接DK、KCBDE=BCE=90，KD=KB=KE=KC，B、D、E、C四点共圆，DBC=DCE，EDC=EBC，tanACO= AOOC = 33 ，ACO=30，ACB=60如图1中，DEC是等腰三角形，观察图象可知，只有ED=EC，DBC=DCE=EDC=EBC=30，DBC=BCD=60，DBC是等边三角形，DC=BC=2，在RtAOC中，ACO=30，OA=2，AC=2AO=
12、4，AD=ACCD=42=2当AD=2时，DEC是等腰三角形如图2中，DCE是等腰三角形，易知CD=CE，DBC=DEC=CDE=15，ABD=ADB=75，AB=AD=2 3 ，综上所述，满足条件的AD的值为2或2 3（3）解：由（2）可知，B、D、E、C四点共圆，DBC=DCE=30，tanDBE= DEDB ， DEDB = 33 如图2中，作DHAB于H在RtADH中，AD=x，DAH=ACO=30，DH= 12 AD= 12 x，AH= AD2DH2 = 32 x，BH=2 3 32 x，在RtBDH中，BD= BH2+DH2 = (12x)2+(2332x)2 ，DE= 33 BD= 33 (12x)2+(2332x)2 ，矩形BDEF的面积为y= 33 (12x)2+(2332x)2 2= 33 （x26x+12），即y= 33 x22 3 x+4 3 ，y= 33 （x3）2+ 3 ， 33 0，x=3时，y有最小值 3 解：（1）四边形AOCB是矩形，BC=OA=2，OC=AB=2 3 ，BCO=BAO=90，B（2 3 ，2）故答案为（2 3 ，2）
